Механика грунтов КР. Механика грунтов

• Название: Механика грунтов
• Дата: 07.11.2021
• Размер: 1.25 Mb.
• Имя файла: Механика грунтов КР.doc
• Тип: Задача; #265153
• страница: 5 из 5

Задача №7. Деформации грунтов и прогноз осадок фундаментов

Равномерно распределенная полосообразная (ширина полосы b) нагрузка интенсивностью Р приложена на глубине h от горизонтальной поверхности слоистой толщи грунтов. Определить по методу послойного суммирования с учетом только осевых сжимающих напряжений величину полной стабилизированной осадки грунтов. С поверхности залегает песчаный грунт (мощностью h₁плотностью грунта ρ₁, плотностью частиц грунта ρ_S1, природной влажностью W₁, модулем общей деформации Е₀₁), подстилаемый водонепроницаемой глиной (h₂; ρ₂; Е₂). Уровень грунтовых вод расположен в слое песчаного грунта на расстоянии h_w от уровня подстилающего слоя.

Исходные данные:

b = 240 см; h = 130 см; Р = 0.38 МПа; h₁ = 320 см; ρ₁ = 1.98 г/см³; ρ_S1 = 2.65 г/см³;

W₁ = 0,124; Е₀₁ = 24 МПа; h₂ = 760 см; ρ₂ = 2.01 г/см³; Е₂ = 28 МПа; h_w = 160 см

Решение:

Величина полной стабилизированной осадки грунтовой толщи S определяется как сумма осадок элементарных слоев грунта по формуле: , где

β = 0,8;

σ_zpi – среднее значение дополнительного вертикального нормального напряжения:

;

h_i - толщина i-го слоя грунта;

E_i – модуль упругости i-го слоя;

n – число слоев.

, где α – коэффициент, принимаемый по таблице в зависимости от относительной глубины .

Нижняя граница снимаемой толщи основания принимается на глубине z = Hc, где выполняется условие , где - вертикальное напряжение от собственного веса грунта на уровне подошвы полосы нагрузки.

Строим график максимальных нормальных сжимающих напряжений, предварительно определив значения соответствующих параметров σ.

Сжимающее напряжение σ определяется по формуле , где Р – интенсивность приложенной нагрузки.

α₁ = 0,791 при z₁ = 1,3 м

α₂ = 0,623 при z₂ = 2,0 м

α₃ = 0,455 при z₃ = 3,0 м

α₄ = 0,346 при z₄ = 4,0 м

α₅ = 0,273 при z₅ = 5,0 м

α₆ = 0,219 при z₆ = 6,0 м

α₇ = 0,174 при z₇ = 7,0 м

α₈ = 0,161 при z₈ = 7,6 м

α₉ = 0,149 при z₉ = 8,0 м

α₁₀ = 0,126 при z₁₀ = 9,0 м

α₁₁ = 0,106 при z₁₁ = 10,0 м

α₁₂ = 0,095 при z₁₂ = 10,8 м

Определим напряжение для каждой из глубин

σ₁ = 0,301 при z₁ = 1,3 м

σ₂ = 0,237 при z₂ = 2,0 м

σ₃ = 0,173 при z₃ = 3,0 м

σ₄ = 0,131 при z₄ = 4,0 м

σ₅ = 0,104 при z₅ = 5,0 м

σ₆ = 0,083 при z₆ = 6,0 м

σ₇ = 0,066 при z₇ = 7,0 м

σ₈ = 0,061 при z₈ = 7,6 м

σ₉ = 0,057 при z₉ = 8,0 м

σ₁₀ = 0,048 при z₁₀ = 9,0 м

σ₁₁ = 0,040 при z₁₁ = 10,0 м

σ₁₂ = 0,036 при z₁₂ = 10,8 м

Определим вертикальное напряжение от собственного веса грунта на уровне подошвы полосы нагрузки 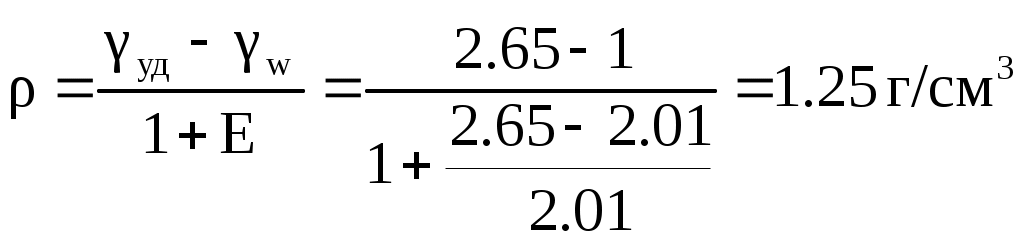по формуле: , где ρ – плотность песка с водой





Проверим, выполняется ли условие: . В нашем случае (0.036  0.04) это условие выполняется, значит, нижнюю глубину принимаем по глубине z = H =10,8 м.

Вычислим величину полной стабилизированной осадки грунтовой толщи S как сумму осадок элементарных слоев грунта по формуле: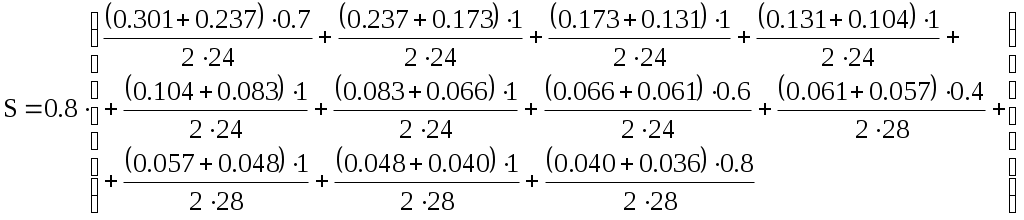

Задача №8. Деформации грунтов и прогноз осадок фундаментов

Равномерно распределенная в пределах квадратной площадки 200×200 нагрузка интенсивностью P = 0,24 МПа приложена к слою суглинка (мощность h₁ = 230 см, коэффициент относительной сжимаемости m_v1 = 0,176 МПа^-1, коэффициент фильтрации k_ф1 = 2,2·10^-8 см/с), подстилаемому глиной (мощность h₂ = 390 см, коэффициент относительной сжимаемости m_v2 = 0,284 МПа^-1, коэффициент фильтрации k_ф2 = 4,1·10^-9 см/с). Определить по методу эквивалентного слоя величину полной стабилизированной осадки грунтов, изменение осадки грунтов во времени в условиях одномерной задачи теории фильтрационной консолидации, построить график стабилизации осадки вида S = f(t). При определении значения коэффициента эквивалентного слоя Aω_const (для абсолютно жестких фундаментов) коэффициент относительной поперечной деформации для сжимаемой толщи грунтов можно принять υ = 0,3.

Решение:

При слоистой толще грунтов, для расчета осадки по методу эквивалентного слоя грунт приводится к квазиоднородному (на основе теорем о среднем коэффициенте относительной сжимаемости и о среднем коэффициенте фильтрации). В этом случае величина полной стабилизированной осадки S может быть определена по формуле:

,

где h_э – толщина эквивалентного слоя грунта;

m_vm – средний коэффициент относительной сжимаемости грунта;

Р – давление на грунт по подошве площадки.

Толщина эквивалентного слоя грунта h_э определяется по формуле:

,

где Аω – коэффициент эквивалентного слоя грунта, принимаемый для абсолютно жесткого фундамента (в соответствии с таблицей для квадратной площадки нагружения при значении υ = 0,3 величина Аω = 1,08);

b – наименьшая сторона площадки нагружения.

Таким образом, толщина эквивалентного слоя грунта h_э равна:

см.

Средний коэффициент относительной сжимаемости m_vm определяется по формуле:

,

где h_i – толщина отдельных слоев грунта до глубины ;

m_vi – коэффициент относительной сжимаемости i-го грунта;

Z_i – расстояние от точки, соответствующей глубине Н, до середины рассматриваемого i-го слоя грунта.

Находим средний коэффициент относительной сжимаемости m_vm: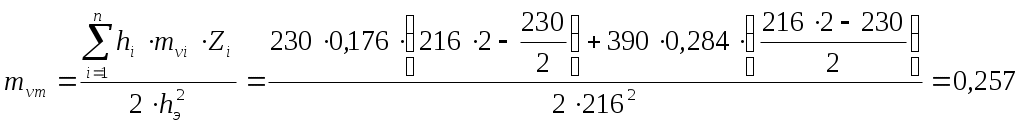

.

Величина полной стабилизированной осадки Sбудет равна:

см.

Осадка грунтовой толщи S_t для любого промежутка времени t определяется следующим выражением:

,

где S – полная стабилизированная осадка;

U – степень консолидации (уплотнения).

Выполнение степени консолидации U можно с достаточной для практических целей точностью выполнить по формуле:

,

где e – основание натуральных логарифмов;

N – коэффициент, зависящий от условий отвода вытесняемой из грунта воды;

,

где с_vm – коэффициент консолидации, в данном случае:

,

где k_фm – средний коэффициент фильтрации: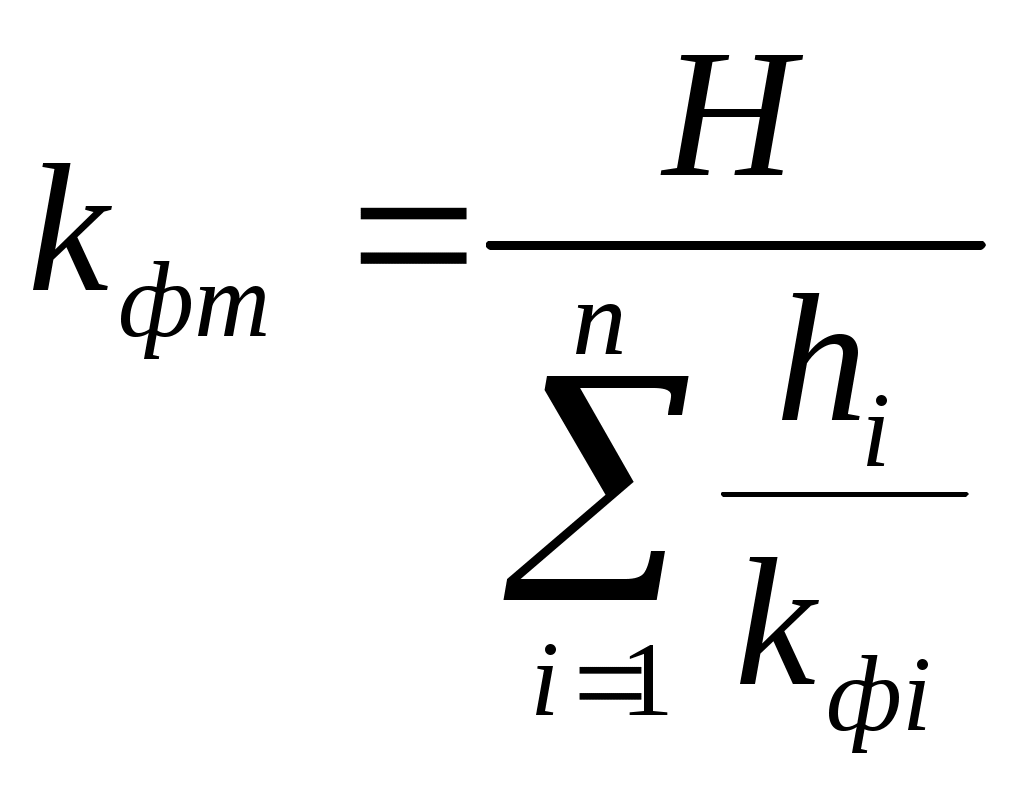

,

где k_фi – коэффициент фильтрации i-го слоя грунта;

ρ_w – плотность воды.

Найдем средний коэффициент фильтрации: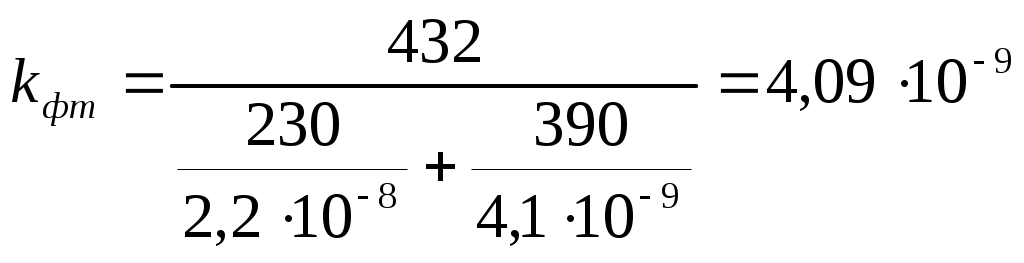

см/с.

Используя найденное значение, найдем коэффициент консолидации, учитывая, что 1 см/с ≈ 3·10⁷ см/год:

см²/год.

Тогда



Для вычисления t используем таблицу значений N для вычисления осадок грунта как функции времени:

	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
N	0,02	0,08	0,17	0,31	0,49	0,71	1,00	1,40	2,09	∞
t, лет	0,003	0,012	0,026	0,048	0,076	0,110	0,155	0,218	0,325	∞

Рис. 8-1. График изменения осадки во времени

Список использованных источников и литературы

1. 
   ГОСТ 25100-95. Грунты. Классификация.
   
2. 
   Деавльтовский Е.Э. Механика грунтов: Методические указания. – Ухта: УГТУ. 2000. – 46 с., ил.
   
3. 
   Цытович Н.А. Механика грунтов (краткий курс): Учебник для строит. вузов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1983. – 288 с., ил.