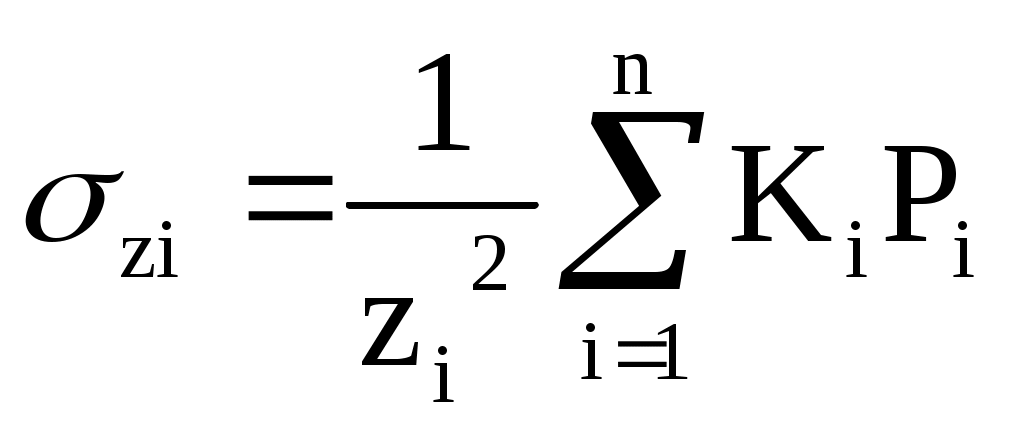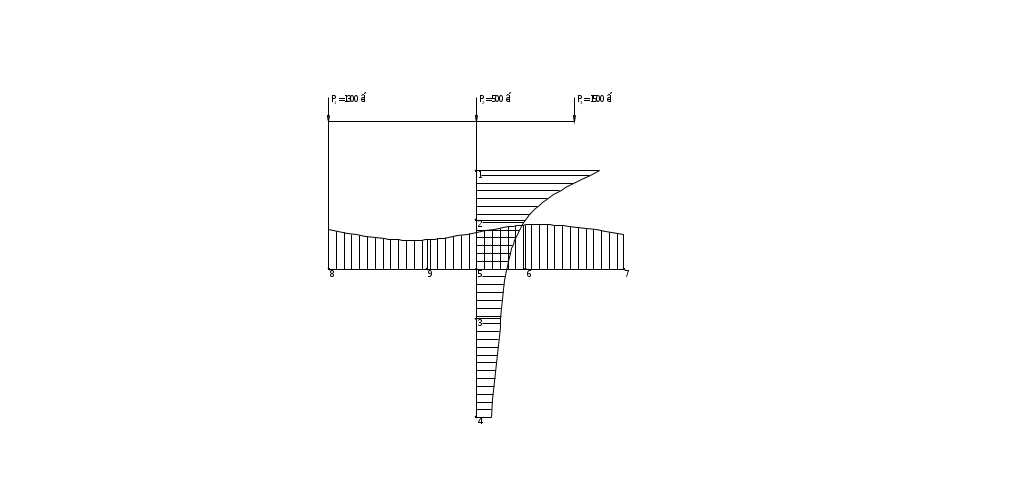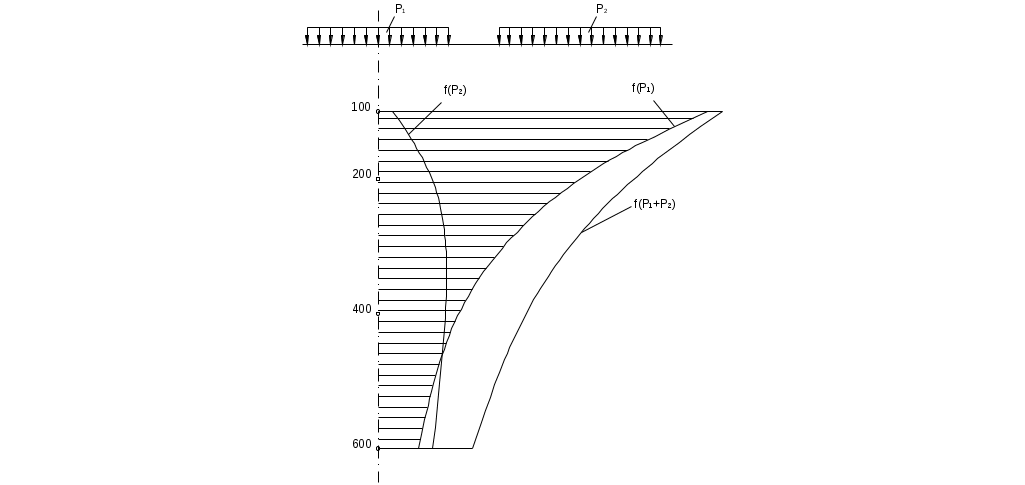Исходные данные:
К горизонтальной поверхности массива грунта приложено несколько
сосредоточенных сил:
Р1 = 1300 кН, Р2 = 500 кН, Р3 = 1500 кН
На расстоянии от рассматриваемой точки: r1 = 300 см, r2 = 200 см;
Глубина рассматриваемой точки от плоскости приложения сил: z = 300 см
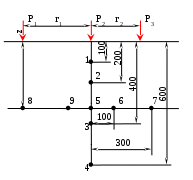
Рис. 2-1. Расчетная схема
Решение:
Для случая, когда к горизонтальной поверхности массива грунта приложено несколько сосредоточенных сил, величины вертикальных составляющих напряжений σzi, в любой точке массива грунта можно определить суммированием составляющих напряжений от действия каждой силы в отдельности с использованием зависимости:
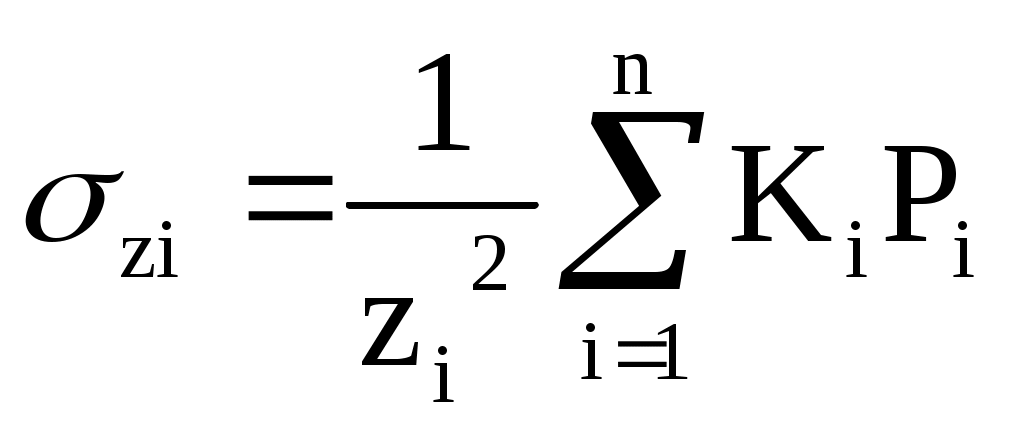
σz1 = 1/1002×(0,0015×1300+0,4775×500+0,0085×1500) = 0,0254 кН = 0,25 МПа
σz2 = 1 /2002×(0,0251 × 1300+0,4775 × 500+0,0844× 1500) = 0,0099 кН = 0,10 МПа
σz3 = 1/4002×(0,1565×1300+0,4775×500+0,2733× 1500) = 0,0053 кН = 0,05 МПа
σz4 = 1/6002×(0,2733×1300+0,4775×500+0,3687×1500) = 0,0032 кН = 0,03 МПа
σ z5 = 1/3002×(0,0844×1300+0,4775×500+0,1889×1500) = 0,007 кН = 0,07 МПа
σ z6 = 1/3002×(0,0374×1300+0,3687×500+0,3687×1500) = 0,0087 кН = 0,09 МПа
σz7 = 1/3002×(0,0085× 1300+0,0844×500+0,3687×1500) = 0,0067 кН = 0,07 МПа
σz8 = 1/3002×(0,4775×1300+0,0844×500+0,0171×1500) = 0,0077 кН = 0,08 МПа
σz9 = 1 /3002×(0,1889× 1300+0,3687×500+0,0844×1500) = 0,0062 кН = 0,06 МПа
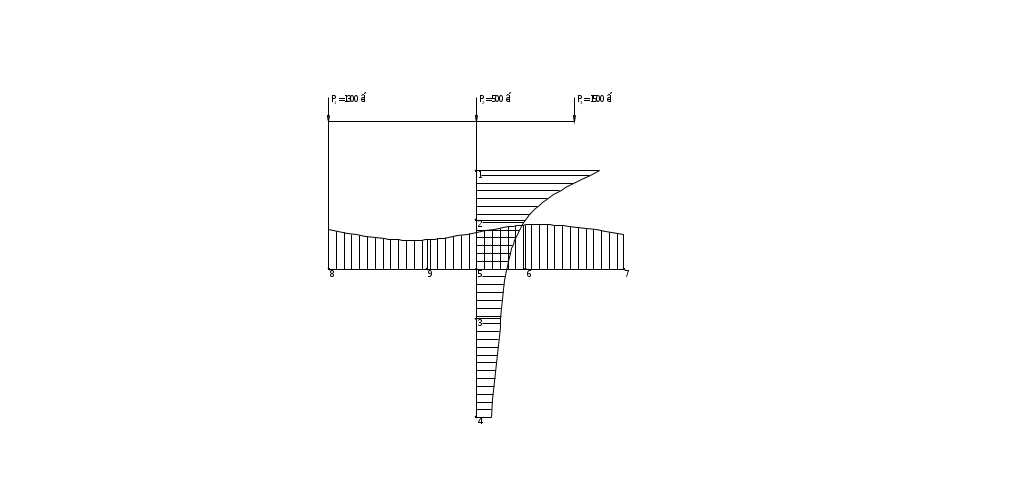
Рис. 2-2. Эпюры распределения вертикальных напряжений σz
Задача №3. Напряжения в грунтах от действия внешних сил
Исходные данные:
Горизонтальная поверхность массива грунта по прямоугольным плитам с размерами в плане 260×210 и 500×240 (размеры в сантиметрах) нагружена равномерно распределенной вертикальной нагрузкой интенсивностью 0,34 МПа и 0,38 МПа соответственно. Определить величины вертикальных составляющих напряжений σZ от совместного действия внешних нагрузок в точках массива грунта для заданной вертикали, проходящей через одну из точек М1, М2, М3 на плите №1. Расстояние между осями плит нагружения – 300 см. Точки по вертикали расположить от поверхности на расстоянии 100, 200, 400, 600 см. По вычисленным напряжениям построить эпюры распределения σZ (от каждой нагрузки отдельно и суммарную).
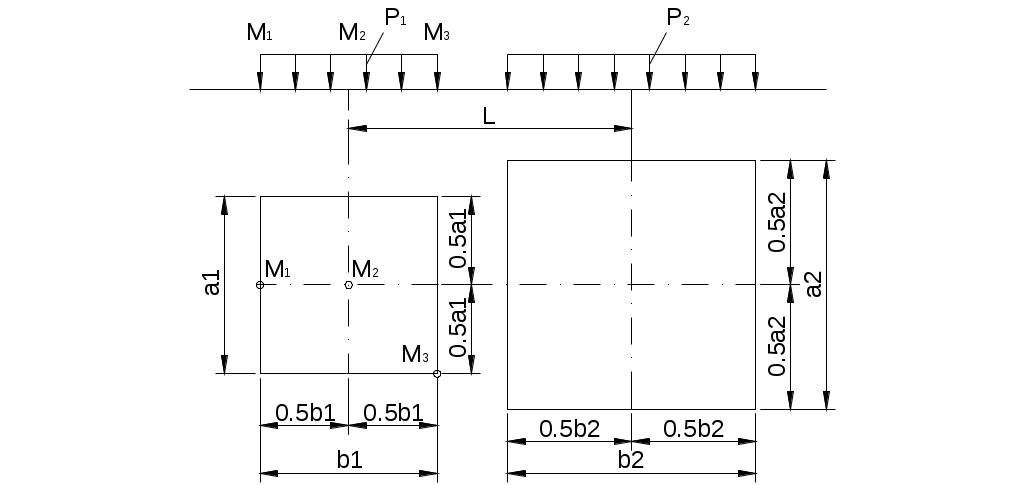
Рис. 3-1. Расчетная схема
Решение:
Используя метод угловых точек определение вертикальных составляющих напряжений в точке проводится по формуле:
Для площадок под центром загружения прямоугольника: 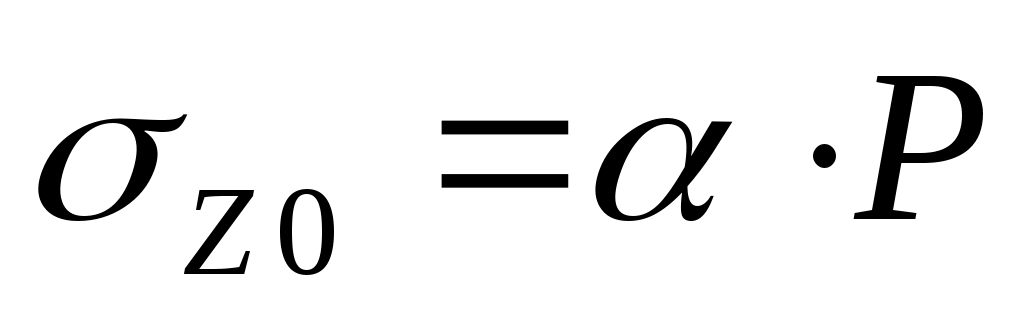 , где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения , где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения 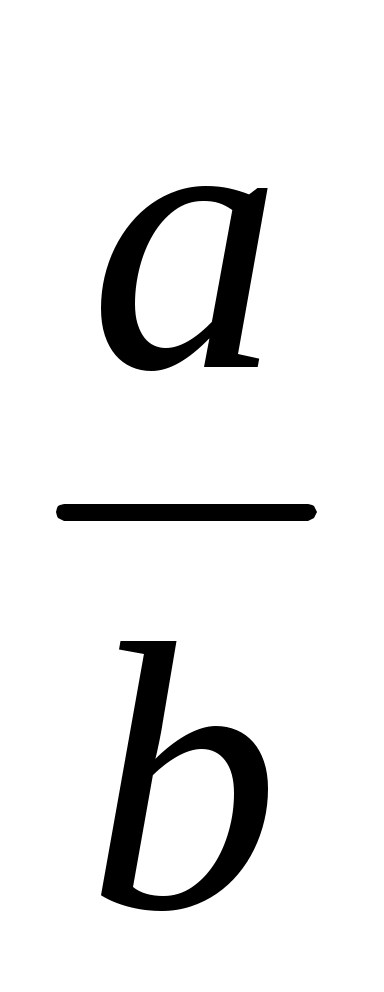 (а – длинная ее сторона, b – ее ширина) и отношения (а – длинная ее сторона, b – ее ширина) и отношения 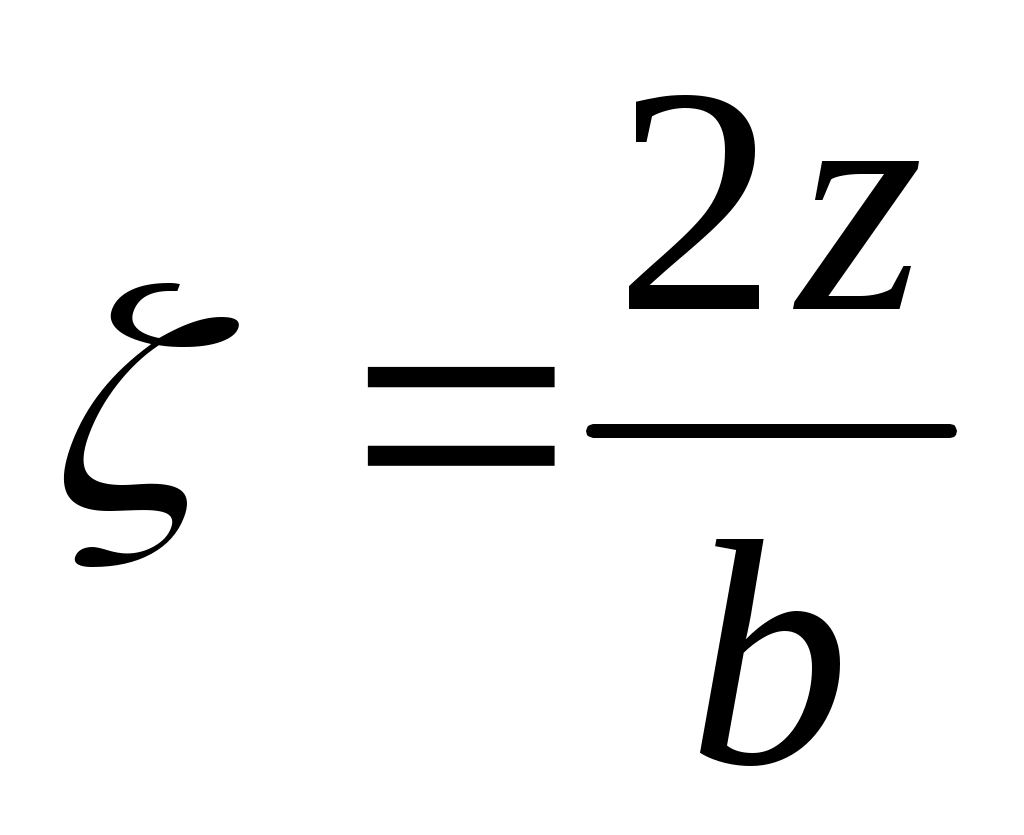 (z – глубина, на которой определяется напряжение (z – глубина, на которой определяется напряжение 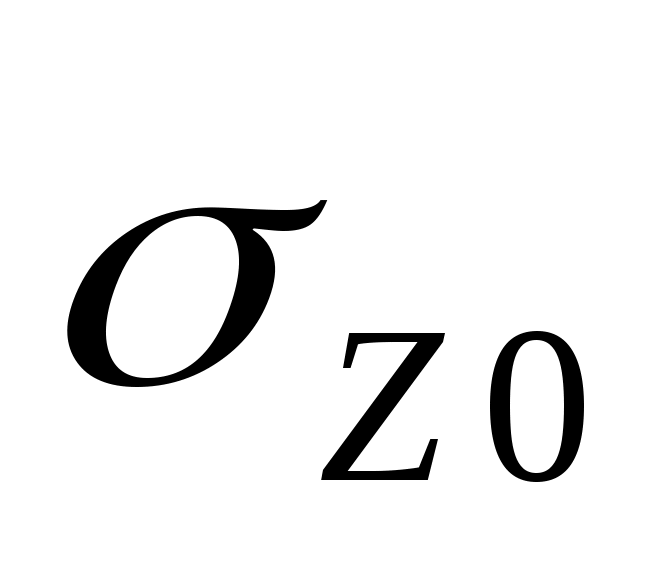 ), P – интенсивность равномерно распределенной нагрузки. ), P – интенсивность равномерно распределенной нагрузки.
Для площадок под углом загруженного прямоугольника: 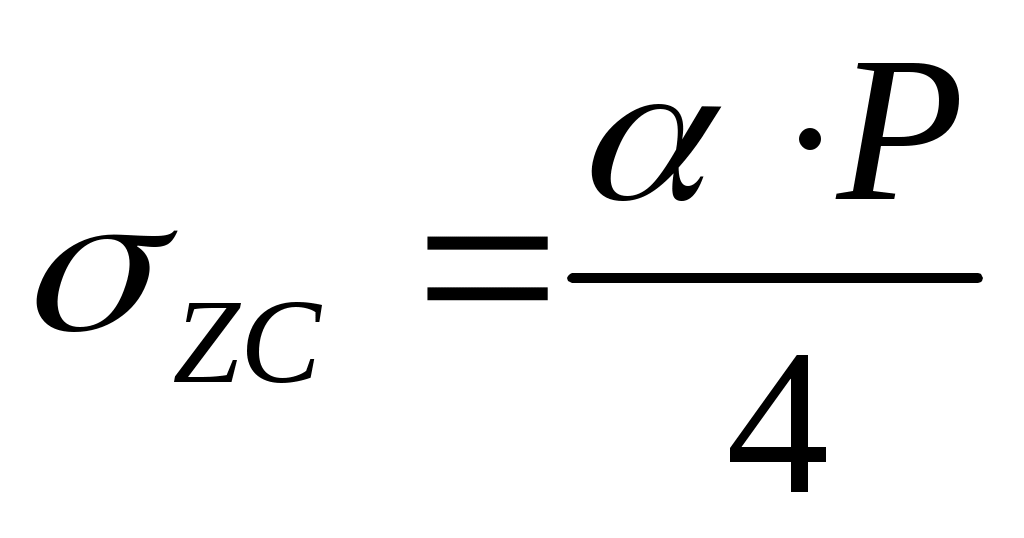 , где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения , где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения 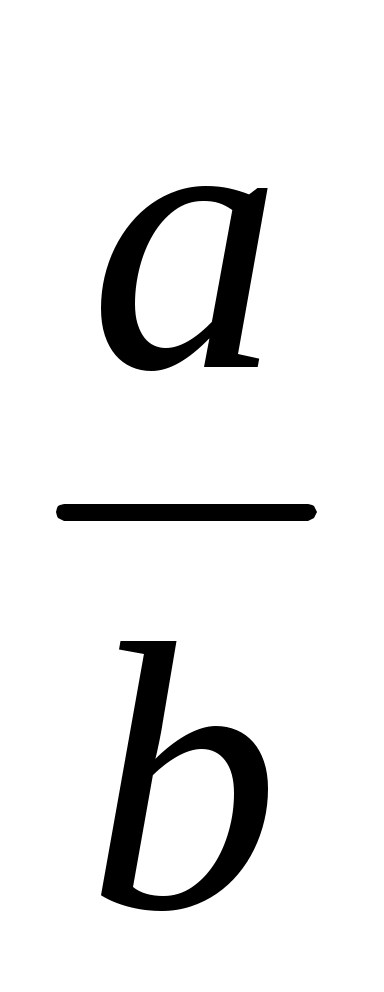 (а – длинная ее сторона, b – ее ширина) и отношения (а – длинная ее сторона, b – ее ширина) и отношения 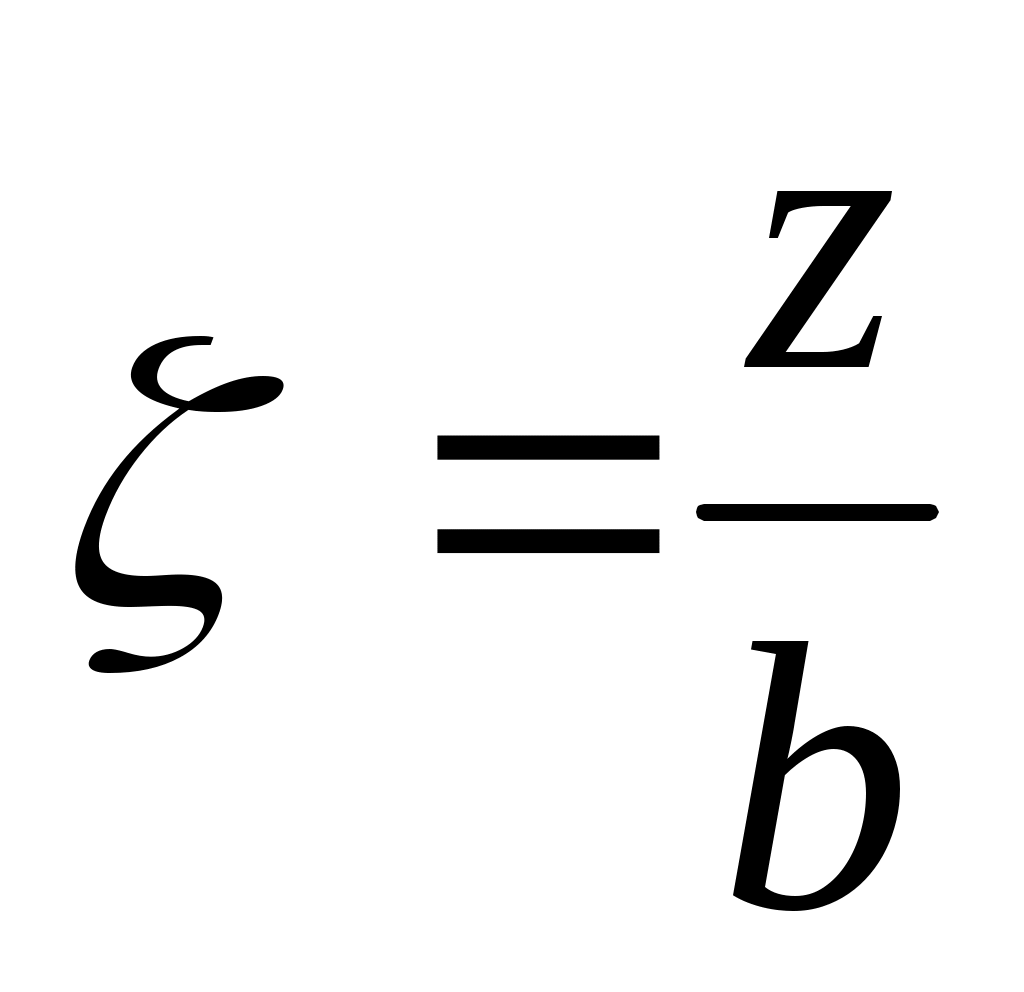 (z – глубина, на которой определяется напряжение (z – глубина, на которой определяется напряжение 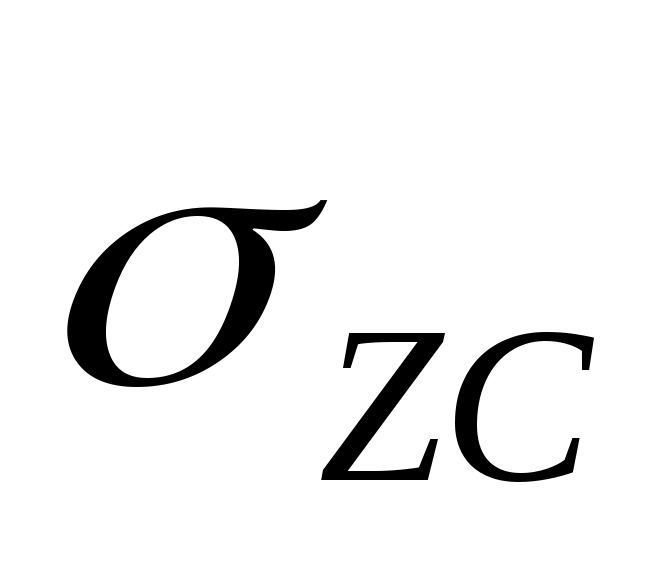 ), P – интенсивность равномерно распределенной нагрузки. ), P – интенсивность равномерно распределенной нагрузки.
Рассмотрим плиту №1.
а) Определим величину вертикальных составляющих напряжений в точке М1.
Разделим плиту на две составляющие таким образом, чтобы М1 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: 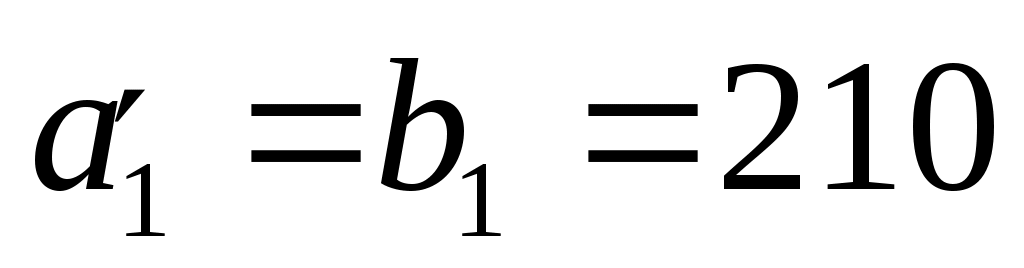 см, см, 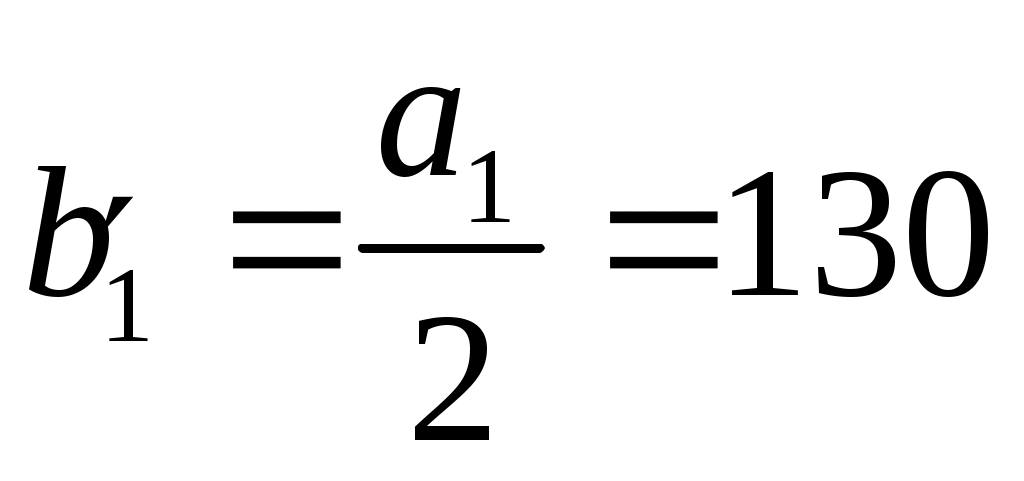 см. см.
Для глубины 100 см: 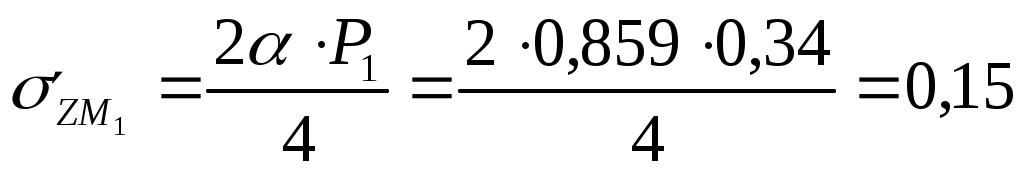 МПа МПа
Для глубины 200 см: 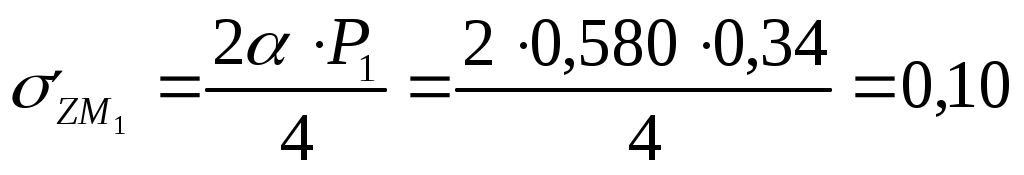 МПа МПа
Для глубины 400 см: 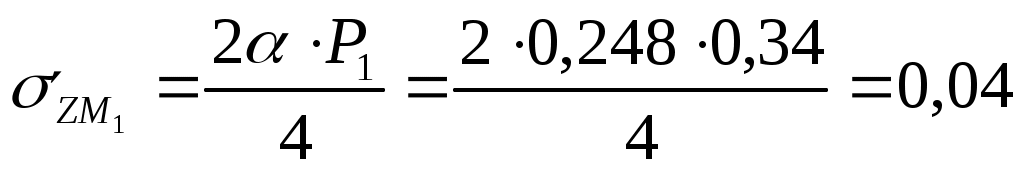 МПа МПа
Для глубины 600 см: 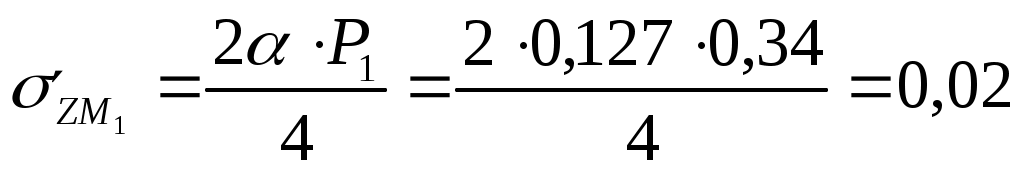 МПа МПа
б) Определим величину вертикальных составляющих напряжений в точке М2.
Поскольку М2 находится под центром плиты, применяем формулы для центра загружения:
Для глубины 100 см: 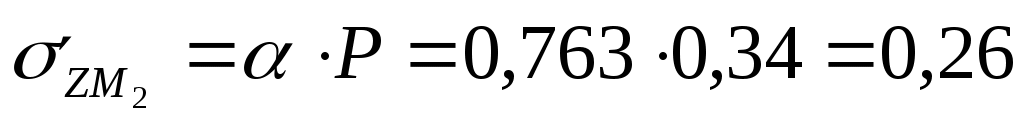 МПа МПа
Для глубины 200 см: 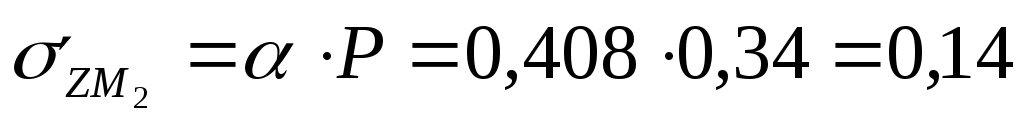 МПа МПа
Для глубины 400 см: 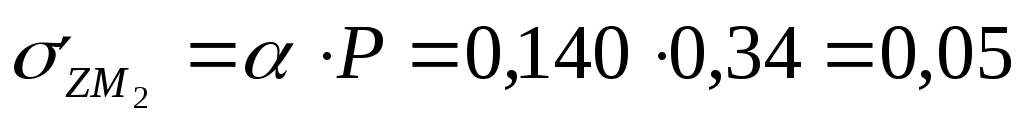 МПа МПа
Для глубины 600 см: 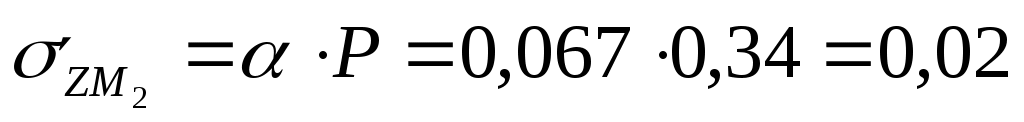 МПа МПа
в) Определим величину вертикальных составляющих напряжений в точке М3.
Для глубины 100 см: 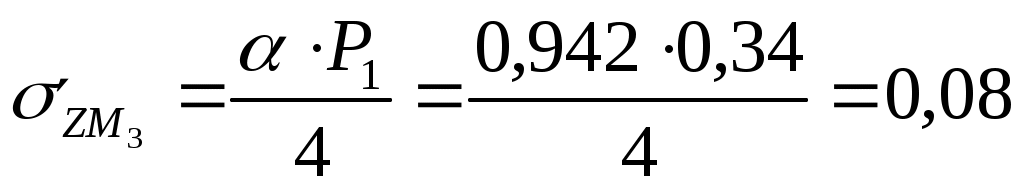 МПа МПа
Для глубины 200 см: 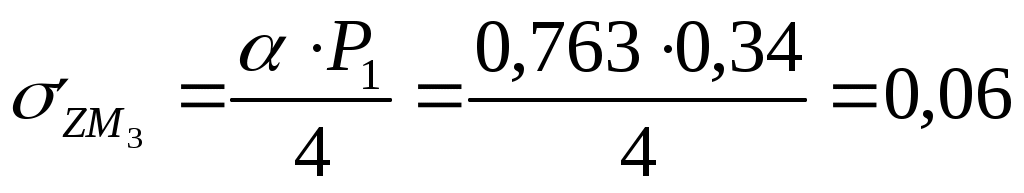 МПа МПа
Для глубины 400 см: 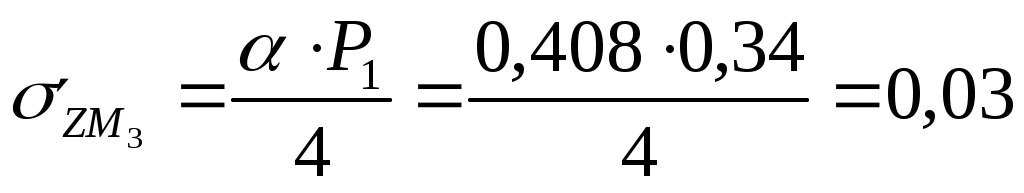 МПа МПа
Для глубины 600 см: 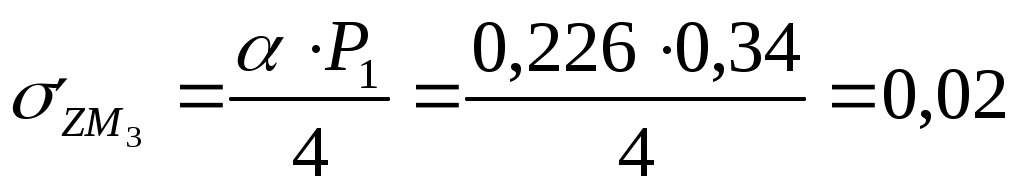 МПа МПа
Рассмотрим плиту №2
Поскольку точки М находятся вне прямоугольника давлений, величина 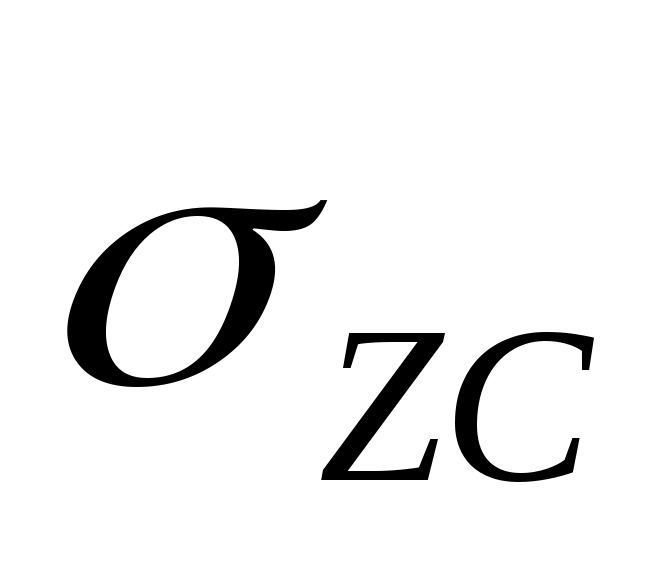 складывается из суммы напряжений от действия нагрузки по прямоугольникам под площадью давления, взятых со знаком «плюс», и напряжений от действия нагрузок по прямоугольникам вне площади давления, взятых со знаком «минус», т.е. складывается из суммы напряжений от действия нагрузки по прямоугольникам под площадью давления, взятых со знаком «плюс», и напряжений от действия нагрузок по прямоугольникам вне площади давления, взятых со знаком «минус», т.е.
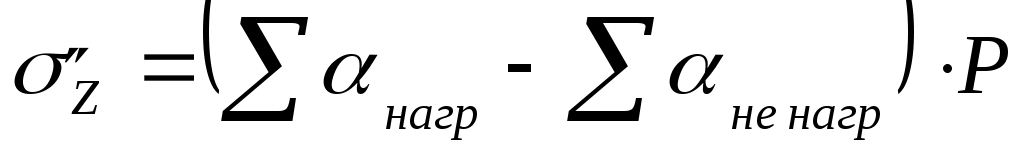 . .
а) Определим величину вертикальных составляющих напряжений в точке М1.
Разделим плиту на две составляющие таким образом, чтобы М1 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: 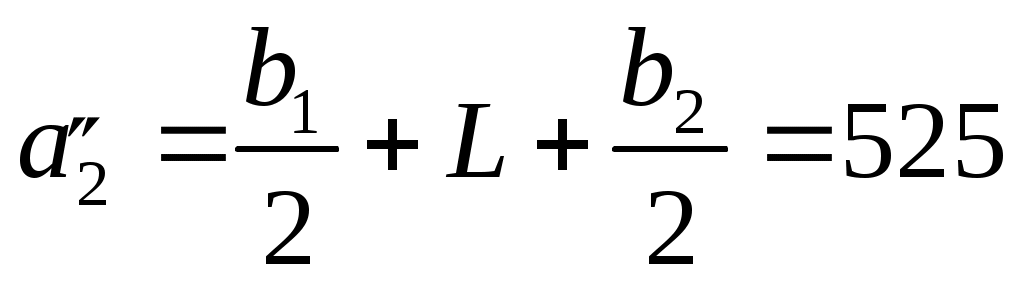 см, см, 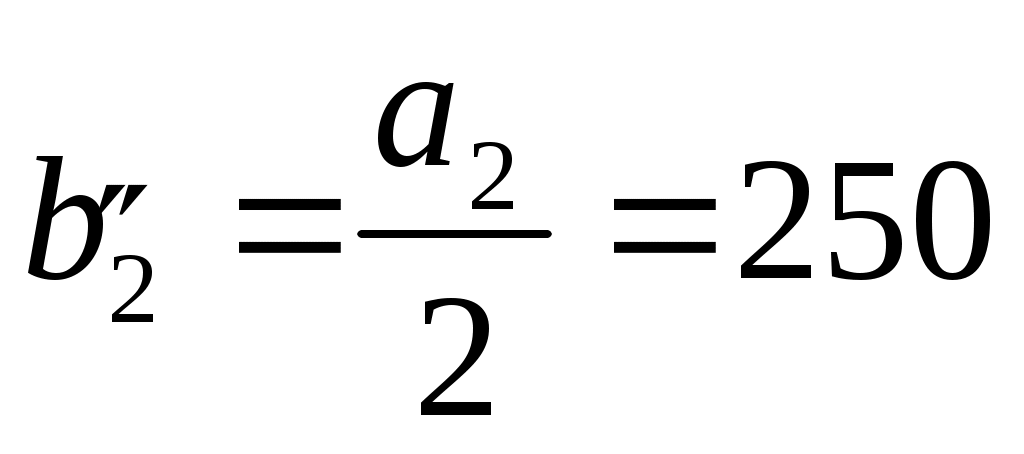 см. см.
Для глубины 100 см: 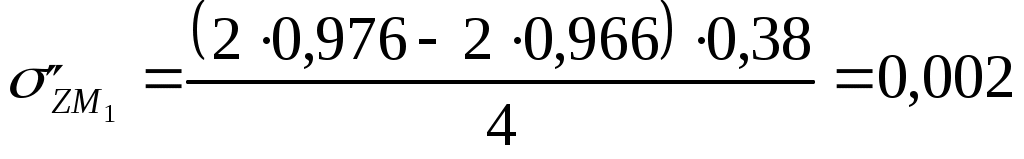 МПа МПа
Для глубины 200 см: 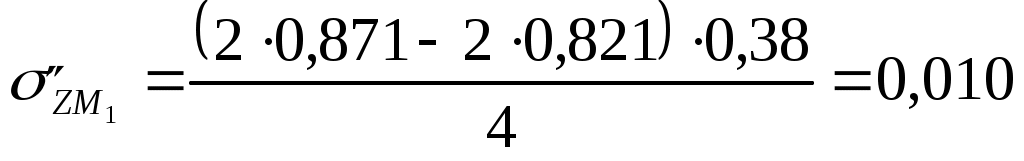 МПа МПа
Для глубины 400 см: 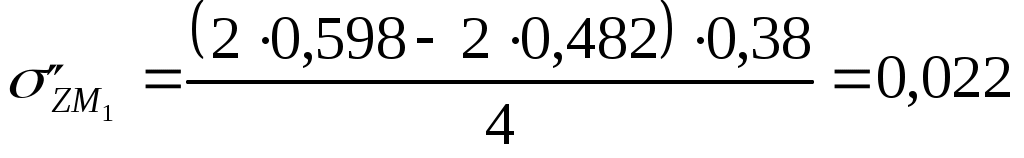 МПа МПа
Для глубины 600 см: 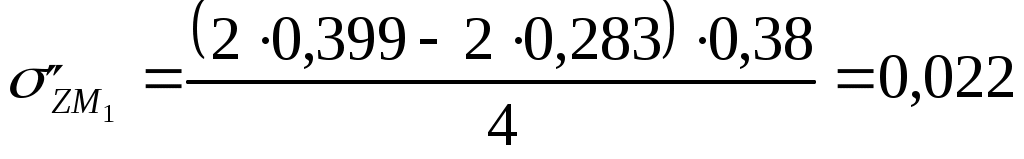 МПа МПа
б) Определим величину вертикальных составляющих напряжений в точке М2.
Разделим плиту на две составляющие таким образом, чтобы М2 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: 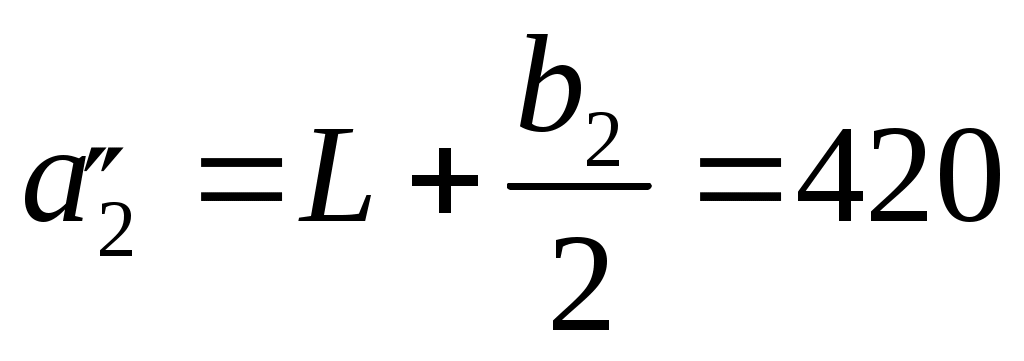 см, см, 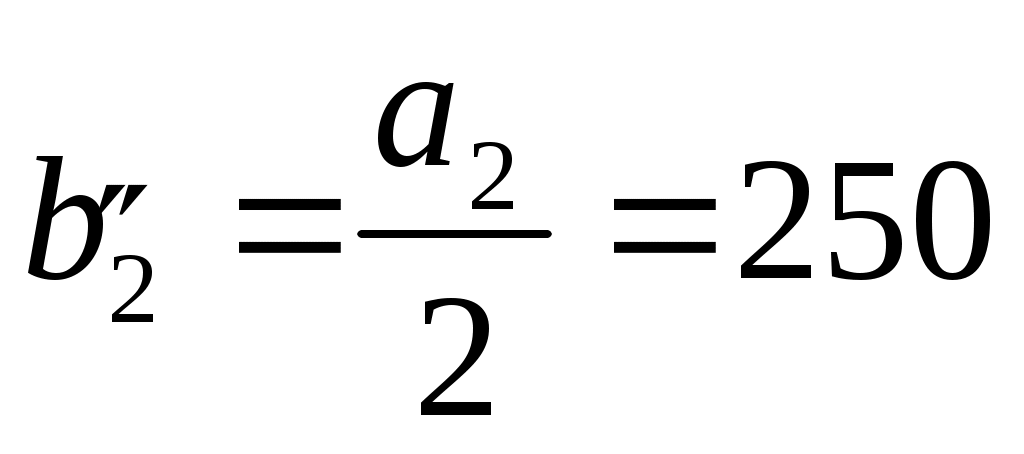 см. см.
Для глубины 100 см: 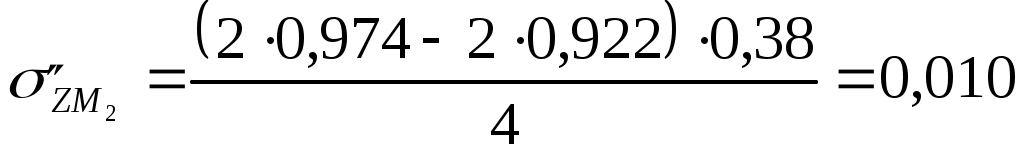 МПа МПа
Для глубины 200 см: 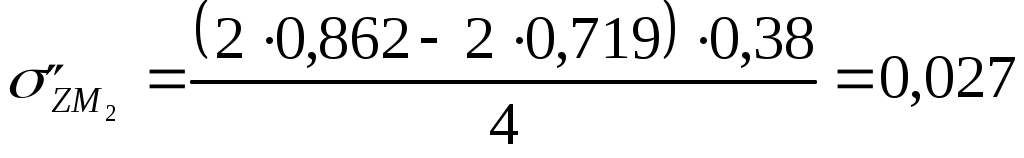 МПа МПа
Для глубины 400 см: 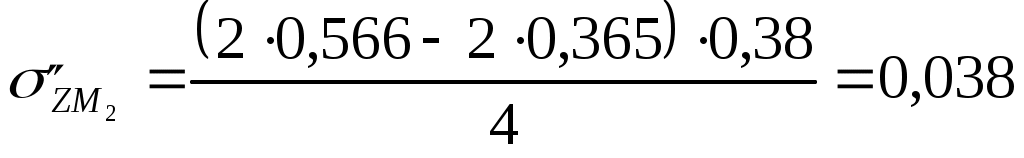 МПа МПа
Для глубины 600 см: 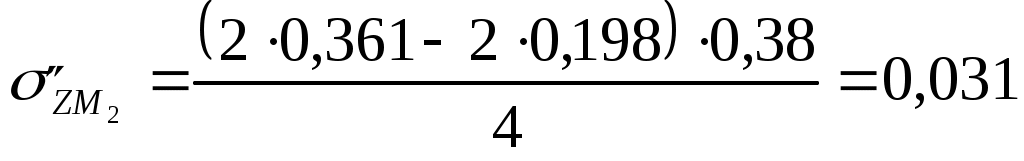 МПа МПа
в) Определим величину вертикальных составляющих напряжений в точке М3.
Разделим плиту на две составляющие таким образом, чтобы М3 являлась углом длинной стороны прямоугольников. Получатся два прямоугольника, причем верхний со сторонами: 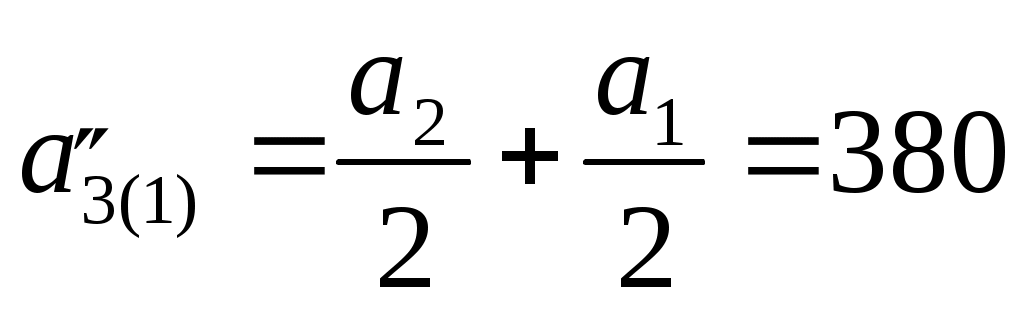 см, см, 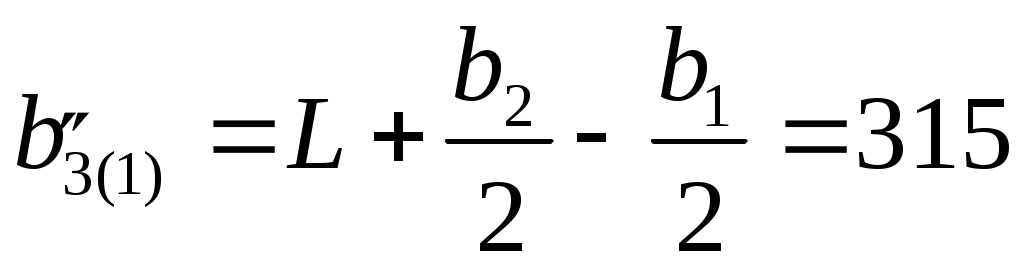 см; нижний – см; нижний – 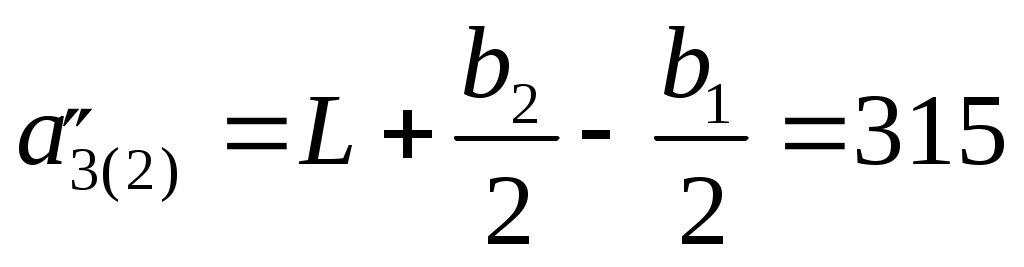 см, см, 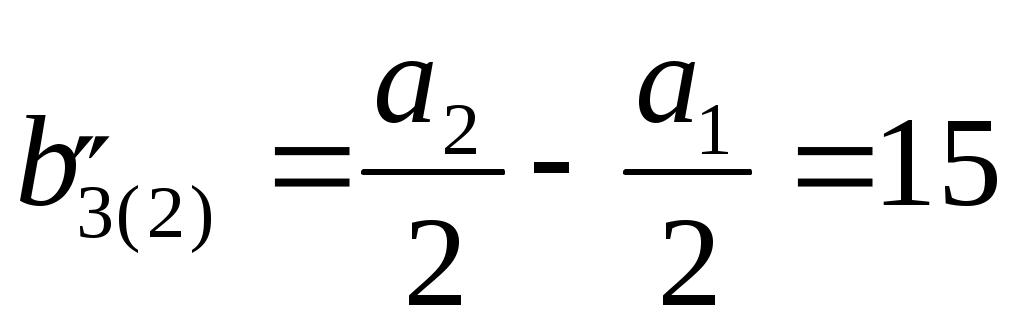 см. см.
Для глубины 100 см: 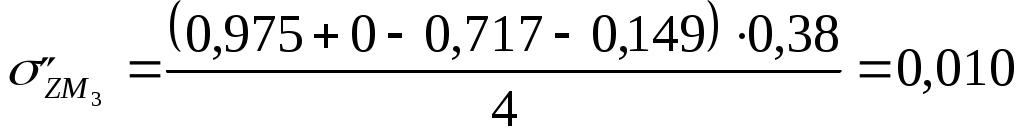 МПа МПа
Для глубины 200 см: 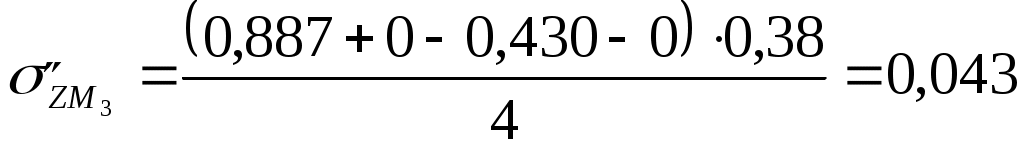 МПа МПа
Для глубины 400 см: 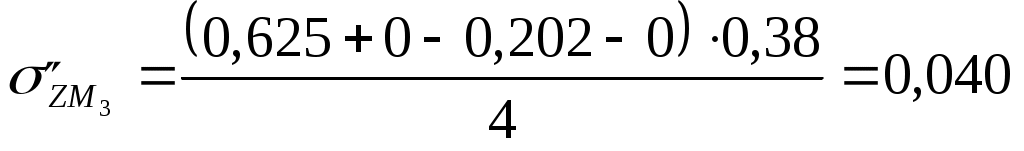 МПа МПа
Для глубины 600 см: 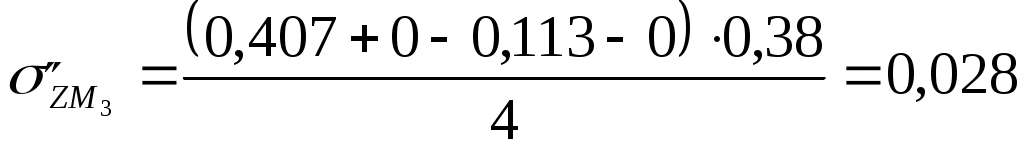 МПа МПа
Пользуясь принципом независимости действия сил, находим алгебраическим суммированием напряжения в заданных точках массива грунта.
Для действия распределенной нагрузки Р1:
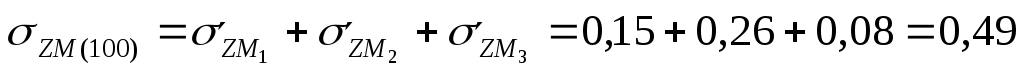 МПа МПа
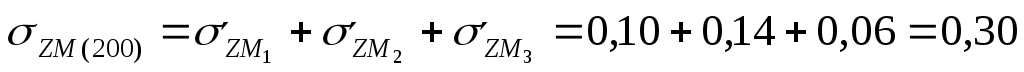 МПа МПа
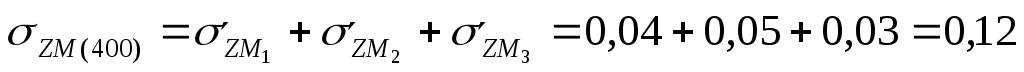 МПа МПа
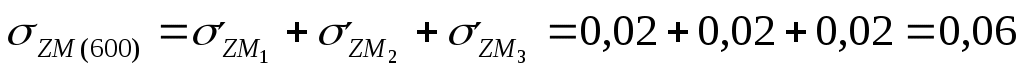 МПа МПа
Для действия распределенной нагрузки Р2:
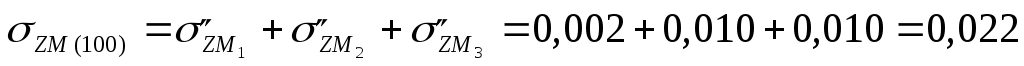 МПа МПа
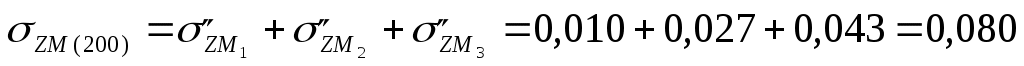 МПа МПа
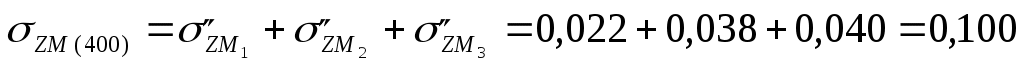 МПа МПа
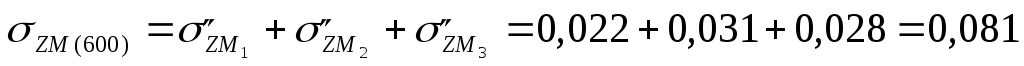 МПа МПа
Для действия суммарной нагрузки:
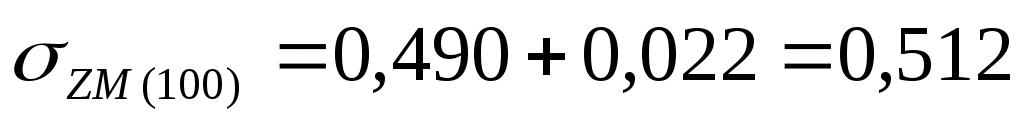 МПа МПа
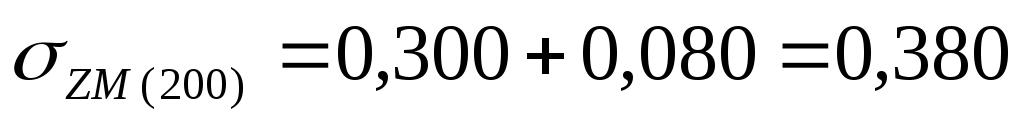 МПа МПа
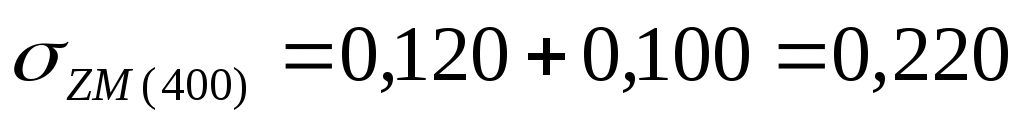 МПа МПа
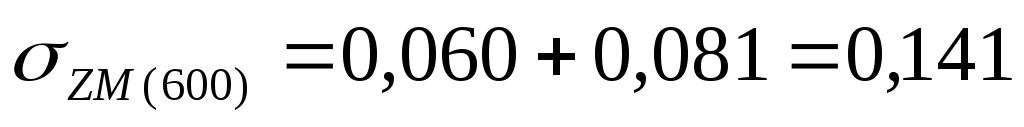 МПа МПа
На основании проведенных расчетов строим эпюры распределения σZ.
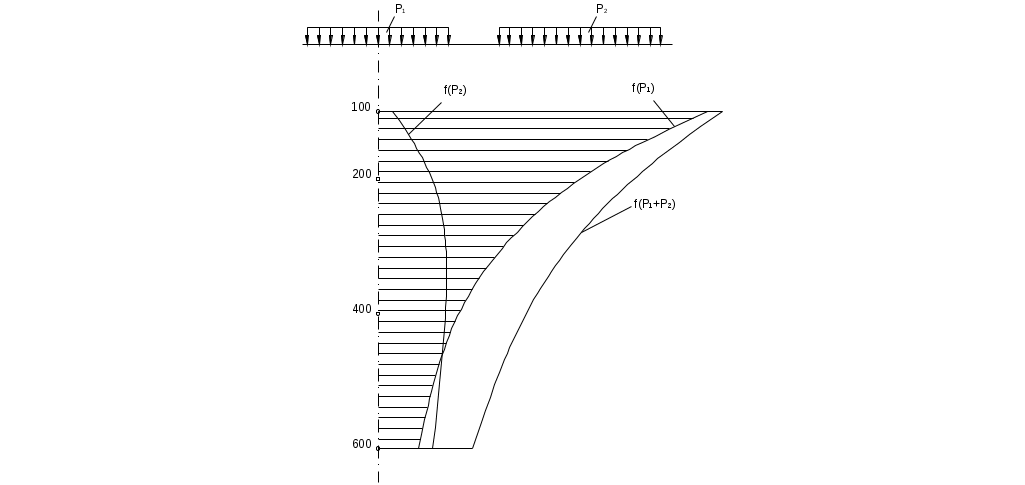
Рис. 3-2. Эпюры распределения вертикальных напряжений σZ
|
 Скачать 1.25 Mb.
Скачать 1.25 Mb.