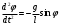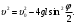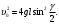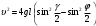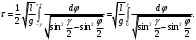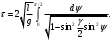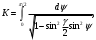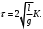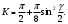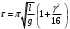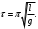Механика Работа 2 Математический маятник Введение
 Скачать 73.01 Kb. Скачать 73.01 Kb.
|
|
Механика Работа № 2 Математический маятник Введение
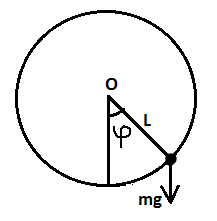
Чтобы практически реализовать устройство, близкое к идеальному круговому математическому маятнику, можно, например, закрепить компактный массивный груз на лёгком жёстком подвесе (стержне) длиной l, начало которого вращается на оси О. Угол φ определяется из дифференциального уравнения движения маятника
при начальных условиях 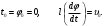 Силы трения стержня на оси и сопротивления движению со стороны среды (в нашем случае – воздуха) не учитываются. Используя закон сохранения энергии, можно получить выражение для угловой скорости  : :
При 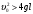 маятник совершает полные обороты. Для каждого значения маятник совершает полные обороты. Для каждого значения 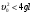 можно найти угол такой, что можно найти угол такой, что
В этом случае
и движение маятника представляет собой колебания по дуге 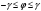 . . Период размаха (колебаний) определяется формулой
Подстановка 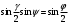 дает: дает:
Полученный интеграл называется полным эллиптическим интегралом первого рода и обозначается
так что
В математике доказано, что данный интеграл относится к разряду «неберущихся», его значение для каждого нужного γ можно найти численными методами с любой необходимой точностью. Значения К для некоторых γ приведены в таблице:
Приближенная формула для К при небольших значениях имеет вид:
При весьма малых полагают 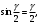 и тогда и тогда
Если угол столь мал, что членом 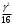 можно пренебречь, то можно пренебречь, то
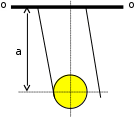
Получили формулу, хорошо знакомую из курса физики средней школы. Описание лабораторной установки
 сследуемый в лабораторной сследуемый в лабораторной установке маятник схематически изо- бражён на рис. 2. Он представляет со- бой шарик радиусом r на би- филярном подвесе: тонкая нить пропу- щена через центр шарика, концы нити закреплены на стойке. Такую систему можно применить вместо жёсткого подвеса, если γ ≤ π/2. Рис.2 Длина маятника (по вертикали от оси до центра шарика) может регулироваться в пределах нескольких сантиметров до примерно25 см. Время колебаний с точностью до миллисекунд измеряется электронным секундомером лабораторной установки и отображается на правом дисплее. На левом дисплее указывается количество завершившихся колебаний. Порядок выполнения работы Установить длину подвески, близкую к максимальной. Измерить длину получившегося математического маятника. Отрегулировать систему так, чтобы шарик в покое находился в створе оптического датчика. Включить кнопку «СЕТЬ». Отклонив маятник на 5 градусов вправо, плавно (без толчка) отпустить шарик, обеспечив тем самым начало процесса колебаний. Нажать и отпустить кнопку «СБРОС». Когда на счётчике количества колебаний появится цифра 9, нажать кнопку «СТОП». На правом дисплее вскоре появится цифра 10, а на левом – время, соответствующее десяти полным колебаниям. Повторить эксперимент ещё 4 раза. Результаты занести в таблицу, где должны быть указаны -длина маятника, угол первоначального отклонения, номер измерения, количество периодов и соответствующее им время колебаний, подсчитанное среднее время одного колебания (т.е. период колебаний), погрешность определения периода колебаний. Повторить пункт 3 для первоначального угла отклонения 10, а затем и 20 градусов. Результаты также занести в таблицу. Повторить пункты 3 и 4 для другой длины маятника. Объяснить результаты и сделать выводы. |