Экзамен. Межрегиональный центр переподготовки специалистов Экзамен По дисциплине Физика. Часть 2 Никитин Д. Н. Группа
 Скачать 141.13 Kb. Скачать 141.13 Kb.
|
|
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов Экзамен По дисциплине: Физика. Часть 2 Выполнил: Никитин Д.Н. Группа: ТБТ-92 Проверил: Моргачев Ю.В. Новосибирск, 2020 г. Билет №5 Превращения энергии при свободных незатухающих механических колебаниях. Функции кинетической и потенциальной энергий от времени. Колебательными процессами (колебаниями) называются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине, или колебания маятника являются свободными колебаниями. При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в ноль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по закону инерции. В тот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д. Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. Для груза на пружине : 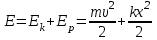 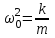 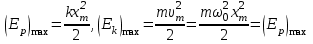 Для малых колебаний математического маятника: 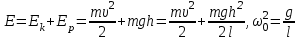 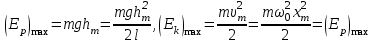 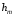 - максимальная высота подъема маятника в поле тяготения Земли; - максимальная высота подъема маятника в поле тяготения Земли; 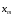 и и 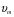 = = 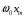 - максимальные значения отклонения маятника от положения равновесия и его скорости. - максимальные значения отклонения маятника от положения равновесия и его скорости.Р 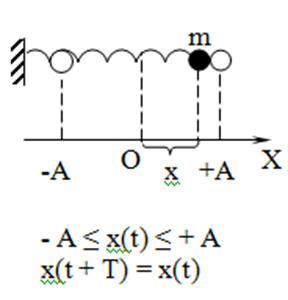 ассмотрим пружинный маятник. Когда мы выводим груз m из положения равновесия, мы сообщаем колебательной системе некоторую энергию, которая в системе будет сохраняться при отсутствии сил сопротивления, трения, т. е. полная энергия не изменяется с течением времени: Е = const. Между крайними точками отклонения, в крайних точках скорость грузика равна нулю ассмотрим пружинный маятник. Когда мы выводим груз m из положения равновесия, мы сообщаем колебательной системе некоторую энергию, которая в системе будет сохраняться при отсутствии сил сопротивления, трения, т. е. полная энергия не изменяется с течением времени: Е = const. Между крайними точками отклонения, в крайних точках скорость грузика равна нулюи положением равновесия, которое грузик проходит с максимальной скоростью, полная энергия Е равна сумме кинетической и потенциальной энергий: 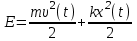 В крайних точках полная энергия: 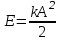 , а при прохождении положения равновесия: , а при прохождении положения равновесия: 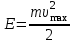 Таким образом, в пружинном маятнике происходит периодическое превращение кинетической энергии в потенциальную и обратно. Пусть 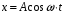 . Тогда кинетическая энергия равна . Тогда кинетическая энергия равна 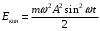 , а потенциальная , а потенциальная 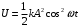 . Построим графики х(t), Екин(t) и U(t). . Построим графики х(t), Екин(t) и U(t).Из рисунка видно, что период Т1колебаний потенциальной и кинетической энергий в два раза меньше периода колебаний Т смещения х(t) грузика, т.е. 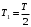 . Аналогично происходит периодическое превращение кинетической энергии в потенциальную и обратно при колебаниях физического и математического маятников. Конечно, при рассеянии (диссипации) энергии полная механическая энергия системы уменьшается со временем, что в конце концов приводит к прекращению колебаний. . Аналогично происходит периодическое превращение кинетической энергии в потенциальную и обратно при колебаниях физического и математического маятников. Конечно, при рассеянии (диссипации) энергии полная механическая энергия системы уменьшается со временем, что в конце концов приводит к прекращению колебаний.  Дифракция волн. Условие наблюдения дифракции. Виды дифракции. Принцип Гюйгенса-Френеля. Дифракция волн (лат. diffractus - буквально разломанный, переломанный) огибание препятствия волнами - явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы. Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах. Дифракция волн может проявляться: а) в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении; б) в разложении волн по их частотному спектру; в) в преобразовании поляризации волн; г) в изменении фазовой структуры волн. Виды дифракции Различают два вида дифракции: 1 MN - фронт волны. r0 - расстояние от Э до отверстия. В точке С волны будут интерферировать. Разбиваем площадь отверстия на зоны и проводим радиусы: Разбиваем площадь отверстия на зоны и проводим радиусы: . Дифракция на круглом отверстии (дифракция Френеля). 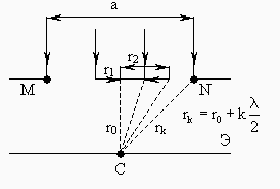 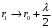 ; ; 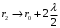 Крайние точки зон имеют разность хода 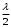 , поэтому точки в соседних зонах колеблются в противофазах и гасят друг друга. Итак: , поэтому точки в соседних зонах колеблются в противофазах и гасят друг друга. Итак:Если число зон, которое укладывается в отверстии чётное, то в точке С будет тёмное пятно, если нечётное, то светлое. Максимум освещения, когда размер отверстия a равен одной зоне. Число зон Френеля зависит от удалённости точки С (т.е. от r0) от фронта MN. Можно показать, если: 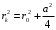 , где , где 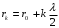 то то 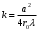 т.е. т.е. 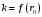 По мере удаления Э в точке С наблюдаются то тёмное, то светлое пятно. 2. Дифракция от щели (дифракция Фраунгофера). При прохождении лучей через узкую щель АС наблюдается дифракция. 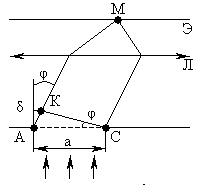 Пути лучей КМ и СМ таутахронны, т.е. равны. На их прохождение свет затрачивает одинаковое время. АС - щель.δ - разность хода лучей, от которого зависит результат интерференции: δ = аsinφ Если: 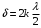 (чётное число зон) - min. (чётное число зон) - min.Условие min 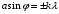 где k = 1,2,3…- порядок дифракционного минимума. где k = 1,2,3…- порядок дифракционного минимума. аналогично: 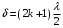 нечетное число - max. нечетное число - max.Условие max 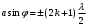 при при 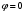 - центральный max. - центральный max.Принцип Гюйгенса - Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса - Френеля и дифракционные явления. Принцип Гюйгенса — Френеля формулируется следующим образом: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. Колебательный контур состоит из катушки индуктивностью 0,2 мГн и плоского конденсатора с площадью пластин 155 см2 и расстоянием между ними 1,5 мм. Контур резонирует на длину волны 630 м. Вычислите диэлектрическую проницаемость среды между пластинами конденсатора. Решение: Емкость плоского конденсатора определяется по формуле: 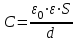 Период колебаний определим: 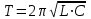 Зависимость длины волны от периода колебаний: 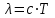 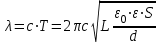 , тогда , тогда 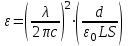 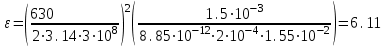 Ответ: диэлектрическая проницаемость среды 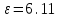 Ф/м Ф/м |
