Методы обработки результатов измерений. Методы обработки. Методы обработки результатов измерений Цель работы
 Скачать 39.93 Kb. Скачать 39.93 Kb.
|
|
Методы обработки результатов измерений Цель работы Ознакомиться с методикой обработки и представлением результатов прямых многократных равноточных измерений с учетом требований ГОСТ 8.736 - 2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. Получение навыков практического пользования таблицами ГОСТ 8.736-2011 ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. Краткие теоретические сведенияПорядок обработки результатов равноточных измерений ЧАСТЬ 1При многократном взвешивании массы получены значения: 94,7; 98,3; 101,2; 96,7 (кг). Систематическая погрешность весов составляет +0,6 кг. Укажите доверительные границы истинного значения массы с вероятностью Р = 0,95 Исключаем известные систематические погрешности (сист) из результатов измерений (систематическая погрешность средства измерения принимается равной его абсолютной погрешности (си), взятой с противоположным знаком). Погрешность (Δ си) по условию задачи равна +0,6 кг, тогда: 94,7 - 0,6 = 94,1 98,3 - 0,6 = 97,7 101,2 - 0,6 = 100,6 96,7 - 0,6 = 96,1 Проверяем результаты наблюдений на наличие грубых выбросов (промахов) по критерию Романовского: 94,1<96,1<97,7<100,6 б) определяем размах результатов измерений: R = xmax – xmin; R = 101,8 – 95,3 = 6,5 в) определяем среднее арифметическое значение результатов измерений:
n = 4 M[x] ≈ = 393,3/4 = 98,3 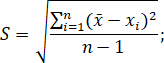 г) определяем среднюю квадратическую погрешность результатов единичных измерений г) определяем среднюю квадратическую погрешность результатов единичных измерений℺ = S(х) = 2,745 д) находим соотношение для проверяемого результата, применяя критерий Романовского: βt выбираем по таблице В1 (прил. В) для заданной доверительной вероятности Р = 0.95 (уровень значимости 5). Подставляя в данную формулу результаты измерений, получим следующие значения. Результат в числителе рассчитываем по модулю:
Сравнивая полученные результаты с таблицей В1 (уровень значимости 5 и n =4, βt = 1,710), можем сделать вывод, что наивысший результат u = 1,28 является нормальным, а значит остальные результаты допускаются. Таблица 1
Sх̅ = 1,3726 Вычисляем доверительные границы погрешности результата измерений по заданным значениям доверительной вероятности Р = 0,95: где tpnкоэффициент Стьюдента (Таблица Б1) при n=4, Р= 0,95, tpn= 3,18 Запишем результаты измерений (для Р = 0.95) с использованием правил округления: 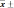 а) x = x, Р =0,95; т.е. а) x = x, Р =0,95; т.е.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Число измерений, n | Вероятность Р | ||
| 0.9 | 0.95 | 0.99 | |
| tpn | - | 3,18 | - |
| xmin | - | 93,93 | - |
| xmax | - | 102,67 | - |
Вывод!
Я ознакомился с методикой обработки и представлением результатов прямых многогранных равноточных измерений с учетом требований ГОСТ 8.736 – 2011 Государственная система обеспечения единства измерений. Получил навыки практического пользования таблицами ГОСТ 8.736-2011 ГСИ.
