курсовая. Методы обучения начльному курсу математики. Методы обучения начальному курсу математики
 Скачать 66.07 Kb. Скачать 66.07 Kb.
|
|
Тема: Методы обучения начальному курсу математики. Цель занятия: Основные дидактические принципы обучения математике. Методы обучения математике в начальной школе и их классификация. Проблемный метод обучения математике. Метод моделирования в обучении начальному курсу математики. Направленность методов обучения математике на развитие умственного и познавательного потенциала младшего школьника. Средства занятия: Лекционный материал. Интерактивная доска (презентация методов обучения в виде таблиц и основных определений и выводов). Презентация. Планируемые результаты занятия: Учащиеся должны уметь: - методы обучения математике в системе начальной школы; - приоритетные методы обучения в современной школе; - зависимость выбора метода обучения от общих целей и задач обучения, а также от темы и содержания изучаемого материала. Знать основные идеи и методику использования проблемного метода обучения математике. Метод математического моделирования – как наиболее плодотворный, доступный и мощный в процессе познания окружающего мира, а также прогнозирования результатов своей деятельности. ОСНОВНЫЕ ДИДАКТИЧЕСКИЕ ПРИНЦИПЫ В ОБУЧЕНИИ МАТЕМАТИКЕ Дидактика (от греч. didaktikos – поучающий) – отрасль педагогики, разрабатывающая теорию образования и обучения. Предметом дидактики являются закономерности и принципы обучения, его цели, научные основы содержания образования, методы, формы и средства обучения. Задачами дидактики являются: описание и объяснение процесса обучения и условий его реализации; разработка более совершенной организации процесса обучения, новых обучающих систем и технологий. В дидактике обобщены те положения в обучении учебной дисциплине, которые имеют универсальный характер. Принципы обучения – это руководящие идеи, нормативные требования к организации и проведению дидактического процесса. Они носят характер общих указаний, правил, норм, регулирующих процесс обучения. Принципы обучения – это система важнейших требований, соблюдение которых обеспечивает эффективное и качественное развитие учебного процесса. Дидактические принципы обучения математике представляют, по существу, совокупность единых требований, которым должно удовлетворять обучение математике, и включают принципы: научности; воспитания; наглядности; доступности; сознательности и активности; прочности усвоения знаний; систематичности; последовательности; учета возрастных особенностей; индивидуализации обучения; воспитывающего обучения. В основу концепции математического образования положены принципы: научности; сознательности, активности и самостоятельности; доступности; наглядности; всеобщности и непрерывности математического образования на всех ступенях средней школы; преемственности и перспективности содержания образования, организационных форм и Методов обучения; систематичности и последовательности; системности математических знаний; дифференциации и индивидуализации математического образования, создания таких условий, при которых возможен свободный выбор уровня изучения математики; гуманизации; усиления воспитательной функции; практической направленности обучения математике; компьютеризации обучения и т.д. ЗАКОНЫ ПЕДАГОГИЧЕСКИХ НОВШЕСТВ Понять динамику развития и противоречий инновационных процессов в системе образования помогают законы педагогических новшеств. Закон необратимой дестабилизации педагогической инновационной среды. Любой инновационный процесс в системе образования при его реализации с неизбежностью вносит необратимые изменения в инновационную социально-педагогическую среду, в которой он осуществляется. В результате этого целостные представления о каких-либо педагогических процессах или явлениях начинают разрушаться. Такое вторжение педагогического новшества в социально-педагогическую среду приводит к поляризации мнений о нем, о его значимости и ценности. Чем значительнее педагогическое новшество, тем основательнее дестабилизация, которая касается инновационной среды разного типа: теоретической, опытной, коммуникативной и практической. Закон финальной реализации инновационного процесса. Любой инновационный процесс рано или поздно, стихийно или сознательно реализовывается и заканчивает свое существование как новшество. Показателен в этом отношении опыт В.А. Шаталова. Закон стереотипизации педагогических инноваций. Любая педагогическая инновация имеет тенденцию превращаться в стереотип мышления и практического действия. В этом смысле она обречена на рутинизацию, она становится стереотипом, барьером на пути реализации других новшеств. Закон цикловой повторяемости педагогического новшества. Характерной особенностью системы образования является повторное возрождение какого-либо явления или новшества в новых условиях. Именно поэтому в педагогической теории и практике новшества вызывают особое противодействие, так как воспринимаются частью учителей как «давно забытое старое». В качестве примеров можно привести конспекты ВА Шагалова, в которых многие не видят нового из-за того, что они давно используются в педагогике, а также коммунарскую методику, восстановленную в новых условиях в ряде школ (например, школа В.А. Караковского). Этими законами не ограничиваются общие и специфические для педагогической инноватики закономерности, которые еще предстоит исследовать. МЕТОДЫ ОБУЧЕНИЯ МАТЕМАТИКЕ И ИХ КЛАССИФИКАЦИЯ Традиционное обучение имеет ряд недостатков. Из них следует выделить: – преобладание словесных методов изложения, способствующих рассеиванию внимания и невозможности его акцентирования на сущности учебного материала; – средний темп изучения математического материала; – большой объем материала требующего запоминаний; – недостаток дифференцированных заданий по математике и др. Недостатки традиционного обучения математике можно устранить путем усовершенствования процесса ее преподавания. Метод (от греч. methodos – путь исследования) – способ достижения цели. Метод обучения – упорядоченный комплекс дидактических приемов и средств, с помощью которых реализуются цели обучения и воспитания. Метода обучения включают взаимосвязанные, последовательно чередующиеся способы целенаправленной деятельности учителя и учащихся. Любой метод обучения предполагает цель, систему действий, средства обучения и намеченный результат. Объектам и субъектом метода обучения является ученик. Какой-либо один метод обучения используется в чистом виде лишь в специально спланированных учебных или исследовательских целях. Обычно преподаватель сочетает различные методы обучения. Метод обучения – историческая категория. На протяжении всей истории педагогики проблема методов обучения разрешалась с различных точек зрения: через формы деятельности; через логические структуры и функции форм деятельности; через характер познавательной деятельности. Сегодня существуют разные подходы к современной теории методов обучения. Классификация методов обучения проводится по различным основаниям. По характеру познавательной деятельности: – объяснительно-иллюстративные (рассказ, лекция, беседа, демонстрация и т.д.); – репродуктивные (решение задач, повторение опытов и т.д.); – проблемные (проблемные задачи, познавательные задачи и т.д.); – частично-поисковые — эвристические; – исследовательские. По компонентам деятельности: – организационно-действенные – метода организации и осуществления учебно-познавательной деятельности; – стимулирующие – метода стимулирования и мотивации учебно-познавательной деятельности; – контрольно-оценочные – метода контроля и самоконтроля эффективности учебно-познавательной деятельности. По дидактическим целям: – методы изучения новых знаний; – методы закрепления знаний; – методы контроля. По способам изложения учебного материала: – монологические — информационно-сообщающие (рассказ, лекция, объяснение); – диалогические (проблемное изложение, беседа, диспут). По формам организации учебной деятельности. По уровням самостоятельной активности учащихся. По источникам передачи знаний: – словесные (рассказ, лекция, беседа, инструктаж, дискуссия); – наглядные (демонстрация, иллюстрация, схема, показ материала, график); – практические (упражнение, лабораторная работа, практикум). По учету структуры личности: – сознание (рассказ, беседа, инструктаж, иллюстрирование и др.); – поведение (упражнение, тренировка и т.д.); – чувства – стимулирование (одобрение, похвала, порицание, контроль и т.д.). Все указанные классификации рассматриваются в дидактическом аспекте. Педагогическая классификация разделяет методы преподавания и методы изучения (учения). Последние, в свою очередь, представлены научными (наблюдение, анализ, синтез и т.д.) и учебными (эвристический, обучение на моделях и др.) методами изучения математики. Методы, преподавания – средства й приемы, способы информации, управления и контроля познавательной деятельности учащихся. Методы учения – средства и приемы, способы усвоения учебного материала, репродуктивные и продуктивные приемы учения и самоконтроля. Основными методами математического исследования являются: наблюдение и опыт; сравнение; анализ и синтез; обобщение и специализация; абстрагирование и конкретизация. Современные методы обучения математике: проблемный (перспективный), лабораторный, программированного обучения, эвристический, построения математических моделей, аксиоматический и др. Рассмотрим классификацию методов обучения (схема 1). 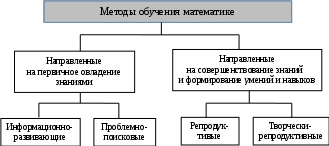 Схема 1. Классификация методов обучения Информационно-развивающие методыделятся на два класса: Передача информации в готовом виде (лекция, объяснение, демонстрация учебных кинофильмов и видеофильмов, слушание магнитозаписей и др.); Самостоятельное добывание Зданий (самостоятельная работа с книгой, с обучающей программой, с информационными базами данных – использование информационных технологий). Проблемно-поисковые методы: проблемное изложение учебного материала (эвристическая беседа), учебная дискуссия, лабораторная по- исковая работа (предшествующая изучению материала), организация коллективной мыслительной деятельности в работе малыми группами, организационно-деятельностная игра, исследовательская работа. Репродуктивные методы: пересказ учебного материала, выполнение упражнения по образцу, лабораторная работа по инструкции, упражнения на тренажерах. Творчески-репродуктивные методы: сочинение, вариативные упражнения, анализ производственных ситуаций, деловые игры и другие виды имитации профессиональной деятельности. Составной частью методов обучения являются приемы учебной деятельности учителя и учащихся. Методические приемы – действия, способы работы, направленные на решение конкретной задачи. За приемами учебной работы скрыты приемы умственной деятельности (анализ и синтез, сравнение и обобщение, доказательство, абстрагирование, конкретизация, выявление существенного, формулирование выводов, понятий, приемы воображения и запоминания). Современные методы обучения, главным образом, ориентированы на обучение не готовым знаниям, а деятельности по самостоятельному приобретению новых знаний, т.е. познавательной деятельности. Специальные методы — это адаптированные для обучения основные методы познания, применяемые самой математике, характерные для математики методы изучения действительности (построение математических моделей, способы абстрагирования, используемые при построении таких моделей, аксиоматический метод). ПРОБЛЕМНОЕ ОБУЧЕНИЕ Проблемное обучение – это дидактическая система, основанная на закономерностях творческого усвоения знаний и способов деятельности, включающая сочетание приемов и методов преподавания и учения, которым присущи основные черты научного поиска. Проблемный метод обучения – обучение, протекающее в виде снятия (разрешения) последовательно создаваемых в учебных целях проблемных ситуаций. Проблемная ситуация – осознанное Затруднение, порождаемое несоответствием между имеющимися знаниями и теми знаниями, которые необходимы для решения предложенной задачи. Задача, создающая проблемную ситуацию, называется проблемой, или проблемной задачей. Признаками проблемы являются: – порождение проблемной ситуации; – определенные готовность и интерес решающего к поиску решения; – возможность неоднозначного пути решения, обусловливающая наличие различных направлений поиска. Проблема должна быть доступной пониманию учащихся, а ее формулировка – вызывать интерес и желание учащихся ее разрешить. Следует различать проблемную задачу и проблему. Проблема шире, она распадается на последовательную или разветвленную совокупность проблемных задач. Проблемную задачу можно рассматривать как простейший, частный случай проблемы, состоящей из одной задачи. Например, можно поставить проблему изучения ромба. Одна из проблемных задач, входящих в эту учебную задачу, состоит в открытии свойства диагоналей ромба. Проблемное обучение ориентировано на формирование и развитие способности учащихся к творческой деятельности и потребности в ней. Проблемное обучение целесообразно начинать с проблемных задач, подготавливая тем самым почву для постановки учебных задач. Существуют три основных типа учебных проблем: Проблема математизации, математического описания, перевода на язык математики ситуаций и задач, возникающих вне или внутри математики, т.е. проблема построения математических моделей. Проблема исследования различных классов моделей, результатом решения проблем этого типа является дальнейшее развитие системы теоретических знаний путем включения в нее новых «маленьких теорий». Проблема применения новых теоретических знаний в новых ситуациях, перенос математических знаний на изучение новых объектов. Рассмотрим деятельность учителя и учащихся в условиях Применения проблемного метода в обучении математике (табл. 1). Таблица 1.
Проблемное обучение имеет структуру: Актуализация изученного материала. Создание проблемной ситуации. Постановка учебной проблемы. Построение проблемной задачи. Поиск и решение проблемы (формулирование гипотезы, доказательство гипотезы, анализ подходов, обобщение). Проверка решения проблемы. Исследование. Анализ результатов поиска. При проблемном обучении учитель не сообщает учащимся готовых знаний, а организует учащихся на их поиск. Математические понятия, закономерности, теории излагаются в ходе поиска, наблюдения и анализа. Проблемное обучение реализуется успешно лишь при определенном стиле общения между учителем и учащимися, когда возможна свобода выражения своих мыслей, когда диалог между учителей и учащимися происходит в доброжелательной обстановке. Проблемность является неотъемлемой чертой педагогического процесса, однако не всякое занятие можно назвать проблемным. Все зависит от того, какой объем методов и организационных форм, свойственных проблемному обучению, используется на занятии. Проблемное обучение имеет свои преимущества и недостатки. В качестве преимуществ можно отметить: развитие мыслительной деятельности учащихся, математических способностей; формирование интереса к учению; воспитание активности в обучении, творческого начала. Существенным недостатком такого обучения является необходимость больших временных затрат, а также специальной методической подготовки учителя. ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ Программированное обучение – это такое обучение, когда решение задачи представлено в виде строгой последовательности элементарных операций, в обучающих программах изучаемый материал подается в форме строгой последовательности кадров, каждый из которых содержит, как правило, дозу нового материала и контрольный вопрос или задание. Программированное обучение предусматривает: – правильный отбор и разбивку учебного материала на небольшие дозы; – частый контроль знаний; – переход к следующей дозе учебного материала лишь после ознакомления учащегося с правильным ответом или характером допущенной им ошибки; – обеспечение возможности каждому ученику работать со свойственной ему, индивидуальной скоростью усвоения. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Одним из наиболее плодотворных методов математического познания действительности является метод построения математических моделей изучаемых реальных объектов или объектов, уже описанных в других областях знаний с целью их глубокого изучения и решения всех возникающих в этих реальных ситуациях задач с помощью математического аппарата. Математическая модель — это приближенное описание какого-либо класса явлений, выраженное на языке математической теории (с помощью алгебраических функций или их систем, дифференциальных или интегральных уравнений или неравенств, системы геометрических предложений или других математических объектов). Метод математического моделирования состоит из четырех этапов: Поиск языка и средств для перевода задачи в математическую, т.е. построение математической модели. Изучение математической модели, ее исследование, расширение теоретических знаний учащихся. Поиск решения математической задачи, рассмотрение различных способов решения, выбор наиболее рационального пути решения. Перевод результата решения математической задачи в исходный, анализ модели в связи с накоплением данных об изучаемых явлениях н модернизация модели, а в будущем — построение новой, более совершенной математической модели. Анализ математической модели позволяет проникнуть в сущность изучаемых явлений. Математическая модель — мощный метод познания внешнего мира, а также прогнозирования и управления. Метод математического моделирования, сводящий исследование явлений внешнего мира к математическим задачам, занимает ведущее место среди других методов исследования. Методом математического моделирования решаются многие задачи межпредметного характера. С помощью метода математического моделирования раскрывается двойная связь математики с реальным миром. С одной стороны, математика служит практике по изучению и освоению объектов окружающего нас реального мира, с другой - сама жизнь, практика способствует дальнейшему развитию математики и направляет это развитие. Разберем и проведем решение и анализ простой задачи, используя метод математического моделирования. Задача. На площадке играли 3 ребят, к ним присоединились еще 2 ребят. Сколько детей всего играют на площадке? Моделируем условие и решение задачи. I способ. Играло – 3 ребят Подошло – 2 ребят Стало – ? 3 + 2 = 5 (реб.) II способ.
3 + 2 = 5 (реб.) III способ.           + = + = ? 3 + 2 = 5 (реб.) IV способ.  0 1 2 3 4 5 ? 3 + 2 = 5 (реб.) V способ.   A B A B     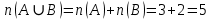 (реб.) (реб.)Вывод: Моделирование любых математических объектов языком математической символики с применением математической терминологии приводит: – к возможности более понятного восприятия изучаемого материала младшим школьником; – расширяет кругозор ребенка; – углубляет его математические познания; – прививает интерес к предмету; – повышает мотивацию к обучению; – повышает самооценку ученика (Я – могу, Я – понимаю, Я – сумею и т.д.). |
