Структурный анализ. структ анализ. Методы описания структур
 Скачать 392 Kb.
|
|
Анализ связей. Исследование особенностей связей между элементами структуры направлены прежде всего на выявление в соответствующем графе петель, контуров и сильносвязных подграфов. Петля интерпретируется как наличие связи между входом и выходом одного и того же элемента. Контур образует путь – чередующуюся последовательность ребер и вершин, в котором начальная и конечная вершины совпадают. Пример. В рассматриваемом на рис.5 графе имеется одна петля и два пути (4-6, 9; 6.9-11). Путь 1    9 10 11 п       уть 2 петля 4 5 6 7 8             1 2 3Рис.5. Петля и пути в графе Подграф называется сильсвязным, если все входящие в него вершины взаимно достижимы, т.е. из любой вершины подграфа можно попасть в любую другую вершину. Пусть Qi –множество вершин графа, достижимых из вершины I, а  - множество вершин графа, из которых можно достичь i. Из определения сильносвязного подграфа следует, что пересечение  содержит вершины, принадлежащие одному сильсвязному подграфу. Поэтому нахождение Q(i) равносильно определению сильносвязного подграфа, включающего в себя вершину i. Последовательно перебирая i и определяя множества Q(i) до тех пор, пока в эти множества не войдут все вершины графа, можно найти его разбиение на сильносвязные подграфы.Для графа на рис.4 найдем множества Q(1)={1,4,5,6,9,10,11}  {1}={1}Q(2)={2,4,5,6,7,9,10,11} {2}={2}Q(3)={3,4,5,6,7,8,9,10,11} {3}={3}Q(4)={4,5,6,7,9,10,11} {1,2,3,4,5,6,7,8,9,10,11}={4,5,6,9,10,11}Q(6)=Q(5)=Q(4) Q(7)={4,5,6,7,9,10,11} {2,3,7,8}={7}Q(8)={4,5,6,7,8,9,10,11} {8}={8}Множества Q(i),I=1,2,…8 содержат все вершины графа. Теперь исходный граф можно разбить на сильносвязные подграфы G(1), G(2), G(3), G(4), G(7), G(8), G(12), из которых только G(4) является нетривиальным (содержит больше одной вершины). Представим найденные сильносвязные подграфы как вершины нового графа (рис.6). Если между вершинами сильносвязных подграфов G(i) и G(k) в исходном графе имеется хотя бы одно ребро, то в конденсированном графе G(i) и G(k) также соединяются соответственно направленным ребром. Конденсированный граф проще исходного, к тому же в нем отсутствуют контуры и петли. G(4) G(7) G(8) G(12)     G(1) G(2) G(3) Рис.6 Конденсация исходного графа Построение конденсаций можно рекомендовать для сложных структур, содержащих большое число элементов. Непосредственное исследование таких структур затруднено, а выделение конденсаций позволяет сосредоточить внимание на анализе существенных связей, в наибольшей степени характеризующих особенности взаимодействия элементов системы. Связность. В теории графов под связностью графа понимается наименьшее число вершин, удаление которых из графа приводит к несвязному (содержащему изолированные вершины) или тривиальному (состоящему из одной вершины) графу. Вводится также понятие реберной связности – наименьшего числа ребер, удаление которых приводит к несвязному или тривиальному графу. Обе эти характеристики достаточно сложно вычислить Еще сложнее дать в процессе анализа структуры конкретной системы подходящую физическую интерпретацию. Поэтому для оценки связности структур чаще используется показатель  , характеризующий относительную разность связей R, имеющихся в данной структуре и числа связей Rmin, минимально необходимого для связанности графа структуры. Показатель  интерпретируется обычно как мера избыточности структуры графа по связям.Если граф содержит n вершин, то Rmin=т-1 независимо от того, является граф ориентированным или нет. Следовательно, 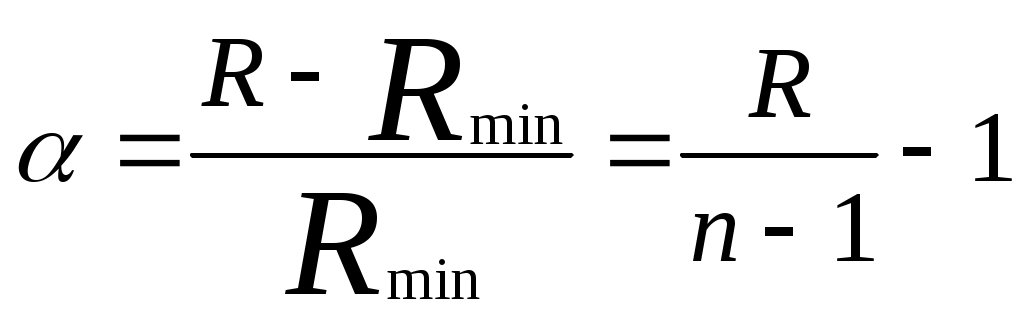 Значение R определяется по матрице смежности для ориентированных и неориентированных графов по-разному. В ориентированном графе каждому ребру (i,j) соответствует единичный элемент матрицы смежности  ; в неориентированном графе таких элементов будет два:  . Поэтому для ориентированного и неориентированного графов соответственно имеем: ; Пример. Дан граф, представленный на рис.7. 7 8     4 5 6        1 2 3Рис. 7. Граф, избыточный по связям Граф описывается матрицей смежности 1 2 3 4 5 6 7 8 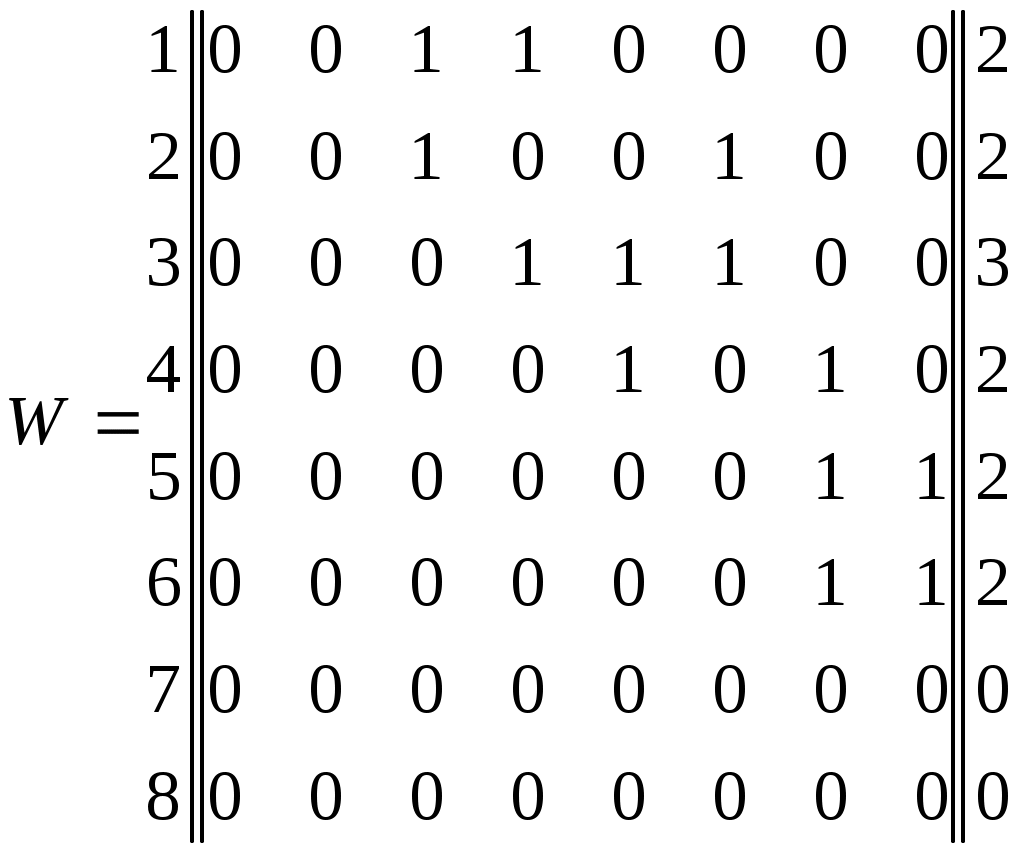 (5)на основе которой рассчитываются значения  (i=1,2,…,9), которые представлены столбцом чисел справа от матрицы V. Величина составляет  , свидетельствующей о наличии избыточности по связям.Диаметр структуры. Пусть  - длина минимального пути между висячей вершиной i и тупиковой вершиной j, равная числу ребер, составляющих этот путь. Тогда, если I и J –множества висячих и тупиковых вершин графа соответственно, то диаметр структуры   ,характеризует максимальное число связей, разделяющих входные и выходные элементы структуры. По значению можно косвенно судить о ряде предельных параметров системы, в частности о ее надежности, длительности задержек сообщений, идущих от висячих вершин к тупиковым, инерционности.Определение значений  сводится к задаче поиска кратчайшего пути на графе для каждой пары (i,j) такой, что  , . Эта задача может быть решена методом динамического программирования.Для графа, приведенного на рис.7 имеем (в предположении, что стоимость каждого шага равна единице)  Степень централизации. Для характеристики неравномерности загрузки элементов структуры, описываемой неориентированным графом, предложен индекс центральности 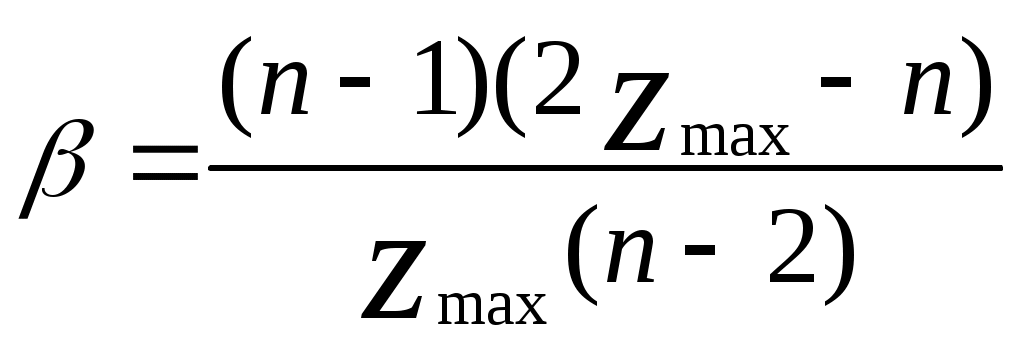 где 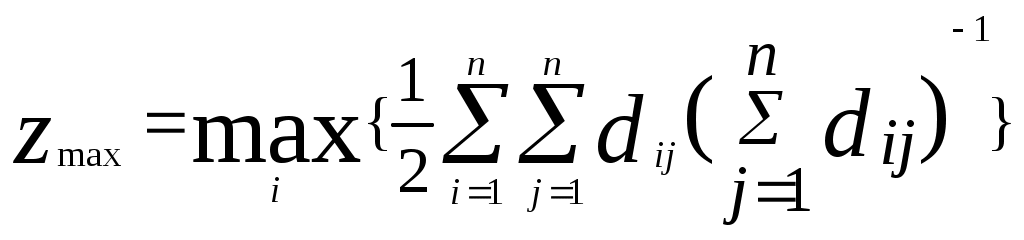 ,причем для всех i=j естественным образом полагается  .Пример. Граф рассредоточенной структуры (рис.8) соответствует             Рис.8 Граф рассредоточенной структуры Графу централизованной структуры (рис.9) соответствует       Рис.9 Граф централизованной структуры Индекс центральности для ориентированного графа, обладающего теми же свойствами, что и  , можно представить в виде где V(i)=  - суммарное число входящих и исходящих ребер из i-й вершины, а . Пример. Для графа, представленного на рис. 7, воспользовавшись матрицей смежности (5), получаем V(1)=V(2)=V(8)=2; V(3)=5; V(4)=V(5)=V(6)=4; V(7)=3 и, следовательно, V(k)=V(3)=5, а   Это соответствует структуре, у которой связи распределены неравномерно, но ясно выраженные центральные элементы отсутствуют. Сложность. Понятие сложности с трудом поддается формализации и имеет обычно субъективный оттенок. Если функциональные системы представить себе как процесс переработки входных воздействий в выходные, направленный соответственно от входных элементов системы к выходным, то можно предположить, что изучать свойства этого процесса будет тем труднее, чем разнообразнее пути, ведущие от входа к выходу системы. В основе одного из подходов к оцениванию сложности структуры лежит использование выражения 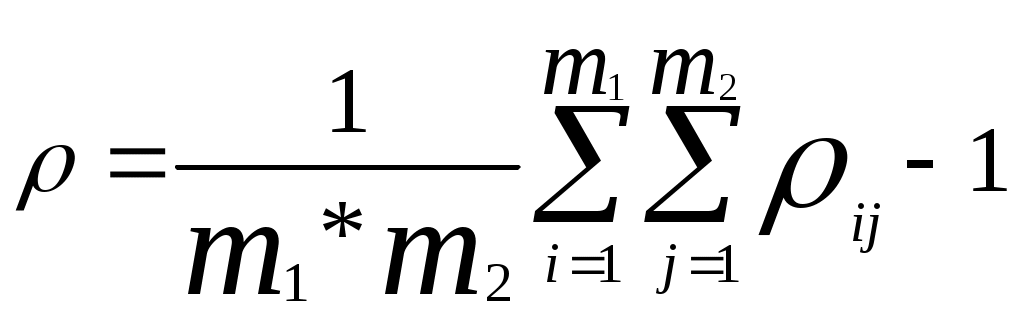 , (6)в котором  и  - число висячих и тупиковых вершин в графе структуры, а |