Структурный анализ. структ анализ. Методы описания структур
 Скачать 392 Kb.
|
 Моделирование структур Методы описания структур Топологический анализ структур Методы описания структур При анализе структур интересуются свойствами и характеристиками системы, не зависящими от времени, и сохраняющимися постоянными, неизменными на всем промежутке функционирования системы или достаточно длительной его части. С  труктурные и функциональные свойства системы тесно связаны между собой. Изучив законы функционирования отдельных элементов системы, но не зная структуры, нельзя представить систему как целое и, следовательно, понять, как она функционирует. Таким образом, анализ функционирования и изучение структуры являются двумя взаимосвязанными, дополняющими друг друга стадиями исследования любой системы.П  од структурой понимается совокупность тех свойств системы, которые являются существенными с точки зрения проводимого исследования и обладают инвариантностью на всем интересующем исследователя интервале функционирования или на каждом непересекающемся подмножестве, на которые разбит интервал функционирования.Структура может включать в себя как общесистемные свойства (наличие элементов, существование связей между ними и т.п.), так и специальные, присущие только данной конкретной системе и связанные с особенностями её функционирования (специфика отношений между элементами, закономерности распределения информационных, материальных и иных потоков и т.п.). В зависимости от целей изучения исследователя будут интересовать различные инвариантные во времени свойства системы. Из этого следует, что для одной и той же системы можно построить различные структуры и между системой и её структурой отсутствует однозначное соответствие. Формирование структуры является частью решения общей задачи построения системы, причем такой, которая не определяет заранее систему в целом, а лишь выявляет её конфигурацию. Построение структуры – самостоятельная задача, предваряющая синтез системы в целом, и облегчающая его проведение. Рассмотрим основные методы формализованного описания структурных свойств системы. Структурная схема. Если изобразить систему как совокупность блоков, осуществляющих некоторые функциональные преобразования, и связей между ними, то получим структурную схему, в обобщенном виде описывающую структуру системы. Под блоком обычно понимают, особенно в технических системах, функционально законченное отдельное устройство. Но, вообще говоря, членение на блоки может не соответствовать этому принципу и может осуществляться исходя из требуемой степени детализации описания структуры, наглядности отображения в ней особенностей процессов функционирования, присущих системе. Помимо функциональных в структурную схему могут включаться логические блоки, позволяющие изменять характер функционирования в зависимости от того, выполняются или нет некоторые заданные условия. Пример. Структурная схема двухуровневой системы управления представлена на рис.1. К0             К1 К2 К3          X Y Р   Рис.1 Структурная схема двухуровневой системы управления P-управляемый процесс со входом X и выходом Y;  -управляющие блоки нижнего уровня; -управляющие воздействия, вырабатываемые управляющими блоками соответственно на основании характеристик состояния  процесса Р; -блок управления верхнего уровня; -воздействия, координирующие работу блоков на основании поступающей от них информации  о процессе Р и своих действиях.Алгоритм работы координирующего устройства также представляет собой некоторую систему вычислительных операций. Структурная схема алгоритма для пары (  , i= 1,2,3 ) имеет вид (рис.2)В отличие от предыдущей данная структурная схема содержит логический блок, позволяющей системе действовать различным образом в ситуации, когда  отклонилось от нормы или, напротив, находится в заданных пределах.Структурные схемы наглядны и вмещают в себя информацию о большом числе структурных свойств системы. Кроме того, структурные схемы легко поддаются уточнениям и конкретизации, в ходе которой не надо изменять всю схему, а достаточно заменить отдельные её элементы структурными схемами, включающими не один, как раньше, а несколько взаимодействующих блоков. Однако структурная схема – это ещё не математическая модель структуры. Она с трудом поддается формализации и является скорее мостом, облегчающем переход от содержательного описания системы к математическому, чем действенным инструментом анализа и формирования структуры. Графы. Отношения между элементами структуры могут быть представлены соответствующим графом. Графом называется пара G=(A,B), в котором А - множество вершин,  В:А В – множество ребер (дуг).             нет да Рис.2. Структурная схема алгоритма работы координирующего устройства. Для того, чтобы облегчить анализ, вершины графа обычно нумеруются. Граф с пронумерованными вершинами называется отмеченным. Каждое ребро графа связывает две вершины, называемые в этом случае смежными. Если все ребра графа заданы упорядоченными парами (i,j) , в которых порядок расположения номеров смежных вершин имеет значение, то граф называется ориентированным. Неориентированный граф не содержит ориентированных ребер; в частично ориентированном графе ориентированы не все ребра. На рис. 3 приведены графы, соответствующие структурным схемам, представленным на рис.1 и рис.2. а) б)  1  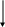 К 0   2 К1 К2 К3  3 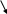 Р4 Рис.3. Неориентированный (а) и ориентированный (б) графы структурных схем Методика построения графа по структурной схеме проста: с вершинами графа сопоставляют блоки, а с ребрами – связи между блоками. Однако получающееся при этом изображение недостаточно для проведения формального анализа структур. Поэтому разработаны помимо геометрических и другие способы задания графов, позволяющие выполнить формальный анализ структур. Ориентированный граф можно задать матрицей смежности вершин V=  , в котором  =1, если граф содержит ребро (i,j), и =0 в противном случае. Аналогично строятся матрицы смежности и для неориентированных графов.Используются и другие формы записи матричных графов. Например, матрицей инциденций W=  , в которых 1, если i-начальная вершина ребра j;  = -1, если i-конечная вершина ребра j;0, в остальных случаях. Для графа б), представленного на рис.3, имеем матрицы: 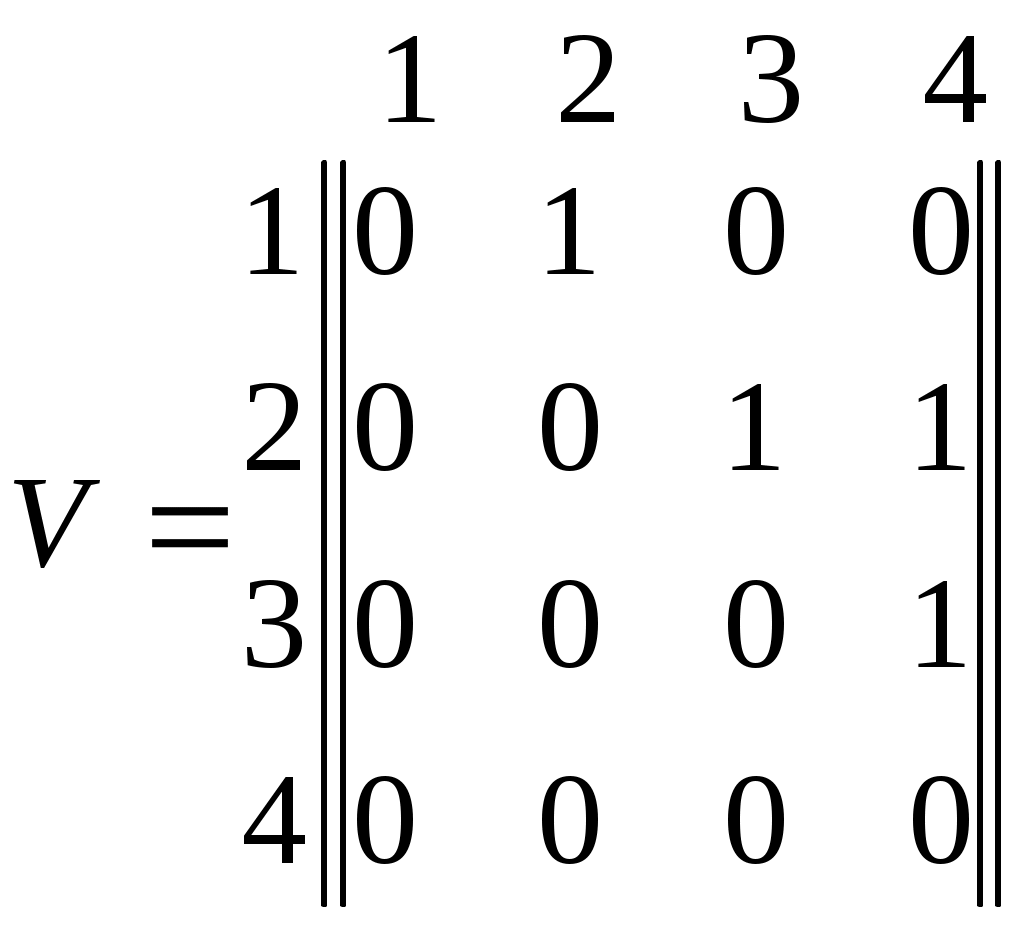 (1) 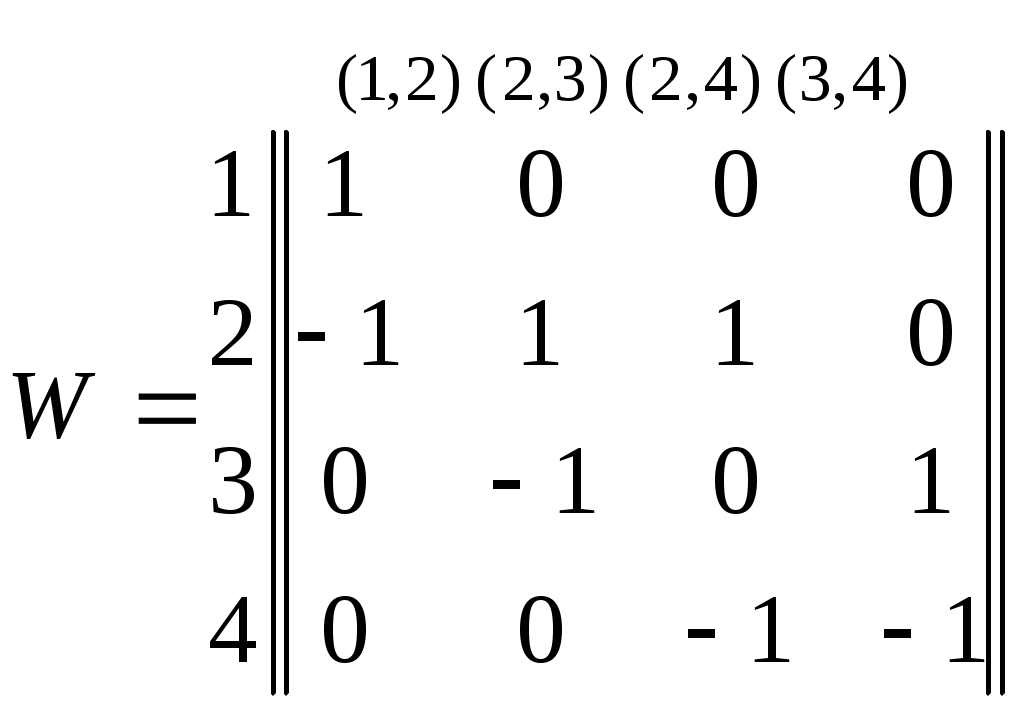 Если граф неориентирован, матрица инциденций содержит только 0 и 1; =1, если имеется ребро (i,j), и  в противоположном случае.Большое число нулей в матрицах (1) свидетельствует о неэкономичности этих форм представления графов, что особенно существенно, если графы содержат большое число вершин. Поэтому помимо матриц смежности и инциденций используются списковые формы записи графов. Список представляет собой множество R={R(i)}. Каждый элемент R(i)  R есть множество вершин графа, в которые можно непосредственно попасть из i-й вершины. Следовательно, в элемент R(i) включаются те вершины j, для которых в графе имеется ребро (i,j). Список, задающий граф, показанный на рис.3, имеет видR={R(1)={2}, R(2)={3,4}, R(3)={3}, R(4)=0} (2) Эту же запись можно представить более лаконично: R={1(2), 2(3,4), 3(3), 4(0)}, (3) если элементы множеств R(i) записать в круглых скобках, перед которыми проставить номер i. Топологический анализ структур В рассмотренных графовых моделях вершины (элементы структуры) и ребра (связи между элементами) задавались исключительно фактом своего существования. Присущие им свойства никак не раскрывались. Рассмотрим некоторые приемы топологического анализа структур. Анализ элементов. При исследовании структуры особое значение имеет выделение элементов, соответствующих изолированным, висячим и тупиковым вершинам графа. Изолированные вершины неинцидентны ни одному из ребер графа, висячие – соответствуют вершинам, в которые нельзя попасть ни из одной другой вершины графа, тупиковые – вершинам, из которых нельзя попасть в другие вершины графа. Пример. Граф на рис.4 содержит изолированную вершину 12, висячие вершины 1-3 и не имеет тупиковых вершин   9 10 11 12        4 5 6 7 8       1 2 3 Рис.4. Граф, содержащий изолированную и висячие вершины Отыскать в графе изолированные, висячие и тупиковые вершины несложно. Для этого достаточно иметь матрицу смежности графа V= , для которой для каждой вершины  , где n-число вершин в графе, определяется вектор  с компонентами:  (4)Согласно уравнениям (4)  есть сумма элементов  й строки, а  - -го столбца матрицы смежности. Величина определяет число ребер, выходящих из вершины , а  - число ребер, входящих в неё. Когда  , вершина -изолированная; при  - тупиковая; при  - висячая.Для рассматриваемого графа получаем следующую матрицу инциденций
Компонентами вектора являются
Компонентами вектора являются
Наличие в графе изолированных вершин ( в примере – вершина 12) обычно свидетельствует об ошибках, допущенных при формировании или описании структуры. Система – это целостный объект, все элементы которого взаимосвязаны. |