Структурный анализ. структ анализ. Методы описания структур
 Скачать 392 Kb. Скачать 392 Kb.
|
|
В структуре с минимальной сложностью (см. рис.9) из каждой висячей вершины можно попасть в тупиковую единственным путем. Для такой структуры Для сложных графов, содержащих большое число путей, непосредственный анализ (как в двух предыдущих случаях ) неприменим. Общий подход, позволяющий вычислить Шаг 1. Исходный граф представляется в виде многоуровневого иерархического графа. Шаг 2. Иерархический граф, получаемый на шаге 1, преобразуется в эквивалентный ему граф, не содержащий смежных вершин, расположенных на одном уровне иерархии. Шаг 3. Полученный в результате граф представляется совокупностью гиперграфов. Шаг 4. Перемножая матрицы инциденций гиперграфов, получаем матрицу W= Пример. Дан граф, представленный на рис.7. Изобразим его в виде иерархического графа, в котором уровень иерархий каждой вершины определяется минимальным числом ребер, связывающих её с висячими вершинами. Получаем граф, представленный на рис.10.который содержит ребра, связывающие вершины одного уровня. 7 5 8           4 3 6          1 2   Рис.10. Преобразованный граф Чтобы избавиться от этих ребер, все инцидентные им вершины продублируем фиктивными вершинами, расположенными на уровень иерархии выше. На рис.11 фиктивные вершины обозначены номерами со штрихом       7 5 8                    4 3 6 4 3 6      2 Рис.11. Граф, содержащий фиктивные вершины. Введение фиктивных вершин позволяет заменить связи между вершинами одного уровня эквивалентными им связями между вершинами соседних уровней иерархии. Так, ребро (3,4) графа на рис.10 заменяется ребром (3, Полученный пятиуровневый иерархический граф описывается четырьмя гиперграфами с матрицами инциденций: 4 3 6 W1= 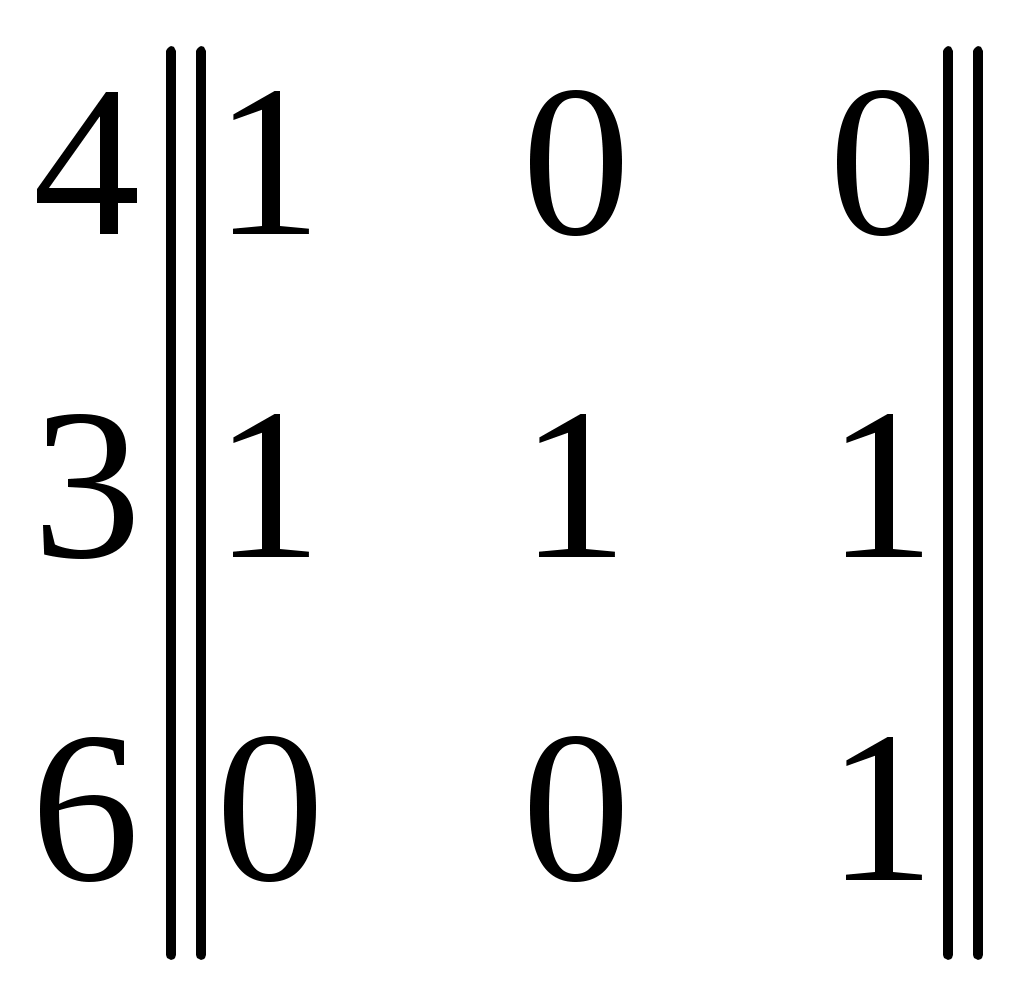 7 5 8 W3= 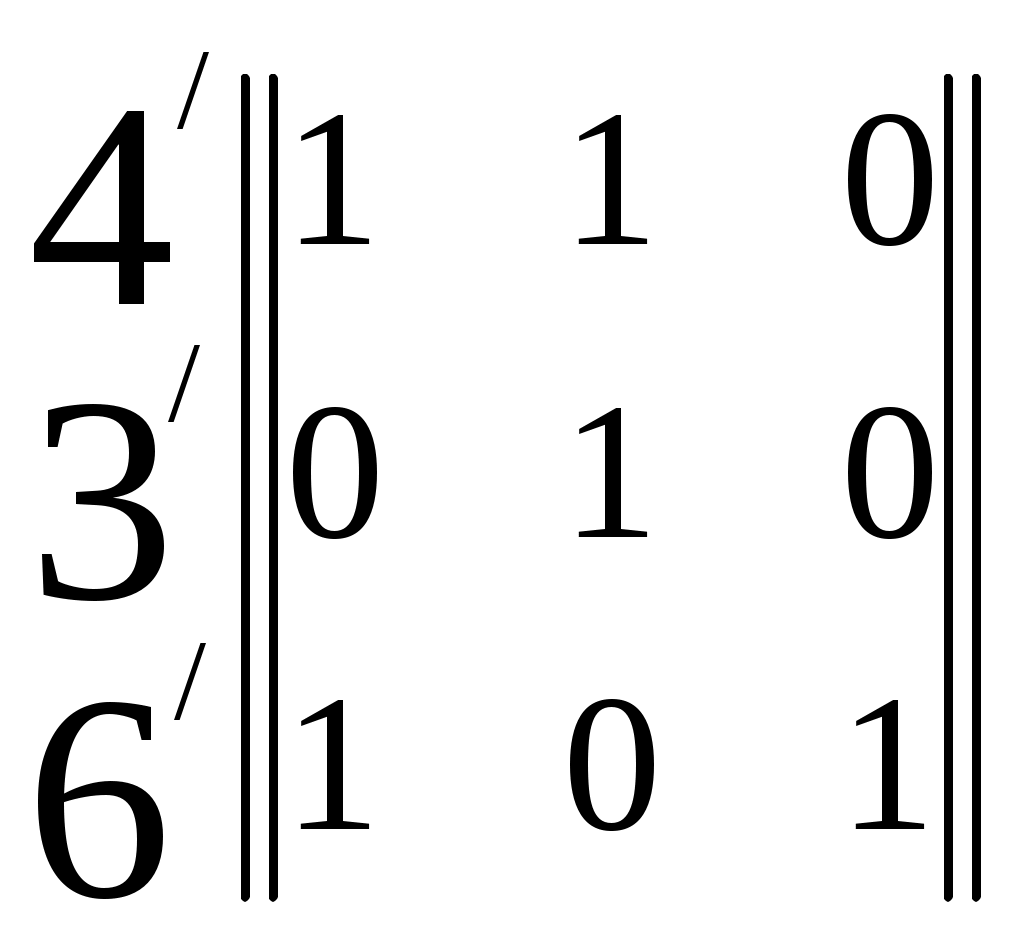 W4= W4=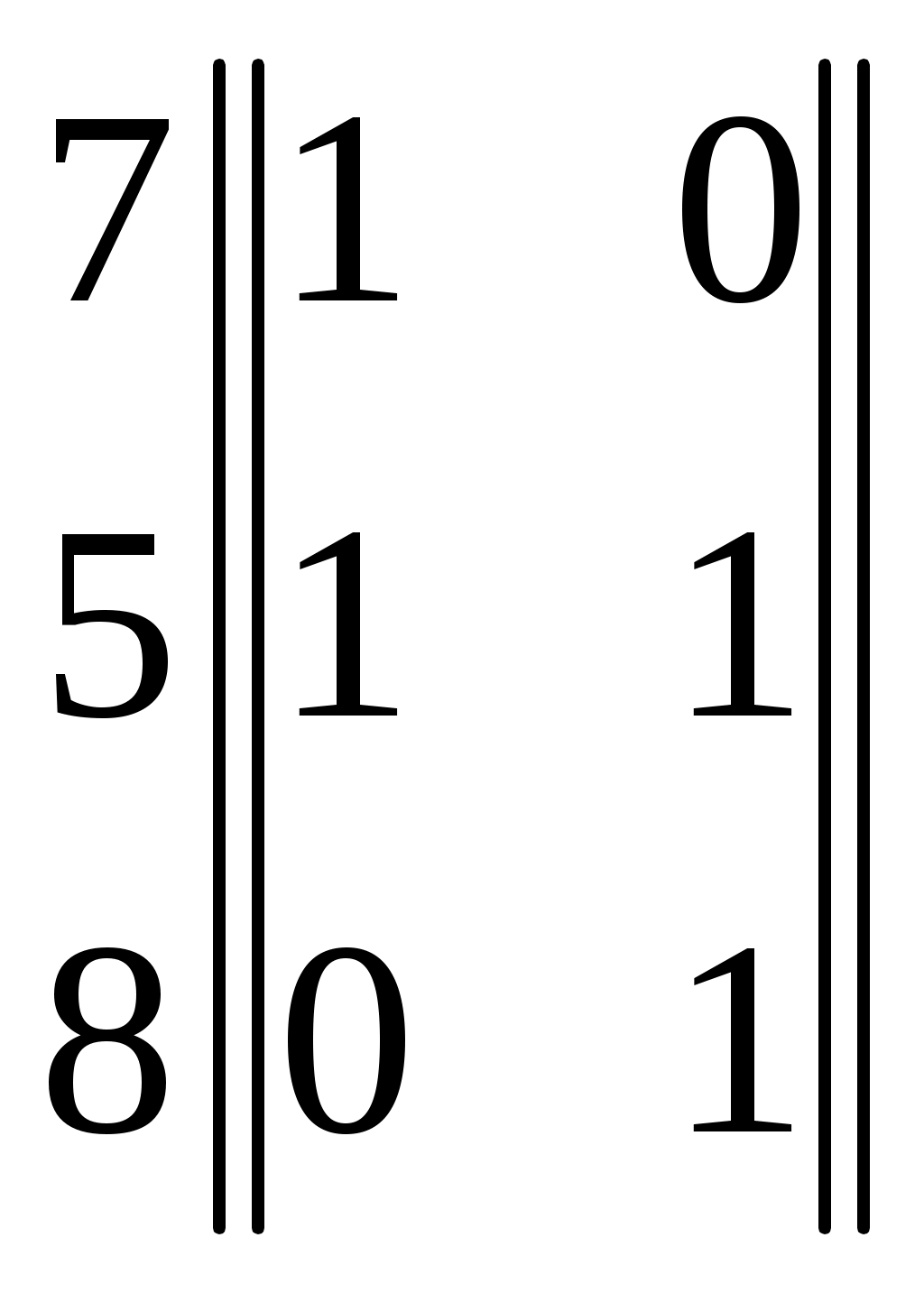 Перемножая эти матрицы, получим 4 3 6 W=W1W2W3W4= 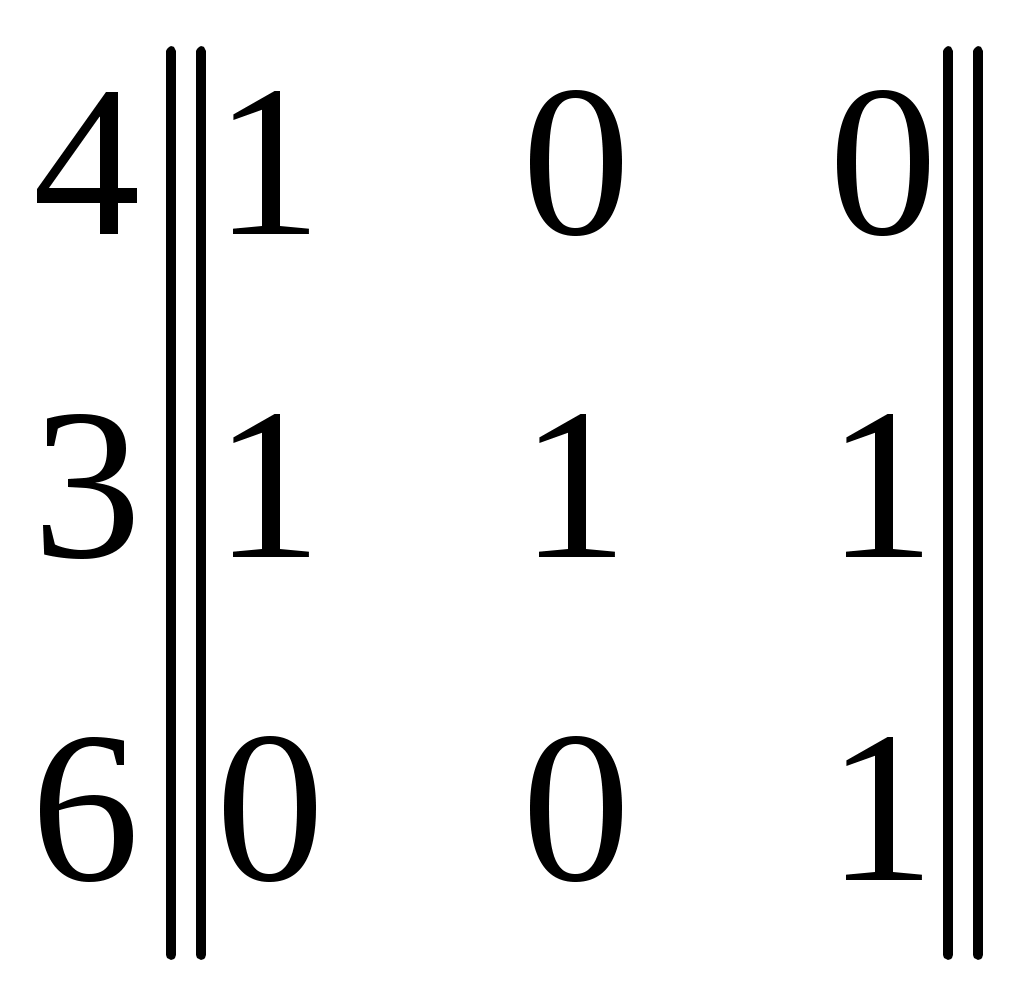 = 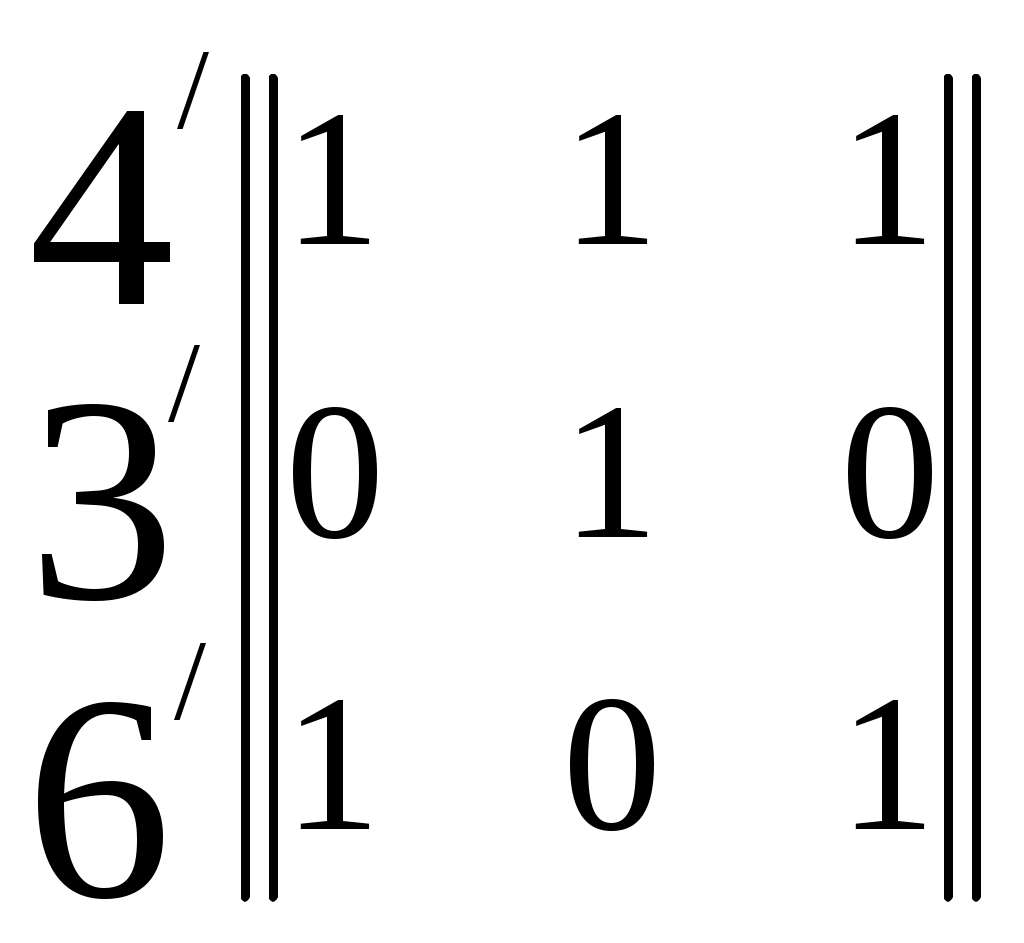 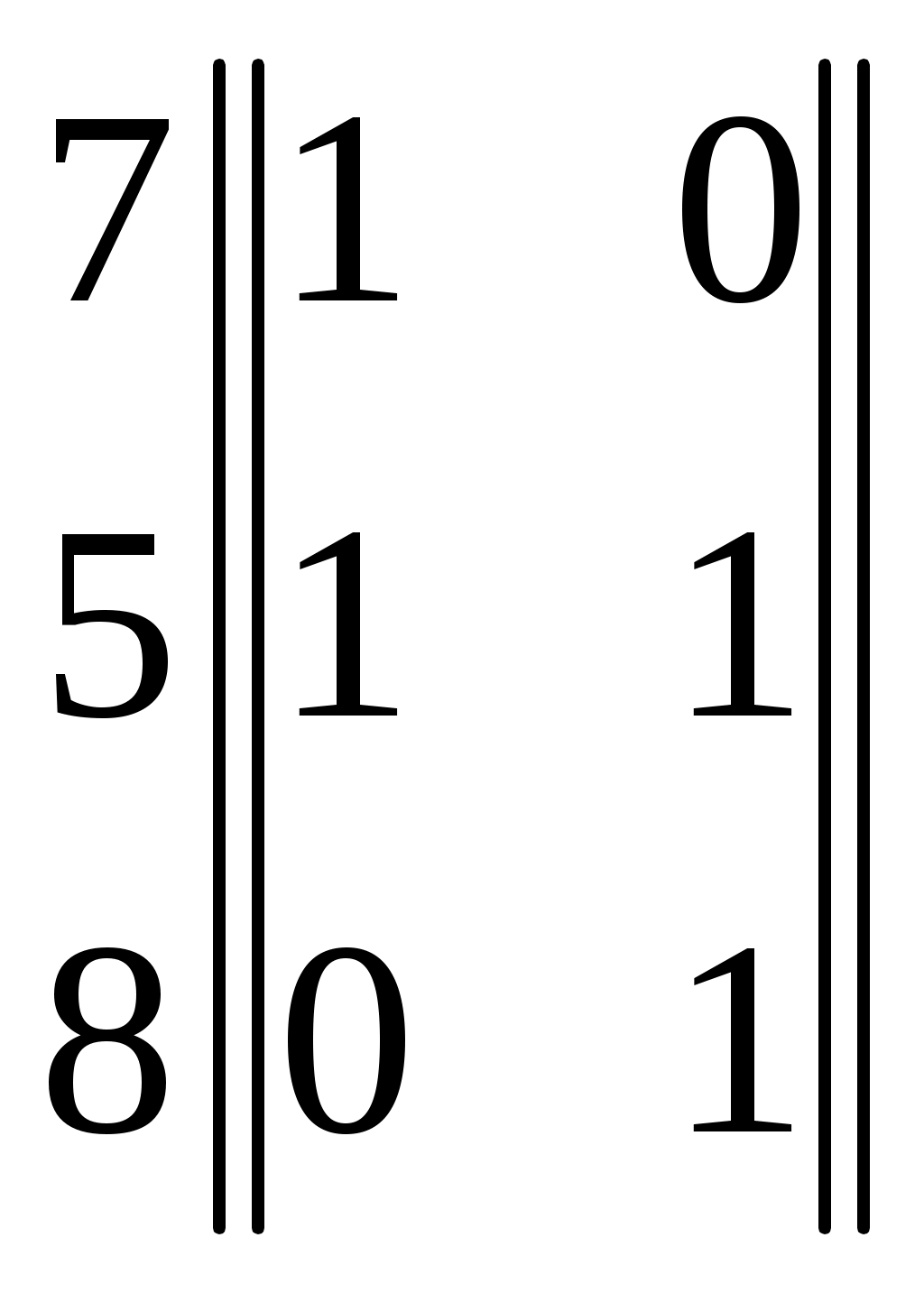 = == Отсюда ясно, что |
