Методы принятия управленческих решений. Методы принятия управленческих решений
 Скачать 368 Kb.
|
|
После пересчета связанных рангов определяется сумма баллов по строкам матрицы и определяется коэффициент значимости. Исходя из суммы баллов и коэффициента значимости можно проранжировать рассмотренные факторы по степени важности: чем меньше сумма баллов, тем важнее фактор. Средний балл за сессию будут выступать как функция: Бср =  .Итак, мы получили следующую последовательность: х4 >-  >- х8 >- х6 >- х5 >- х7 >- х1Вывод: в данном примере наиболее существенными являются факторы х1, х7, х5. 3. Величина этого коэффициента изменяется в пределах от 0 до 1, при чем, если коэффициент приобретает значение 0, то мнение всех экспертов совершенно различно, если 1 - то мнения абсолютно одинаковы. Обычно считается, что если величина коэффициента конкордации превышает 0,5, то полученный результат можно взять за основу и использовать для последующих решений. Если его значение менее 0,5, то необходимо повторить процесс, улучшить состав экспертов. Коэффициент конкордации рассчитывается по следующей зависимости: 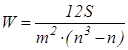 ; 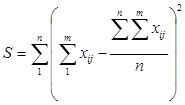При наличии связанных рангов коэффициент W рассчитывается по формуле: 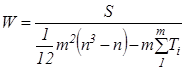 ;  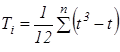, где S – отклонение среднего ранга j-го признака;n – количество экспертов; m – число экспертов; t - число связанных рангов, введенных i-м экспертом; 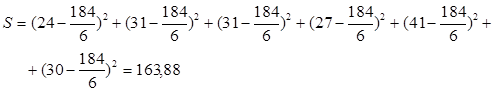 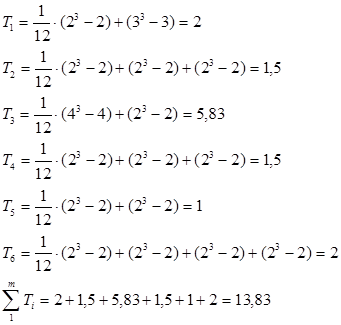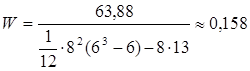- сумма рангов значимости, введенных i-м экспертом (из исходных данных); - общая сумма рангов, введенных экспертами.   Вывод: коэффициент конкордации W<0,5, а следовательно, согласованность в оценках экспертов отсутствует. Недостаток рассмотренного метода заключается в том, что эксперту при ранжировании факторов достаточно сложно ориентироваться в общей их совокупности. Эти недостатки исключает другая модификация метода экспертных оценок - это метод попарного сравнения. 2. Метод попарного сравнения Суть метода состоит в том, что экспертам предлагается сравнить факторы между собой, при этом используется следующая шкала: 1. если фактор xi более значим, чем фактор xj , то это обозначается 1. xi >- xj - [1] 2. если фактор xi менее значим, чем фактор xj , то это обозначается 0. xi -< xj - [0] 3. если фактор xi имеет одинаковую значимость с фактором xj , то это обозначается 0,5. xi¥ xj - [0,5] Суть метода состоит в том, что экспертам предлагается произвести попарную оценку факторов в форме матриц Матрица попарного сравнения факторов, выполненная каждым экспертом
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||