Методы расчета показателей надежности сжат
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
3.Методы расчёта показателей надёжности СЖАТ3.1 Статистические оценки показателей надежности.3.1.1 Построение функции распределения и функции плотности распределения по статистической выборкеСтатистика отказавших реле. Таблица 1 Количество попаданий в интервалы. Таблица 2
Диапазон значений случайной величины ( 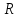 ): ):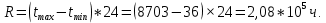 Количество интервалов К: 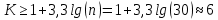 Интервалы 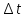 : :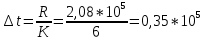 Определение частоты попадания в i-й интервал ( 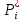 ): ):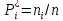 ni - Число попаданий в i-й интервал n - Количество значений в выборке 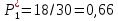 Определим статистическую плотность вероятности безотказной работы ( 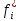 ): ):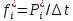 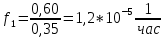 Результаты сведем в таблицу 3 Таблица 3
На основании данных таблицы 3 построим полигон и гистограмму частот (см. рис.1, рис. 2), Далее, используя формулы: 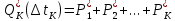 По виду гистограммы, можно предположить экспоненциальный закон распределения времени наработки t. Примем эту гипотезу и проверим степень ее правдоподобия, используя критерий Пирсона. Для этого построим теоретическую функцию частоты отказов, предполагая экспоненциальный закон распределения для времени наработки: 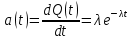 где: 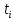 - значение центров интервалов - значение центров интервалов 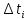 ; ;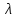 - интенсивность отказов; - интенсивность отказов;Среднее время наработки до отказа ( 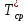 ): ):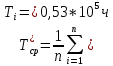 Интенсивность отказов ( 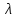 ): ):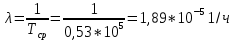 Формула теоретического числа попаданий в i-й интервал ( 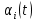 ): ):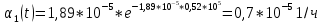 Используя полученное значение интенсивности отказов 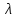 , найдем значения частоты отказов для заданных значений времени наработки , найдем значения частоты отказов для заданных значений времени наработки 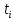 . Эти значения представлены в 7-йстроке таблицы 3. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2 красной линией. . Эти значения представлены в 7-йстроке таблицы 3. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2 красной линией. Далее, найдем теоретическое число попаданий в i-й интервал ( 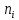 ): ):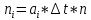 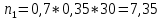 Значения теоретического числа попаданий в i-й интервал ni представлено в 8-й строчке таблицы 3. Мера расхождения между теоретическими числами ni и экспериментальными 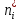 ( (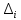 ): ):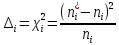 где: 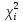 - критерий согласия Пирсона; - критерий согласия Пирсона;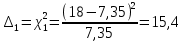 Просуммировав значения этого ряда, найдем значение 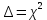 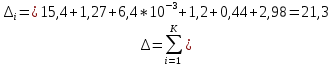 Число степеней свободы: 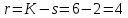 k — число интервалов группирования t Таблица 4 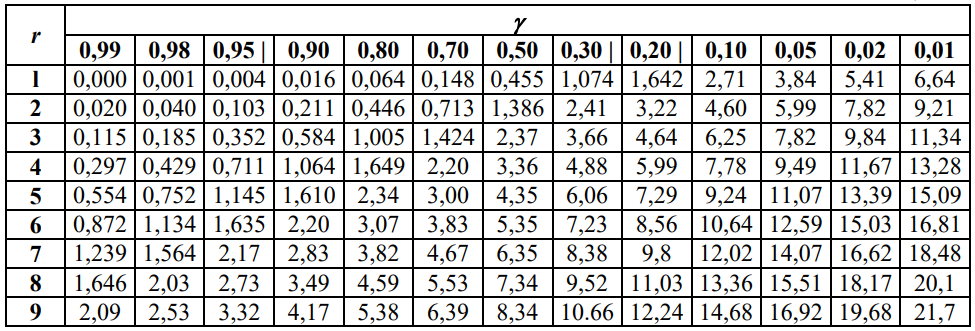 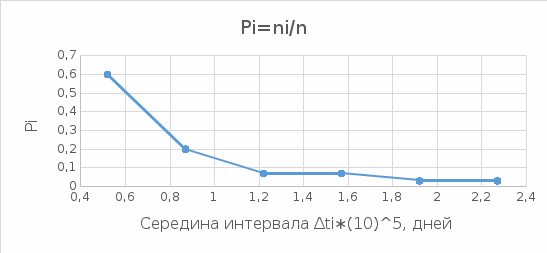 Рис.1 График полигона 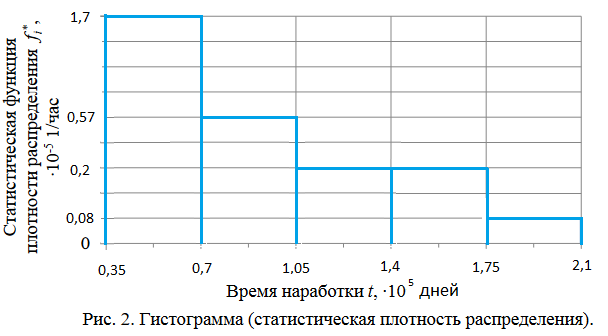 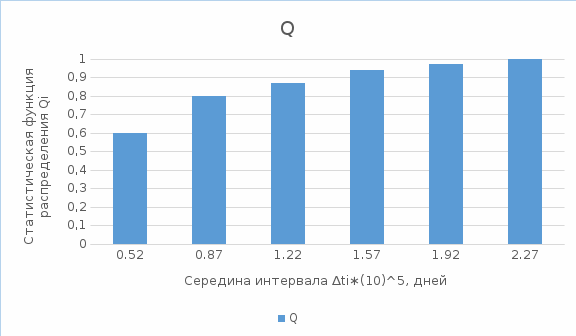 Рис.3. Статистическая функция распределения |

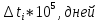
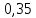
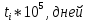
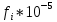 ,1/ч
,1/ч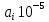 ,1/ч
,1/ч