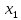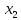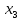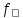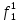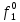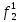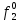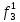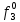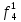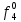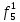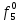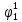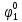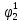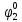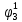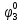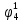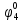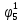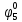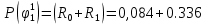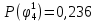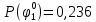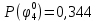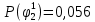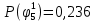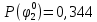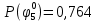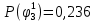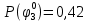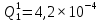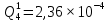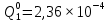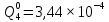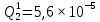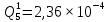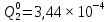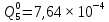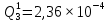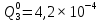Методы расчета показателей надежности сжат

• Название: Методы расчета показателей надежности сжат
• Дата: 23.12.2022
• Размер: 0.5 Mb.
• Имя файла: Gotovaya_kursovaya.docx
• Тип: Курсовая; #861300
• страница: 4 из 8

3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств

Рис.4.

Рисунок 4 – Заданный промежуток времени

Исходные данные, согласно варианту, приведены в таблице 5.

t1, мес	t2, мес	t3, мес	N0, шт	n01, шт	n12, шт	n23, шт	nв01, шт	nв12, шт	nв23, шт
22	44	66	2200	66	66	88	44	66	88

Таблица 5.

Заданный промежуток Δt₀₂= 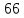. За этот промежуток сгорело n₀₂=132 лампочек, успели восстановить n_в02=110 лампочек.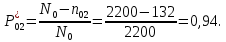



Вероятность отказа: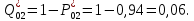



Частоту отказов можно найти по формуле: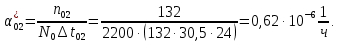



Интенсивность отказов находим по формуле: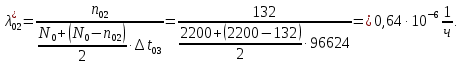


Параметр потока отказов можно оценить по формуле: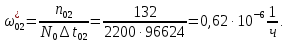



Далее найдем показатели ремонтопригодности.

Вероятность восстановления находим по формуле: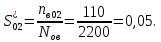



При этом считаем, что число, поставленных на восстановление устройств на начало промежутка N_0В, равно числу неисправных устройств на всем рассматриваемом промежутке.

Частоту восстановления и интенсивность восстановления найдем по формуле: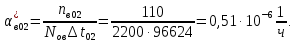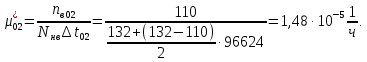

3.2 Расчет надежности комбинационных схем

Логическая функция в алгебраическом виде: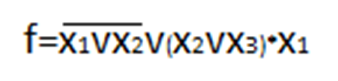



Используя правила синтеза, построим комбинационную схему на двухвходовых логических элементах: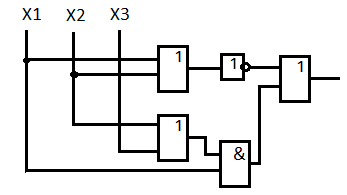



Рис.5. Комбинационная схема на логических элементах

Рассмотрим неисправности на выходе всех логических элементов, входящих в схему:

Таблица 6

S
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	0	0	1	0	1	1	1	1	0	1	1	1	0
1	0	0	1	1	0	1	1	1	1	0	1	1	1	0
2	0	1	0	0	0	1	0	0	1	0	1	0	1	0
3	0	1	1	0	0	1	0	0	1	0	1	0	1	0
4	1	0	0	0	0	1	1	0	1	0	1	0	1	0
5	1	0	1	1	1	1	1	0	1	1	1	0	1	0
6	1	1	0	1	1	1	1	0	1	1	1	0	1	0
7	1	1	1	1	1	1	1	0	1	1	1	0	1	0

S
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	0	0	1	1	0	0	0	0	1	0	0	0	1
1	0	0	1	1	1	0	0	0	0	1	0	0	0	1
2	0	1	0	0	0	1	0	0	1	0	1	0	1	0
3	0	1	1	0	0	1	1	0	1	0	1	0	1	0
4	1	0	0	0	0	1	0	0	1	0	1	0	1	0
5	1	0	1	1	0	0	0	1	0	0	0	1	0	1
6	1	1	0	1	0	0	0	1	0	0	0	1	0	1
7	1	1	1	1	0	0	0	1	0	0	0	1	0	1

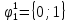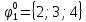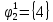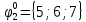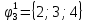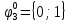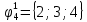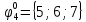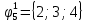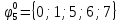Вероятности появления входных переменных 𝑝1= 0,4; 𝑝2= 0,3; 𝑝3= 0,8.

Определим вероятности Rk появления входных наборов и составим таблицу, отражающую полную группу событий на входе схемы:

Таблица 7

S	X1	X2	X3	f	Rk
0	0	0	0	1	R0=(1-0,4)*(1-0,3)*(1-0,8)=0,084
1	0	0	1	1	R1=0,6*0,7*0,8=0,336
2	0	1	0	0	R2=0,6*0,3*0,2=0,036
3	0	1	1	0	R3=0,6*0,3*0,8=0,144
4	1	0	0	0	R4=0,4*0,7*0,2=0.056
5	1	0	1	1	R5=0,4*0,7*0,8=0,224
6	1	1	0	1	R6=0,024
7	1	1	1	1	R7=0,096

Вероятность истинности функции f: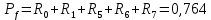



Вероятности истинности функции ошибки:

Вероятность появления неисправности в момент времени t для каждого элемента:

Вероятность ошибки на выходе схемы в момент времени t: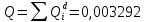



Вероятность исправной работы схемы: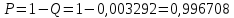