КУрсовая ОТН , системы надежности СЖАТ. Методы расчета показателей надежности сжат
 Скачать 492.17 Kb. Скачать 492.17 Kb.
|
ОглавлениеВведение 7 1.Статистические оценки показателей надежности. 8 2.Расчёт надёжности комбинационных схем 16 5 Топологический метод расчета надежности резервированных систем 31 6.Расчет эксплуатационной надежности СЖАТ 34 Список используемой литературы 37 ВведениеОсобенности надежности и безопасности СЖАТ. Качество перевозочного процесса на жд транспорте определяется быстротой и безопасностью доставки грузов и пассажиров к месту назначения. Оба эти показателя решающим образом зависят от надежности функционирования СЖАТ. Отказы данных систем приводят к задержкам поездов, а в худшем случае, могут приводить к аварийным ситуациям и катастрофам. Обеспечение надежности СЖАТ является задачей разработчиков этих систем и эксплуатационного персонала. Первые должны создавать системы с высоким ресурсом надежности, вторые поддерживать этот ресурс в процессе эксплуатации. Поэтому инженеры СЦБ должны знать основы теории надежности и владеть методами расчета и обеспечения надежности и безопасности систем. Обеспечение высокого уровня безотказности и безопасности СЖАТ является непростой научно-технической проблемой. Трудности ее решения определяют особенности СЖАТ; непрерывный характер работы во времени, длительный срок службы, широкое распространение систем по всей стране, серийное производство систем в больших количествах, сложные климатические, динамические и электромагнитные условия работы. Особое значение имеет проблема доказательства и оценки безопасности СЖАТ. При разработке механических и релейных систем эта проблема в строгой постановке не ставилась. Безопасность устройств обосновывалась простым здравым смыслом, простыми принципами работы и опытом экспертов. В микроэлектронных системах для доказательства безопасности требуются расчеты показателей надежности и безопасности, имитационные, стендовые и эксплуатационные испытания. Они составляют суть сертификационных работ, которые проводятся при создании новых СЖАТ в соответствии с требованием Закона РФ «О федеральном жд транспорте» 1995г.В статье 13 этого Закона записано, что технические средства и механизмы, поставляемые жд транспорту, подлежат обязательной сертификации на соответствие требованиям безопасности движения, охраны труда и экологической безопасности. Теория надежности – это наука, изучающая закономерности отказов технических систем, и располагает методами, позволяющими на основе анализа статистических данных по совокупности одинаковых объектов определять вероятность возникновения отказов объектов в процессе их эксплуатации. Долгое время надежность не измеряли количественно, что затрудняло ее эффективную оценку. Для оценки надежности использовались такие понятия как «высокая надежность», «низкая надежность» и другие качественные определения. Установление количественных показателей надежности и способов их измерения и расчета положило начало научным методам в исследовании надежности. На первых этапах развития теории надежности основное внимание было сосредоточено на сборе и обработке статистической информации об отказах изделий. Далее стали уделять больше внимания причинам отказов и их связям с конструкторско-технологическими факторами, контролю надежности на этапе проектирования и изготовления изделия. Отработка на надежность серийно выпускаемых изделий включает в себя: 1) организацию сбора информации о надежности изделия в процессе эксплуатации (рекламации потребителей, данных сервисных служб и т.д.); 2) анализ информации в целях выявления «слабых звеньев» изделия, лимитирующих его надежность; причин отказов и оценки частоты повторяемости каждого из них; технологических параметров, оказывающих решающее влияние на надежность изделия и его комплектующих; 3) разработку мероприятий по устранению причин наиболее часто повторяющихся отказов. 1.Статистические оценки показателей надежности.Сущность экспериментальной оценки надежности состоит в том, что на основании полученных из опыта ограниченных по объему исходных статистических данных по разработанным методам производится определение фактического возможного значения надежности с заданной точностью и достоверностью. Рассмотрим случайную величину t - время безотказной работы (время наработки до отказа). При эксплуатации или испытаниях изделий в течении определённого времени случайная величина t может принять n различных значений. Совокупность этих значений случайной величины t называется статистической выборкой объёма n. Эта выборка может использоваться для статистической оценки закона распределения случайной величины t. При большом числе n удобнее перейти от статистической выборки к статистическому ряду. На основании статистической выборки из 30 значений построить гистограмму частот. Используя критерий Пирсона, убедиться в экспоненциальном законе распределения времени наработки до отказа t. Построить теоретическую функцию плотности распределения (частоту отказов) α(t).
Таблица 1 Переведем время наработки до отказа в часы, в результате статистика примет следующий вид (таблица 1.1). Таблица 1.1
Статистический ряд для данной выборки, а также номер интервала, в который попадает определенное значение представлены в таблицах 2 и 3. Таблица 2
Таблица 3
Возьмем диапазон значений случайной величины от 2832 до 273192. Диапазон значений случайной величины t: 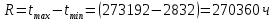 Количество интервалов K (по заданию преподавателя): 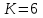 Интервал 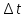 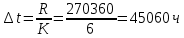 Частота попадания в iй интервал 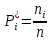 1. 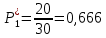 2. 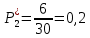 3. 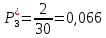 4. 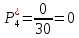 5. 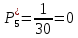 ,033 ,0336. 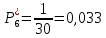 Статистическая плотность вероятности времени безотказной работы (частота отказов  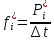 1. 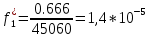 2. 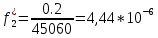 3. 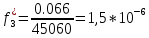 4. 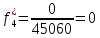 5. 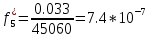 6. 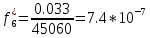 Таблица 4
Построим полигон и гистограмму частот. 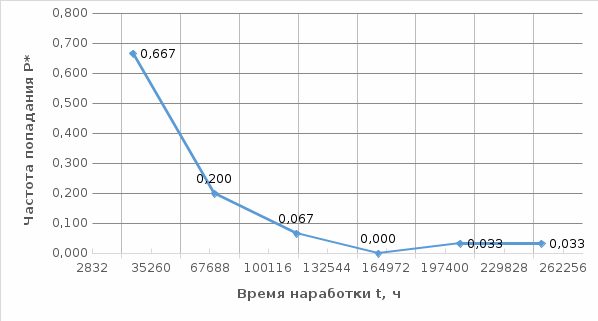 Рис. 1 График полигона (частота попадания в заданный интервал) 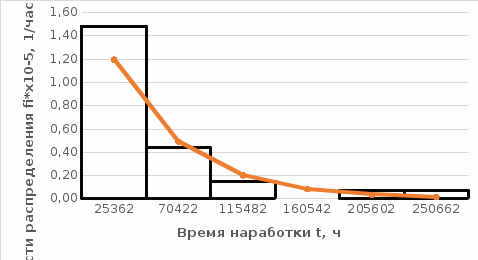 Рис. 2. Гистограмма (статистическая плотность распределения). Построим статистическую функцию распределения Q. 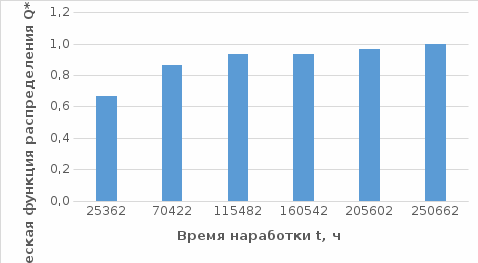 Рис. 3. Статистическая функция распределения. По виду гистограмм можно предположить экспоненциальный закон распределения времени наработки t. Примем эту гипотезу и проверим степень ее правдоподобия, используя критерий Пирсона. Для этого построим теоретическую функцию частоты отказов, предполагая экспоненциальный закон распределения для времени наработки: 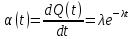 для значений ti –центров интервалов для значений ti –центров интервалов 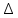 ti, i=1,2,3,4,5 и ti, i=1,2,3,4,5 и 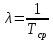 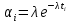 1. 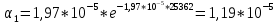 2. 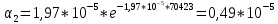 3. 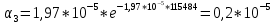 4. 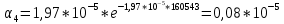 5. 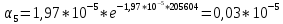 6. 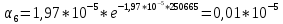 Среднее время наработки до отказа 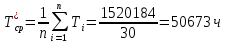 Интенсивность отказов 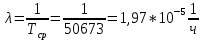 Теоретическое число попаданий в i-ый интервал: 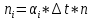 1. 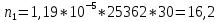 2.  3. 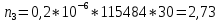 4. 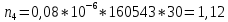 5. 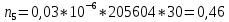 6. 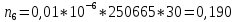 Найдем значения 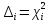 – меры расхождения между теоретическими числами – меры расхождения между теоретическими числами 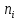 и экспериментальными и экспериментальными 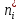 : :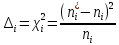 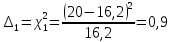 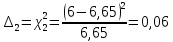 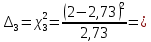 0,196 0,196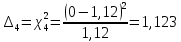 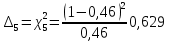 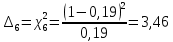 Значения 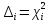 представлены в последней строчке таблицы 4 . представлены в последней строчке таблицы 4 .Просуммировав значения этого ряда, найдем значение 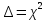 : :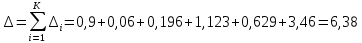 Число степеней свободы 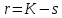 =6-2=4 =6-2=4Для r=4 и 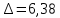 находим вероятность γ=0,2. Это значение не превышает порог γ=0,3, что говорит о согласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. находим вероятность γ=0,2. Это значение не превышает порог γ=0,3, что говорит о согласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

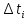 , ч
, ч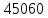
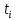 , ч
, ч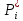
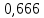
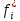 , 1/ч
, 1/ч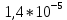
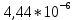
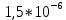
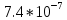
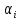 , 1/ч
, 1/ч