КУрсовая ОТН , системы надежности СЖАТ. Методы расчета показателей надежности сжат
 Скачать 492.17 Kb. Скачать 492.17 Kb.
|
|
Среднее время безотказной работы. Система дифференциальных уравнений Колмогорова может быть использована для определения среднего времени безотказной работы (времени наработки до первого отказа), которая является суммой средних времен нахождения системы во всех исправных и работоспособных состояниях. 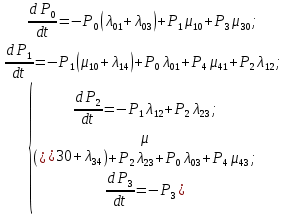 После преобразований Лапласа система примет вид: 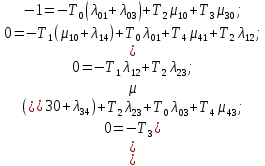 Подставим численные значения: 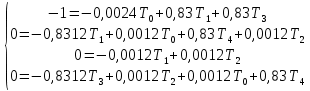 Решим систему уравнений методом Гаусса. (программным способом) В результате получим следующие значения: 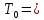 411,985 ч 411,985 ч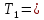 2,34 ч 2,34 ч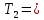 411,985 ч 411,985 ч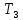 =2,34 ч =2,34 чНайдем среднее время безотказной работы (среднюю наработку до отказа) как сумму времени нахождения системы во всех исправных и работоспособных состояниях. 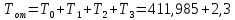 4+411,985+2,34=828,65 (ч) 4+411,985+2,34=828,65 (ч)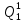 = =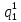 *P( *P(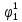 ) = 0,001*0,084 = 0,84*10-4 ) = 0,001*0,084 = 0,84*10-4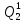 = =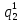 *P( *P(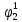 ) = 0,001*0,288 = 2,88*10-4 ) = 0,001*0,288 = 2,88*10-4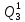 = =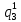 *P( *P(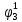 ) = 0,001*0,14 = 1,4*10-4 ) = 0,001*0,14 = 1,4*10-4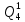 = =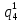 *P( *P(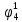 ) = 0,001*0,288 = 2,88*10-4 ) = 0,001*0,288 = 2,88*10-4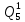 = =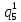 *P( *P(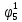 ) = 0,001*0,288 = 2,88*10-4 ) = 0,001*0,288 = 2,88*10-4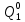 = =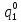 *P( *P(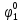 ) = 0,001*0,288 = 2,88*10-4 ) = 0,001*0,288 = 2,88*10-4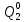 = =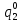 *P( *P(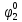 ) = 0,001*0,336 = 3,36*10-4 ) = 0,001*0,336 = 3,36*10-4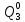 = =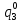 *P( *P(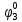 ) = 0,001*0,428 = 4,28*10-4 ) = 0,001*0,428 = 4,28*10-4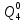 = =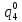 *P( *P(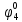 ) = 0,001*0,428 = 4,28*10-4 ) = 0,001*0,428 = 4,28*10-4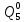 = =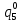 *P( *P(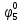 ) = 0,001*0,68 = 6,8*10-4 ) = 0,001*0,68 = 6,8*10-4Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле: Q = ∑ 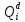 Q = 0,84*10-4 + 2,88*10-4 +1,4*10-4 + 2,88*10-4 + 2,88*10-4 + 2,88*10-4 + 3,36*10-4 + 4,28*10-4 + 4,28*10-4 + 6,8*10-4 = 32,48 *10-4 Вероятность отсутствия ошибки на выходе схемы, то есть вероятность исправной работы равна: P = 1 - Q = 1 – 0,003248 = 0,996752 В разделе по заданной функции алгебры логики была построена комбинационная схема, после чего была рассчитана ее надежность. Вероятность ошибки на выходе схемы в момент времени t равна 32,48 *10-4 вероятность исправной работы схемы 0,996752. 4. Структурный метод расчета надежности Структурная схема расчета надежности (ССРН) - это графическое представление условий, при которых объект находится в работоспособном или неработоспособном состоянии. Элементы, из которых состоит ССРН, означают события, которые могут произойти (с точки зрения надежности) с элементами исследуемого объекта. Например, элемент электрической схемы - резистор может быть в работоспособном состоянии (событие А) или неработоспособном состоянии (событие В). В неработоспособное состояние он может перейти в результате обрыва (событие 1) или короткого замыкания (событие 2) резистора. Элементы ССРН могут включаться последовательно или параллельно. Последовательно они соединяются, если каждое событие (например, 1 или 2) ведет к отказу объекта. Параллельно элементы ССРН соединяются в случаях, когда к отказу объекта ведет совместное наступление всех событий, учитываемых при расчете надежности. Численные значения параметров надежности объекта могут быть определены, если заменить события, учтенные при анализе и вошедшие в ССРН, на вероятности этих событий. Элементы ССРН могут образовывать простые и сложные узлы. Простой узел образуется из одного или k - элементов, включенных параллельно. Сложные узлы образуются из параллельно-последовательного соединения, в котором в одной из параллельных ветвей последовательно включено несколько элементов. Расчет надежности сложного узла выполняется, начиная с последовательного соединения элементов. 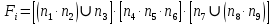 На рисунке 1 представлена структурная параллельно-последовательная схема для расчета надежности.  Рис.1 Составим логическую функцию 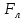 описания работы системы: описания работы системы: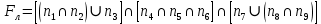 Арифметическая функция 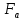 описания работы системы будет выглядеть следующим образом: описания работы системы будет выглядеть следующим образом: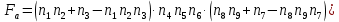 Интенсивность отказов каждого элемента 𝝀i (1/ч) и время восстановления узла Tву (час) определены следующим образом: 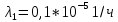 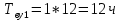 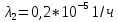 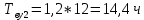 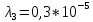 1/ч 1/ч 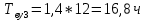 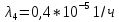 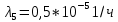 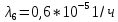 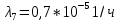 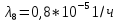 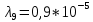 1/ч 1/чОсновные формулы: «И» 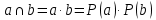 «ИЛИ» 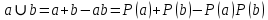 «НЕ» 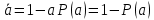 Рассмотрим последовательное соединение элементов (рис. 2), для него справедливы следующие формулы: 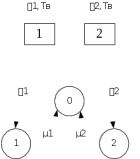 Рис. 2 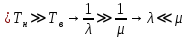 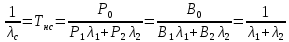 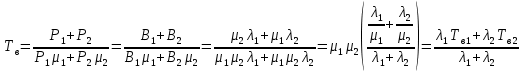 Таким образом: 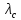 = =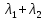 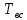 = =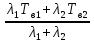 *Если 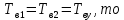 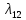 = =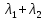 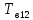 = =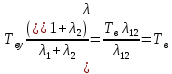 Для параллельного соединения элементов (рис.3) справедливы следующие формулы:  Рис.3 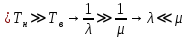 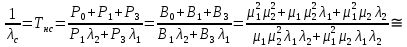 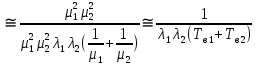 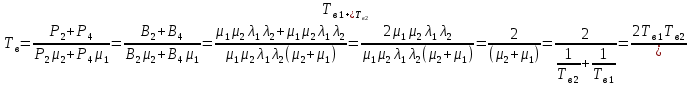 Таким образом: 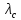 = =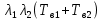 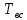 = =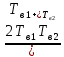 *Если 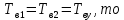 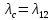 = =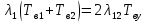 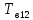 = =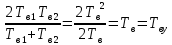 Вероятность безотказной работы системы рассчитаем по формуле: 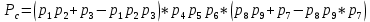 Вероятности безотказной работы элементов равны соответственно: 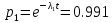 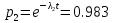 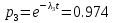 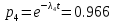 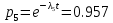 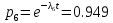 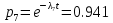 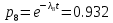 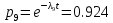 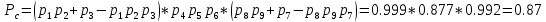 Вероятность отказа системы равна соответственно: 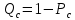 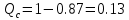 Рассмотрим 1 узел. Преобразуем его к последовательному виду.  Рис.4 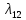 = =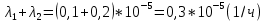 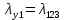 = =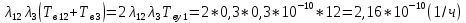 Рассмотрим 2 узел. Преобразуем его к последовательному виду.  Рис.5 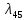 = =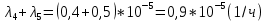 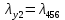 = =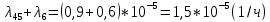 Рассмотрим 3 узел. Преобразуем его к последовательному виду.  Рис.6 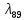 = =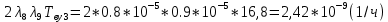 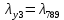 = =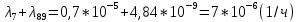 Интенсивность отказов для системы: 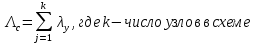 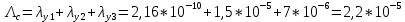 (1/ч) (1/ч)Среднее время работы системы на отказ: 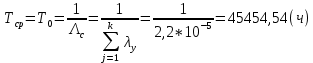 Среднее время восстановления системы: 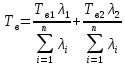 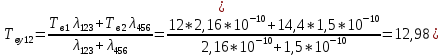 ч) ч)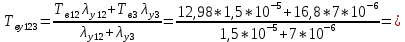 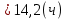 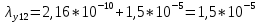 (1/ч) (1/ч)Коэффициент готовности: 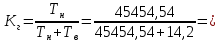 0,999688 0,999688Ответ: 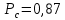 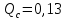 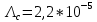 (1/ч) (1/ч)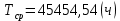 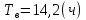 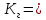 0,999 0,9995 Топологический метод расчета надежности резервированных систем Топологическими называются методы, которые позволяют определить показатели надежности либо по графу состояний, либо по структурной схеме системы без составления и решения уравнений. Как и любые другие методы расчета надежности, они имеют свои ограничения: - интенсивности отказов и восстановления элементов сложной системы являются величинами постоянными, другими словами, время наработки на отказ и время восстановления распределены по экспоненциальному закону; - топологические методы нельзя использовать для многосвязных графов. Пусть дана некоторая система, состоящая из трех последовательно включенных блоков. 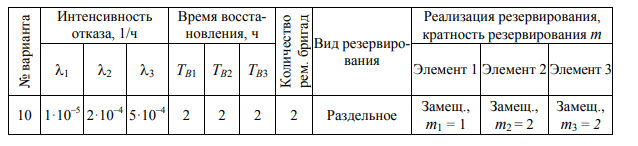 Исходные данные: Исходные данные:П  Рис.1 – Структурная схема системы Построена структурная схема системы после резервирования:  Рис. 2 – Структурная схема после резервирования Определение времени наработки на отказ системы без резервирования. Для экспоненциального закона распределения интенсивностей отказов и восстановлений получено: 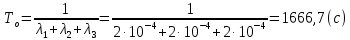 Определение интенсивности отказа первого элемента после резервирования 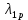 . .Интенсивность переходов 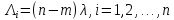 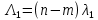 =(6-0) =(6-0)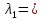 6 6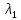 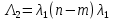 =(6-1) =(6-1)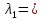 5 5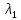 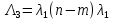 =(6-2) =(6-2)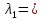 4 4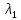 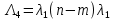 =(6-3) =(6-3)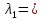 3 3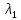  Рис.3 – Граф состояний резервированной системы 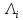 – интенсивности переходов, соответствующие отказам элементов системы, i = 1, 2…; – интенсивности переходов, соответствующие отказам элементов системы, i = 1, 2…;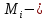 интенсивность переходов, соответствующих восстановлениям элементов системы. интенсивность переходов, соответствующих восстановлениям элементов системы.Интенсивности восстановления 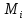 вычисляются по формуле: вычисляются по формуле: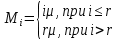 , где r – число ремонтных бригад, r = 2. , где r – число ремонтных бригад, r = 2.Так как обслуживанием занимается одна ремонтная бригада, имеем: 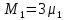 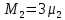 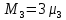 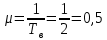 Время наработки на отказ определяется как: 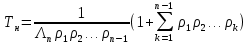 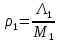 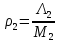 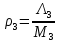 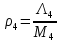 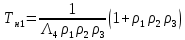 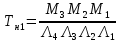 (1+ (1+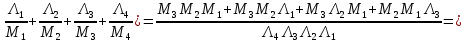 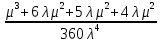 = =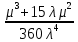 Учитывая экспоненциальный закон распределения интенсивностей переходов, найдём интенсивность отказа резервирования элемента 1: 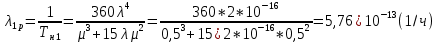 Аналогично интенсивность отказа и интенсивность восстановления для элемента 2 и 3. 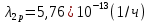 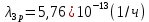 Найдём время наработки на отказ системы с резервированием: Для экспоненциального закона распределения получим: 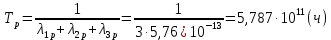 Выигрыш в надёжности по времени наработки на отказ будет: 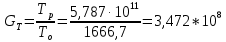 |
