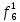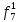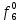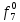КУрсовая ОТН , системы надежности СЖАТ. Методы расчета показателей надежности сжат
 Скачать 492.17 Kb. Скачать 492.17 Kb.
|
|
Статистическая оценка параметров надежности восстанавливаемых устройств. На предприятии в момент времени t0=0 было установлено N0 восстанавливаемых устройств. При проверках на промежутках времени 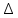 ti(i+1) (i=0,1,2) подсчитывалось, сколько устройств отказало на данном промежутке ni(i+1) и сколько было восстановлено nвi(i+1). (табл.) ti(i+1) (i=0,1,2) подсчитывалось, сколько устройств отказало на данном промежутке ni(i+1) и сколько было восстановлено nвi(i+1). (табл.)Таблица
Найти статистические параметры безотказности и ремонтопригодности на промежутке времени 𝜟t03 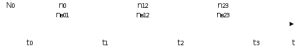 Статистические оценки параметров безотказности Вероятность безотказной работы 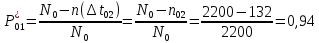 Вероятность отказа 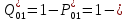 0,94=0,06 0,94=0,06Частота отказов 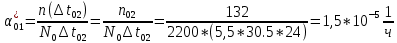 Интенсивность отказов 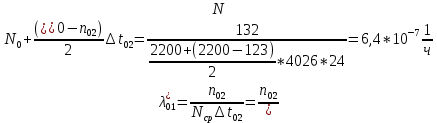 Параметр потока отказов 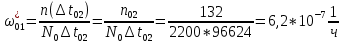 Статистические оценки параметров ремонтопригодности Вероятность восстановления 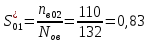 Считаем, что число поставленных на восстановление устройств на начало промежутка 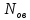 ,равно числу неисправных устройств на всем рассматриваемом промежутке. ,равно числу неисправных устройств на всем рассматриваемом промежутке.Частота восстановления 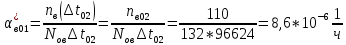 Интенсивность восстановления 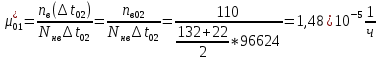 2.Расчёт надёжности комбинационных схем Комбинационная схема – это логическая схема, состояние выходов которой однозначно зависит от состояния входов. Комбинационная схема может быть реализована на разных элементах дискретного действия. Рассмотрим случай синтеза комбинационных схем на двухвходовых логических элементах по следующим правилам синтеза: – каждая логическая схема реализуется соответствующим логическим элементом: 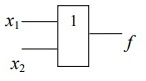 а) функция сложения реализуется элементом ИЛИ 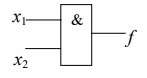 б) функция умножения реализуется элементом И 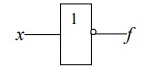 в) функция отрицания реализуется элементом НЕ Функции реализуются в последовательности НЕ, И, ИЛИ. Исходные данные для расчёта могут быть заданы либо в виде функции алгебры логики (ФАЛ), либо в виде логической схемы. Логическая функция задана в алгебраическом виде: 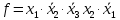 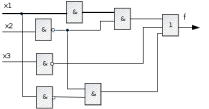 Рисунок 1. Комбинационная схема на двухвходовых логических элементах Таблица 1. Таблица истинности
Таблица 2. Функции, реализуемые схемой при неисправности
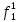 = 0 = 0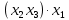 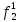 = 1 = 1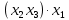 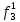 = = 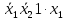 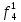 = = 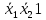 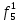 = 1 = 1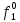 = 1 = 1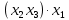 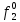 = 0 = 0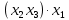 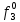 = = 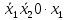 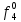 = = 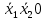 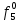 = 0 = 0Таблица 3. Функции ошибки
Функция ошибки в десятичном виде: 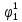 = {1}=1 = {1}=1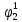 = {0,2,3,4}=1 = {0,2,3,4}=1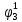 = {0,4}=1 = {0,4}=1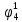 = {0,2,3,4}=1 = {0,2,3,4}=1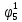 = {0,2,3,4}=1 = {0,2,3,4}=1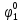 = {0,2,3,4}=1 = {0,2,3,4}=1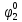 = {1}=1 = {1}=1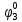 = {0,5,6,7}=1 = {0,5,6,7}=1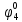 = {0,5,6,7}=1 = {0,5,6,7}=1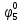 = {1,5,6,7}=1 = {1,5,6,7}=1Функция ошибки в алгебраическом выражении: 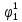 = = 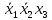 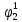 = =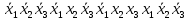 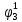 = = 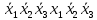 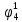 = =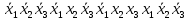 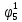 = =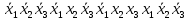 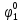 = = 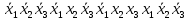 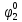 = = 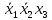 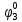 = = 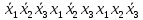 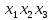 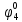 = = 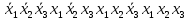 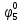 = =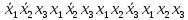 p1, p2 и p3 – вероятности, того что в момент времени t входная переменная xj=1, соответственно (1- pj) – вероятность того, что xj=0. p1 = 0,4, p2 = 0,3, p3 = 0,8 Таблица 4. Вероятность появления входных наборов.
Определим вероятность истинности функции f как сумму вероятностей разрешенных наборов, то есть таких, на которых функция f равна 1: Pf = ∑Rkf Pf = R1 + R5 + R6 + R7 Pf = 0,336 + 0,224 + 0,024 + 0,096 = 0,68 Определим вероятность функции ошибки как сумму вероятностей, того, что на выходе схемы происходит ошибка при наличии сбоя: P( 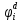 ) = ∑Rkf ) = ∑RkfP( 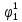 ) = R0 = 0,084 ) = R0 = 0,084P( 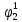 ) = R0 + R2 + R3 + R4 = 0,084 + 0,036 + 0,144 + 0,024 = 0,288 ) = R0 + R2 + R3 + R4 = 0,084 + 0,036 + 0,144 + 0,024 = 0,288P( 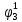 ) = R0+ R4 = 0,084 + 0,056 = 0,14 ) = R0+ R4 = 0,084 + 0,056 = 0,14P( 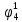 ) = R0 + R2 + R3 + R4 = 0,288 ) = R0 + R2 + R3 + R4 = 0,288P( 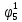 ) = R0 + R2 + R3 + R4 = 0,288 ) = R0 + R2 + R3 + R4 = 0,288P( 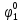 ) = R0 + R2 + R3 + R4 = 0,288 ) = R0 + R2 + R3 + R4 = 0,288P( 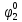 ) = R1 = 0,336 ) = R1 = 0,336P( 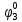 ) = R0 + R5 + R6 + R7 = 0,084 + 0,224 + 0,024 + 0,096 = 0,428 ) = R0 + R5 + R6 + R7 = 0,084 + 0,224 + 0,024 + 0,096 = 0,428P( 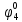 ) = R0 + R5 + R6 + R7 = 0,084 + 0,224 + 0,024 + 0,096 = 0,428 ) = R0 + R5 + R6 + R7 = 0,084 + 0,224 + 0,024 + 0,096 = 0,428P( 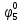 ) = R1+ R5 + R6 + R7 = 0,336 + 0,224 + 0,024 + 0,096 = 0,68 ) = R1+ R5 + R6 + R7 = 0,336 + 0,224 + 0,024 + 0,096 = 0,68Вероятность того, что произойдет неисправность, которая приведет к ошибке на выходе схемы: 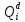 = = 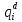 * P( * P(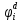 ) )3. Расчет показателей надежности восстанавливаемых систем методом марковских процессов. Работа некоторого устройства характеризуется графом, представленным на рисунке 1. При этом, S0 – исправное состояние, S1, S2, S3 – работоспособные состояния с различными неисправностями, S4 – неработоспособное состояние (состояние отказа). Вероятности переходов между состояниями характеризуются интенсивностями отказов 𝝀ikи интенсивностями восстановления μki. Исходя из заданных значений интенсивностей отказов 𝝀ikи интенсивностей восстановления μki, найти параметры надежности (предполагая простейший поток отказов): 1) финальные вероятности нахождения системы во всех состояниях, в том числе вероятность отказа системы Qс; 2) среднее время наработки на отказ Тсри интенсивность отказов системы 𝝀с; 3) среднее время восстановления Тв; 4) коэффициент готовности Кг; 35 25 15 15 10 5) среднее время безотказной работы (среднюю наработку до отказа) Тот. 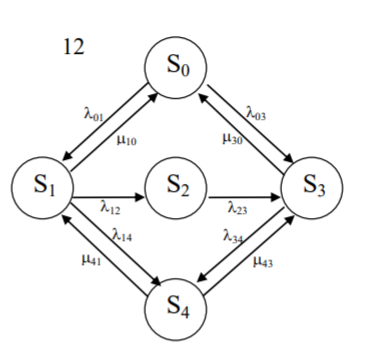 Рис. 1. Выбор численных параметров 𝝀ik =𝝀=12*10-4 1/ч μki = μ=0,83 1/ч Решение Исходя из графа, система может находиться в одном из 5 состояний: 0 – исправное состояние; 1 – 1-е работоспособное состояние: отказал первый элемент (находится в ремонте), второй, третий – исправен; 2 - 2-е работоспособное состояние: отказал второй элемент (находится в ремонте), первый, третий – исправен; 3 - 3-е работоспособное состояние: отказал третий элемент (находится в ремонте), первый, второй – исправен; 4 – неработоспособное состояние (состояние отказа): отказали последовательно три элемента и находятся в состоянии ремонта. Систему дифференциальных уравнений можно записать в виде: 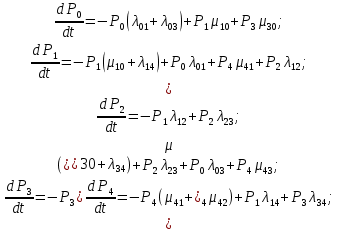 Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях. (алгебраическая форма) 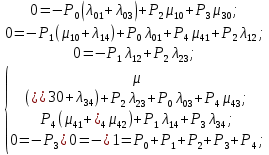 Подставим численные значения: 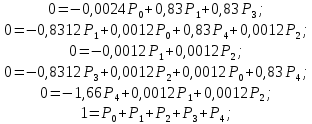 Решим систему уравнений методом Гаусса. (программным способом) В результате получим следующие значения: 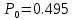 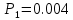 2 2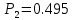 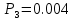 2 2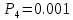 4 4Найдем вероятность отказа системы и вероятность безотказной работы: 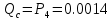 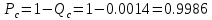 Наработка на отказ может быть вычислена по формуле: 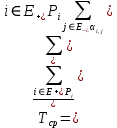 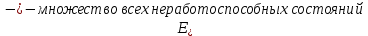 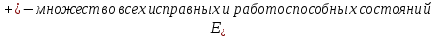 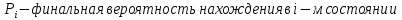 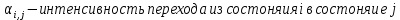 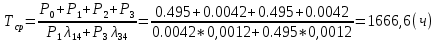 Интенсивность отказов системы 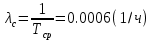 Среднее время восстановления системы может быть вычислено по формуле: 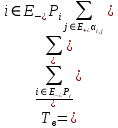 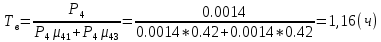 Коэффициент готовности вычисляется по формуле: 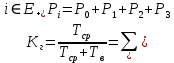 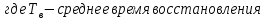 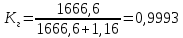 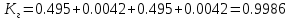 |