Статья 8. Исаев М.И. - Методы сортировки одномерных массивов. Методы сортировки одномерных массивов
 Скачать 38.84 Kb. Скачать 38.84 Kb.
|
|
УДК: 004 Исаев Мовлади Исаевич преподаватель кафедры «Прикладная математика и компьютерные технологии» институт математики, физики и информационных технологий ФГБОУ ВО «Чеченский государственный университет им. А.А. Кадырова» movladi.isaev@yandex.ru Дадахаев Ибрагим Русланович студент 4 курса направления подготовки «прикладная математика и информатика» институт математики, физики и информационных технологий ФГБОУ ВО «Чеченский государственный университет им. А.А. Кадырова» Алдамов Алихан Исмаилович студент 3 курса направления подготовки «математика» институт математики, физики и информационных технологий ФГБОУ ВО «Чеченский государственный университет им. А.А. Кадырова» г. Грозный Isaev Movladi Isaevich teacher of the Department of Applied Mathematics and Computer Technologies Institute of Mathematics, Physics and Information Technologies Chechen State University named after A.A. Kadyrov movladi.isaev@yandex.ru Dadahaev Ibragim Ruslanovich 4rd year student of the direction of training "Applied Mathematics and Informatics" Institute of Mathematics, Physics and Information Technologies Chechen State University named after A.A. Kadyrov AldamovAlikhanIsmailovich 3nd year student of the direction of training "mathematics" Institute of Mathematics, Physics and Information Technologies Chechen State University named after A.A. Kadyrov Методы сортировки одномерных массивов Sorting methods for one-dimensional arrays Аннотация Ниже описан основной алгоритм простых вставок, который порождает несколько модификаций, используемых в заданиях. Алгоритм использует прием, которым пользуются игроки в карты при сортировке только что розданной колоды: очередная карта вставляется между уже упорядоченными ранее. Аnnotation The basic algorithm for simple insertions is described below, which generates several modifications used in the tasks. The algorithm uses a technique that card players use when sorting a deck that has just been dealt: the next card is inserted between the previously ordered ones. Ключевые слова: метод сортировки, массивы, одномерные массивы Key words: sort method, arrays, one-dimensional arrays Файл, подлежащий сортировке, в общем случае состоит из элементов-записей, включающих информационную часть и ключи, по которым производится упорядочение по возрастанию. Поскольку информационная часть почти не влияет на процесс сортировки, будем предполагать, что файлы, используемые в примерах, состоит только из элементов-ключей, а информационная часть записи отсутствует. Здесь k[1], k[2], ... , k[N] - ключи, по которым производится упорядочение файла. X,i,j - рабочие переменные. 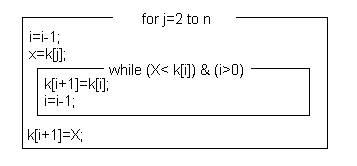 Рис.1. Алгоритм простых вставок Для примера возьмем файл, состоящий из 8 элементов: Исх.файл.: 503 87 512 61 908 170 897 275 Алгоритм будет преобразовывать его следующим образом: j=2. Исх : 503 87 X=87 Рез : °87 503 j=3 : 87 503 °512 X=512 j=4 : °61 87 503 512 X=61 j=5 : 61 87 503 512 °908 X=908 j=6 : 61 87 °170 503 512 908 X=170 j=7 : 61 87 170 503 512 °897 908 X=897 j=8 : 61 87 170 °275 503 512 897 908 X=275 Время работы алгоритма t примерно оценивается формулой: t=a*N + b*N, где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Бинарные вставки Для ускорения числа сравнений при поиске места, в которое нужно вставить элемент X, можно использовать логарифмический поиск. Это означает, что сначала Х сравнивается с элементом k[j/2], затем, в зависимости от результата сравнения, с элементом, лежащим посередине между 1 и j/2 или посередине между j/2+1 и j и т.д. При этом число сравнений для каждого j равно примерно log(j). Число пересылок элементов при этом не изменяется и остается примерно равным N/4. Время работы алгоритма t примерно оценивается формулой: t=a*N + b*N + c*N*logN, где a,b,c - неизвестные константы, зависящие от программной реализации алгоритма, log - логарифм по основанию 2. Двухпутевые вставки Число пересылок можно сократить примерно в 2 раза до N/8, если допустить сдвиги элементов не только вправо, но и влево. Для выходного файла резервируется место в памяти, равное 2N+1 ,где N - число элементов в исходном файле. Первый элемент пересылается в середину выходного файла. В дальнейшем элементы выходного файла сдвигаются вправо или влево в зависимости от того, в какую сторону нужно сдвигать меньше элементов. Файл из предыдущего примера будет сортироваться следующим образом. Исх.файл.: 503 87 512 61 908 170 897 275 503 нач. состояние °87 503 Х=87 87 503 °512 Х=512 °61 87 503 512 Х=61 61 87 503 512 °908 Х=908 61 87 °170 503 512 908 Х=170 61 87 170 503 512 °897 908 Х=897 61 87 170 °275 503 512 897 908 Х=275 Из таблицы видно, что присоединение новых элементов к выходному файлу происходит как справа, так и слева от центрального элемента 503 с возможным сдвигом вправо или влево. Время работы алгоритма t примерно оценивается формулой: t=a*N+b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Вставки одновременно нескольких элементов Модификация метода простых вставок заключается в том, что вместо одной переменной Х можно использовать несколько переменных Х1, Х2, ... Xm, которые имеют значения элементов, подлежащих вставке в уже упорядоченную часть файла. Х1, X2, ... Xm упорядочены по возрастанию, поэтому сравнивая Xm в цикле по переменной i с элементами упорядоченной части, мы можем гарантировать, что, если очередной элемент k[i] больше Xm, то он больше и остальных элементов. Перенос элементов исходного файла вперед в цикле по i выполняется на m элементов, то есть вместо k[i+1]=k[i] в исходном алгоритме в модифицированном алгоритме записывается k[i+m]=k[i]. При нахождении k[i] такого, что он меньше Хm, Хm ставится на место k[i+m] и m уменьшается на 1. Далее цикл по i продолжается с новым m. Экономия числа переносов элементов достигается за счет переносов сразу на m элементов. Время работы алгоритма t примерно оценивается формулой: t=a*N + b*N + c*N*logN, где a,b,c - неизвестные константы, зависящие от программной реализации алгоритма. Вставки с убывающим шагом (метод Шелла) Идея алгоритма состоит в обмене элементов, расположенных не только рядом, как в алгоритме простых вставок, но и далеко друг от друга, что значительно сокращает общее число операций перемещения элементов. Для примера возьмем файл из 16 элементов. Сначала просматриваются пары с шагом 8. Это пары элементов 1-9, 2-10, 3-11, 4-12, 5-13, 6-4, 7-15, 8-16. Если значения элементов в паре не упорядочены по возрастанию, то элементы меняются местами. Назовем этот этап 8-сортировкой. Следующий этап - 4-сортировка, на котором элементы в файле делятся на четверки: 1-5-9-13, 2-6-10-14, 3-7-11-15, 4-8-12-16. Выполняется сортировка в каждой четверке. Сортировка может выполняться методом простых вставок. Следующий этап - 2-сортировка, когда элементы в файле делятся на 2 группы по 8: 1-3-5-7-9-11-13-15 и 2-4-6-8-10-12-14-16. Выполняется сортировка в каждой восьмерке. Наконец весь файл упорядочивается методом простых вставок. Поскольку дальние элементы уже переместились на свое место или находятся вблизи от него, этот этап будет значительно менее трудоемким, чем при сортировке вставками без предварительных "дальних" обменов. Для данного примера результаты представлены в следующей таблице. Исходный файл. На нем выполняется 8-сортировка. Пары для возможного обмена соединены одинарными или двойными линиями. Двойными линиями обозначены пары, в которых произошел обмен. 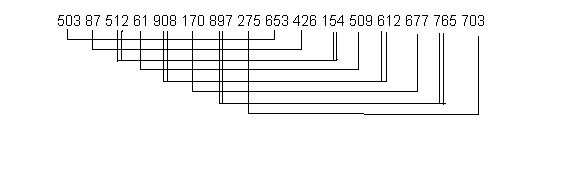 Рис.2. Исходный файл Файл после 8-сортировки. Линиями соединены четверки для следующего этапа. 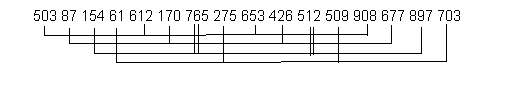 Рис.3. Исходный файл после 8-сортировки Файл после 4-сортировки. Линиями соединены восьмерки для следующего этапа. 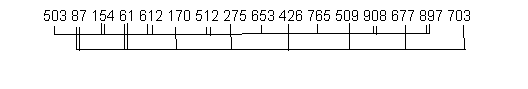 Рис.4. Исходный файл после 4-сортировки Файл после 2-сортировки: 154 61 503 87 512 170 612 275 653 426 765 509 897 677 908 703. Файл после окончательной сортировки (1-сортировки): 61 87 154 170 275 426 503 509 512 612 653 677 703 765 897 908 Время работы алгоритма t примерно оценивается формулой: t=a*N**b, где a и b - неизвестные константы, зависящие от программной реализации алгоритма. . Литература 1. Вирт Н.. Алгоритмы и структуры данных. 1997. 2. Алексеев Е.Р, Чеснокова О.В. Турбо Паскаль 7.0. 1994. 3. Интернет http://ru.wikipedia.org "Википедия" - универсальная энциклопедия. 1994. 4. Интернет http://informatics.mccme.ru Дистанционная подготовка по информатике 5. Либерман М. Алгоритмы сортировки массивов. М.: Наука, 1997. 6. Нортон П., Уилтон Р. 1ВМ РС РЗ/2. Руководство по программированию: Пер. с англ. - М.: Радио и связь, 1994. 7. Перминов О.Н. Язык программирования Паскаль. - М.: Радио и связь, 1988. - 220 с. 8. Першиков В.И., Савинков В.М. Толковый словарь по информатике. - М.: Финансы и статистика, 1995. |
