лаба элис. Методы выборочных исследований
 Скачать 188.91 Kb. Скачать 188.91 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Южно-Уральский государственный университет (национальный исследовательский университет)» Институт естественных и точных наук Кафедра «Математическое и компьютерное моделирование» Обработка и обобщение на генеральную совокупность результатов простого случайного отбора Отчёт по лабораторной работе №1 по дисциплине «Методы выборочных исследований» Выполнил: Студент группы ЕТ-414 Новикова Алиса Алексеевна ___________ (подпись, дата) Проверил доцент кафедры математического и компьютерного моделирования Акимова Алёна Андреевна ________________________ (оценка, подпись, дата) Даны результаты 11%-го выборочного наблюдения, проведенного методом простого случайного отбора. Дана выборка: 9217; 9165; 9155; 9160; 9367; 9143; 9045; 9149; 9148; 9150; 9077; 9078; 9101; 9100; 9061; 9035; 9324; 9046; 9036; 9037; 9055; 9325; 9258; 9280; 9218; 9050; 9056; 9234; 9137; 9158. 1. Определить 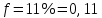 – доля отбора – доля отбора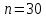 – объем выборки – объем выборки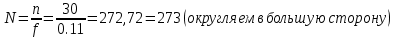 – объем генеральной совокупности – объем генеральной совокупности2. Провести статистическую группировку имеющихся данных выборочного наблюдения двумя независимыми способами. 2.1. Выделить равные интервалы группировки. Ранжированный ряд: 9035; 9036; 9037; 9045; 9046; 9050; 9055; 9056; 9061; 9077; 9078; 9100; 9101;9137; 9143; 9148; 9149; 9150; 9155; 9158; 9160; 9165; 9217; 9218; 9234; 9258 ; 9280; 9324; 9325; 9367 xmin = 9035; xmax = 9367 – наименьшее и наибольшее значения дискретной варианты количественного признака X. h = 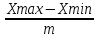 = = 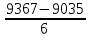 = 53,333 – длина, = 53,333 – длина, где m = 1+3,322∙lg(n) – число интервалов группировки Равные интервалы группировки: [9035; 9090,33] (9090,33; 9145,667] (9145,667; 9201] (9201; 9256,333] (9256,33; 9311,667] (9311,667; 9367] 2.2. Выделить неравные интервалы группировки, величины которых определить по закону, который, на Ваш взгляд, наиболее подходит для обрабатываемой выборки: арифметической прогрессии, геометрической прогрессии, равнонаполненности. Величины определены по закону равнонаполненности интервалов, каждый из которых имеет объем: h =  = = 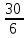 = 5 – длина, где m = 1+3,322∙lg(n) – число интервалов группировки. Неравные интервалы группировки: = 5 – длина, где m = 1+3,322∙lg(n) – число интервалов группировки. Неравные интервалы группировки:
3. Составить таблицу вариационного ряда распределения. Таблица №1 – Дискретный ряд для равных интервалов группировки
где S – накопленная частота, ni – частота,  i – относительная частота, i – относительная частота,hi – высота. Таблица №2 – Дискретный ряд для неравных интервалов группировки
4. Построить гистограмму и кумуляту частот или долей. а) Равные интервалы группировки: 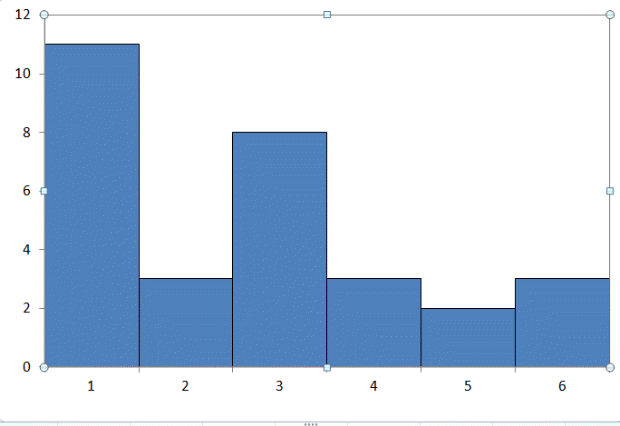 Рис.1.Гистограмма частот для равных интервалов группировки 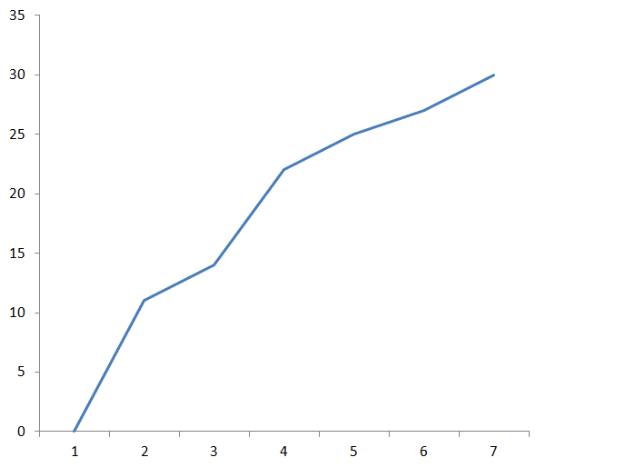 Рис.2.Кумулята частот для равных интервалов группировки б) Неравные интервалы группировки:  Рис. 3 — Гистограмма частот для неравных интервалов группировки 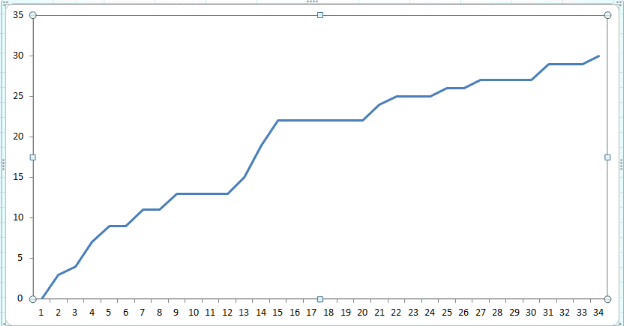 Рис. 4 — Кумулята относительных частот для неравных интервалов группировки 5. Используя результаты группировки, наиболее подходящей для обрабатываемой выборки, определить следующие статистические показатели. Для каждой из четырех характеристик генеральной совокупности: 1) Среднее значение; 2) Суммарное значение; 3)Доля единиц, обладающих значением признака, превышающим предлагаемую оценку среднего значения более чем наmax ([ 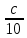 ], { ], { 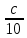 }) %; }) %;4) Число единиц, обладающих значением признака, превышающим предлагаемую оценку среднего значения более чем на max ([ 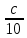 ], { ], { 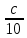 }) % определить: }) % определить:1) выборочное значение; 2) оценку генерального значения; 3) среднюю ошибку выборки; 4) предельную ошибку выборки и границы, в которых находится генеральное значение, с вероятностью 0, 954; 5) относительную предельную ошибку выборки, 6) коэффициент вариации, по которому сделать вывод о пригодности результатов проведенного исследования. max ([ 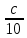 ], { ], { 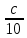 }) % = max ([ }) % = max ([ 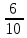 ], { ], { 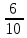 }) % = max ([ }) % = max ([ 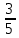 ], { ], { 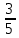 }) % = [0], { 6} % }) % = [0], { 6} %1. Выборочное значение: Для среднего значения:  = = 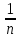 ∙ ∑ ∙ ∑ = = 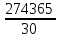 = 9145,5 = 9145,5Для суммарного значения:  = 274365 = 274365Для доли:  x= x=  = =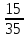 =0, 42, =0, 42,где  число значений в выборке, которые больше 6% от 9145,5 + 9145,5= 548,73 + 9145,5 = 9694,23 число значений в выборке, которые больше 6% от 9145,5 + 9145,5= 548,73 + 9145,5 = 9694,23Чисел, удовлетворяющих такому условию, 15 Для числа единиц генеральной совокупности: 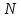 x*= x*=  2. Оценка генерального значения: Для суммарного значения: 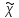 *= ∑ *= ∑ i= i= 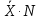 =9145,5 =9145,5  500 = 4572750 500 = 4572750Замечание: 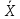 *совпадает с *совпадает с  Для среднего значения: 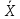 * = * = = 9145,5 = 9145,5Для доли: W*X =  x= 0, 42 x= 0, 42Для числа единиц генеральной совокупности: NX=  x x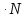 = 0, 42 = 0, 42  195 = 195 = 82 823. Средняя ошибка выборки: а) Бесповторный простой отбор: Для доли: 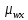 = = 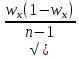 ∙ (1- ∙ (1-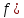 ) = ) =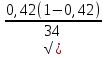 ∙(1- ∙(1-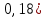 )=0, 07661 )=0, 07661Для среднего значения:  = = 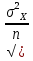 ∙ (1- ∙ (1-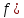 ) = ) =  ∙(1- ∙(1-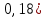 )=36, 92435, )=36, 92435,где 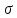 x= ∑ x= ∑  = ∑ = ∑ 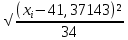 = = 58194, 2333 = 241, 23480– среднее квадратическое отклонение 58194, 2333 = 241, 23480– среднее квадратическое отклонениеДля суммарного значения: 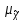 = =  ∙ ∙ 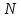 = 36, 92435∙ 195 = 7200, 2385 = 36, 92435∙ 195 = 7200, 2385Для числа единиц генеральной совокупности:  = = 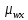 ∙ ∙ 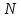 = 0, 07661 ∙ 195 = 14, 93895 = 0, 07661 ∙ 195 = 14, 93895б) Повторный простой отбор: Для доли:  = = 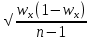 = = 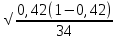 = 0, 08464 = 0, 08464Для среднего значения:  = = 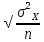 = = 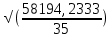 =40, 77612 =40, 77612Для суммарного значения: 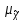 = =  ∙ ∙ 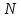 = 40, 77612∙ 195 = 7951, 3434 = 40, 77612∙ 195 = 7951, 3434Для числа единиц генеральной совокупности:  = = 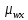 ∙ ∙ 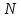 = 0, 08464 ∙ 195 = 15, 5048 = 0, 08464 ∙ 195 = 15, 5048Вывод: целесообразнее применять бесповторный простой отбор, так как средняя ошибка выборки в таком отборе меньше. 4. Предельная ошибка выборки и границы, в которых находится генеральное значение, с вероятностью 0, 954: а) Бесповторный простой отбор: Для доли:  ∙tγ = 0, 07661 ∙ 1, 96= 0, 15015, ∙tγ = 0, 07661 ∙ 1, 96= 0, 15015,где γ = 0, 8-0, 01∙c= 0, 8-0, 01∙0, 18 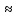 0, 954 – доверительная вероятность, 0, 954 – доверительная вероятность,tγ = 1, 96 – коэффициент доверия,  – средняя ошибка выборки – средняя ошибка выборкиГраницы:  x - x -  ≤ ≤  x ≤ x ≤ x + x + 0, 42 - 0, 15015 ≤0, 42 ≤0, 42 + 0, 15015 0, 26985≤0, 42 ≤0, 57015 Для среднего значения: 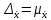 ∙tγ = 36, 92435 ∙1, 96=72, 371726 ∙tγ = 36, 92435 ∙1, 96=72, 371726Границы: 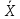 - - 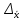 ≤ ≤ 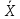 ≤ ≤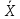 + +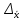 41, 37143 - 72, 371726≤41, 37143≤41, 37143 + 72, 371726 - 31, 000426≤41, 37143≤113, 743156 Для суммарного значения: 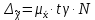 = 36, 92435 ∙ 195∙1, 96=14 112, 48 = 36, 92435 ∙ 195∙1, 96=14 112, 48Границы: 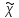 *- *-  ≤ ≤ 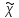 *≤ *≤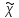 *+ *+ 8067, 42- 14 112, 48 ≤ 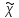 *≤8067, 42+ 14 112, 48 *≤8067, 42+ 14 112, 48-6045, 06 ≤ 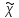 *≤22179, 9 *≤22179, 9Для числа единиц генеральной совокупности:  ∙ ∙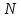 = 0, 07661 ∙ 195∙1, 96=29, 28034 = 0, 07661 ∙ 195∙1, 96=29, 28034Границы: 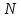 x* - x* -  ≤ ≤ 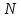 x*≤ x*≤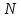 x*+ x*+ 82 - 29, 28034 ≤ 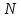 x*≤82 + 29, 28034 x*≤82 + 29, 2803452, 71966≤ 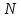 x*≤111, 29034 x*≤111, 29034б) Повторный простой отбор: Для доли:  ∙tγ = 0, 08464∙ 1, 96=0, 16589 ∙tγ = 0, 08464∙ 1, 96=0, 16589Границы:  x - x -  ≤ ≤  x ≤ x ≤ x + x + 0, 42 - 0, 16589≤0, 42 ≤0, 42 + 0, 16589 0, 25411≤0, 42 ≤0, 58589 Для среднего значения: 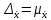 ∙tγ = 40, 77612∙1, 96=79, 92119 ∙tγ = 40, 77612∙1, 96=79, 92119Границы: 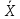 - - 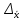 ≤ ≤ 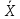 ≤ ≤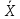 + +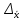 41, 37143 - 79, 92119≤41, 37143≤41, 37143 + 79, 92119 -38, 54976≤41, 37143≤121, 28333 Для суммарного значения: 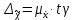 ∙ ∙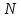 = 40, 77612∙ 195∙1, 96=15 584, 63 = 40, 77612∙ 195∙1, 96=15 584, 63Границы: 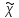 *- *-  ≤ ≤ 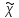 *≤ *≤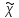 *+ *+ 8067, 42- 15 584, 63 ≤ 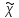 *≤8067, 42+ 15 584, 63 *≤8067, 42+ 15 584, 63-7517, 21≤ 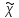 *≤23652, 05 *≤23652, 05Для числа единиц генеральной совокупности:  ∙ ∙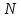 = 0, 08464∙ 195∙1, 96=32, 31996 = 0, 08464∙ 195∙1, 96=32, 31996Границы: 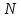 x* - x* -  ≤ ≤ 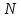 x*≤ x*≤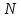 x*+ x*+ 82- 32, 31996 ≤ 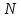 x*≤82 + 32, 31996 x*≤82 + 32, 3199649, 68004≤ 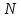 x*≤114, 31996 x*≤114, 319965. Относительная предельная ошибка выборки: а) Бесповторный простой отбор: Для среднего значения: 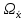 = = 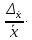 100% = 100% = 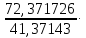 100% = 174, 931% 100% = 174, 931%Для доли: 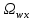 = = 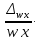 100% = 100% =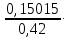 100% =35, 75% 100% =35, 75%Для суммарного значения: 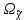 = =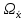 =174, 931% =174, 931%Для числа единиц генеральной совокупности: 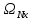 = =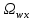 =35, 75% =35, 75%б) Повторный простой отбор: Для среднего значения: 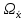 = = 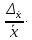 100% = 100% =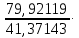 100% = 193, 179% 100% = 193, 179%Для доли: 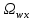 = = 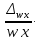 100% = 100% = 100% =39, 497% 100% =39, 497%Для суммарного значения: 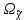 = =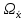 =193, 179% =193, 179%Для числа единиц генеральной совокупности: 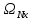 = =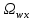 =39, 497% =39, 497%6. Коэффициент вариации, по которому сделать вывод о пригодности результатов проведенного исследования: а) Бесповторный простой отбор: Для среднего значения: 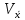 = =  100% = 100% =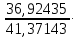 100% = 89,25% 100% = 89,25%Для доли: 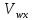 = = 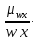 100% = 100% =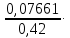 100% =18,24% 100% =18,24%Для суммарного значения: 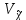 = =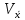 =89,25% =89,25%Для числа единиц генеральной совокупности: 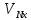 = = 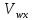 =18,24% =18,24%б) Повторный простой отбор: Для среднего значения: 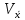 = =  100% = 100% =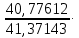 100% = 98,56% 100% = 98,56%Для доли: 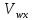 = = 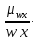 100% = 100% = 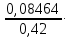 100% =20,15% 100% =20,15%Для суммарного значения:  = = =98,56% =98,56%Для числа единиц генеральной совокупности:  = = 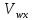 =20,15% =20,15%Вывод: так как коэффициент вариации более 5%, результаты выборочного исследования следует рассматривать как мало пригодные. Использованные обозначения: *- оценка 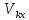 – коэффициент вариации – коэффициент вариации – относительная предельная ошибка – относительная предельная ошибкаЧелябинск, 2022 г. |
