|
Методичка МОИБ.. Методические разработки к лабораторным работам по дисциплине средства обеспечения информационной безопасности в сетях передачи данных для студентов специальностей 200900, 201000, 201800
Л
53
абораторная работа №4
ИЗУЧЕНИЕ АЛГОРИТМА ДИФФИ-ХЕЛЛМАНА ОТКРЫТОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ
1. Цель работы
Изучить основные принципы и процедурные аспекты алгоритма Диффи-Хеллмана открытого распределения ключей.
2. Рекомендуемые источники
1.Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина.- 2-е изд.. перераб. и доп..-М.: Радио и связь, 2001, с. 182-199.
2.Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах.- М.: ДМК Пресс, 2002, с. 269-286.
3.Б.Шнайер. Прикладная криптография.-М.: Триумф, 2002, с. 573-576.
3. Подготовка к работе
Ознакомиться с алгоритмом открытого распределения ключей по одному из рекомендованных источников/1-3/.
Ознакомиться с содержанием данной методической разработки.
Подготовить бланк отчета, который должен содержать:
- цель работы;
- основные математические соотношения для обоснования алгоритма.
- заготовку таблицы, в которую будет заноситься ключевая информация в процессе изучения алгоритма.
54
4. Контрольные вопросы
Сущность процедуры управления криптографическими ключами.
Назначение и особенности генерации ключей.
Назначение и особенности хранения ключей.
Концепция иерархии ключей.
Назначение и особенности распределения ключей.
Централизованное распределение ключей.
Протокол аутентификации и распределения ключей для симметричных криптосистем.
Протокол для асимметричных криптосистем с использованием сертификатов открытых ключей.
Алгоритм открытого распределения ключей Диффи-Хеллмана.
Схема реализации алгоритма Диффи-Хеллмана.
Приведите математическое доказательство возможности формирования у абонентов двух одинаковых ключей без передачи секретной информации.
5. Содержание работы
Ознакомиться с постановкой задачи управления криптографическими ключами.
Ознакомиться с математическими соотношениями, лежащими в основе алгоритма Диффи-Хеллмана.
Изучить основные этапы алгоритма.
Произвести установку открытых и закрытых ключей двух абонентов.
Наблюдать поведение алгоритма при изменении соответствующих параметров.
6. Содержание отчета
Ц
55
ель работы.
Структурная схема алгоритма распределения ключей Диффи-Хеллмана.
Основные математические соотношения, предписываемые алгоритмом Диффи-Хеллмана.
Привести значения предварительно устанавливаемых параметров и значения, устанавливаемые и возникающие в процессе каждого сеанса.
7. Методические указания к выполнению работы
Для реализации любой одноключевой криптосистемы необходим обмен секретными ключами шифрования. Передача таких ключей по открытым каналам не имеет смысла, так как может стать легкой добычей злоумышленника. Передавать ключи по закрытым каналам тоже опасно, так как в этом случае однократная компрометация канала рассекречивает весь дальнейший обмен. Поэтому единственным надежным средством доставки ключевой информации для особо важного обмена до недавнего времени считалась фельдъегерская почта. В современных условиях, например, для миллионов пользователей Internet такая система неприемлема.
В 1976 году Диффи и Хеллман /1,2,3/ опубликовали алгоритм открытого распределения ключей, который позволяет двум абонентам путем обмена открытыми сообщениями сформировать одинаковые секретные ключи для своей одноключевой (симметричной) системы шифрования.
В основе метода лежит свойство односторонней функции y=f(x), в которой, зная х сравнительно легко вычислить y, но вычисление х при известном у выливается в задачу, сопоставимую с полным перебором.
С
56
уть алгоритма Диффи-Хеллмана состоит в следующем.
Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.
1. Обе стороны заранее уславливаются о модуле n (n должно быть простым числом) и примитивном элементе с (1<c < n). Эти два целых числа n и с могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.
2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи Хa и Хb (Хa и Хb – случайные большие целые числа, которые хранятся пользователями А и В в секрете).
3. Далее пользователь А вычисляет открытый ключ Ya= (cXa)mod n,
а пользователь В – открытый ключ Yb = (cXb) mod n.
4. Затем стороны обмениваются вычисленными значениями открытых ключей Ya и Yb по любому, даже совсем незащищенному каналу, т.к. открытые ключи не являются секретом. (Мы считаем, что все данные, передаваемые по незащищенному каналу связи, могут быть перехвачены злоумышленником).
5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие соотношения:
пользователь А: Kab= (YbXa)mod n = (cXbXa)mod n,
пользователь В: Kba= (YaXb)mod n = (cXaXb)mod n.
Очевидно, что Kab= Kba.
Ключ К может использоваться в качестве общего секретного ключа (ключа шифрования), например, в таких симметричных криптосистемах, как DES, ГОСТ 28147-89, AES и др.
Возможные действия злоумышленника.
П
57
ерехватив значения n, c, Ya и Yb, криптоаналитик тоже хотел бы определить значения ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения Хa по n, c и Ya, что ( cXa)mod n = Ya (поскольку в этом случае, вычислив Xa, можно найти K = (YbXa)mod n). Однако нахождение Xa по n, c и Ya – это задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.
Выбор значений n и c может иметь существенное влияние на безопасность этой системы. Модуль n должен быть большим и простым числом. Число (n-1)/2 также должно быть простым числом. Число с желательно выбирать таким, чтобы оно было примитивным элементом множества ненулевых элементов Zn, т.е. {c,c2,….cn-1} = Zn – {0}.
В принципе достаточно, чтобы с генерировало большую подгруппу мультипликативной группы по mod n.
Алгоритм открытого распределения ключей Диффи-Хеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.
Метод Диффи-Хеллмана дает возможность шифровать данные при каждом сеансе связи на новых ключах. Это позволяет не хранить секреты на дискетах или других носителях. Не следует забывать, что любое хранение секретов повышает вероятность попадания их в руки конкурентов или противника.
П
58
реимущество метода Диффи-Хеллмана по сравнению с методом RSA заключается в том, что формирование общего секретного ключа происходит в сотни раз быстрее. В системе RSA генерация новых секретных и открытых ключей основана на генерации новых простых чисел, что занимает много времени. Кроме того, сам процесс зашифровывания и расшифровывания информации в симметричных (одноключевых) системах протекает значительно быстрее, чем в асимметричных (двухключевых), а система Диффи-Хеллмана как раз и ориентирована на то, что сам процесс информационного обмена будет производиться в симметричных системах.
8. Лабораторное задание
1.Произвести рапределение ключей при различных значениях аргументов n, c, Xa и Xb.
2.Зафиксировать по секундомеру длительность выполнения основных процедур при различной длительности аргументов.
3.Выход на рабочее поле алгоритма производится из Главного меню вызовом пункта «Диффи-Хеллман».
4.Установку открытых ключей n и с произвести с учетом указанных ограничений. Вышеупомянутые требования к значениям n и c (n –простое, а с - примитивный элемент поля GF(n)) не являются строго обязательными.
5.Понаблюдайте за поведением системы при значениях c=1 и c=n-1. Объясните результаты.
9. Общие сведения
9.1. Управление криптографическими ключами
Л
59
юбая криптографическая система основана на использовании криптографических ключей. В симметричной криптосистеме отправитель и получатель сообщения используют один и тот же секретный ключ. Этот ключ должен быть неизвестен всем остальным и должен периодически обновляться одновременно у отправителя и получателя. Процесс распределения (рассылки) секретных ключей между участниками информационного обмена в симметричных криптосистемах имеет весьма сложный характер.
Асимметричная криптосистема предполагает использование двух ключей – открытого и личного (секретного). Открытый ключ можно разглашать, а личный надо хранить в тайне. При обмене сообщениями необходимо пересылать только открытый ключ. Важным требованием является обеспечение подлинности отправителя сообщения. Это достигается путем взаимной аутентификации участников информационного обмена.
Под ключевой информацией понимают совокупность всех действующих в сети ключей. Если не обеспечено достаточно надежное управление ключевой информацией, то, завладев ею, злоумышленник получает неограниченный доступ ко всей информации.
Управление ключами – информационный процесс, включающий реализацию следующих основных функций:
- генерация ключей;
- хранение ключей;
- распределение ключей.
9.1.1. Генерация ключей
Безопасность любого криптографического алгоритма определяется используемым криптографическим ключом. Добротные криптографические ключи должны иметь достаточную длину и случайные значения битов.
Для получения ключей используются аппаратные и программные средства генерации случайных значений ключей. Как правило, применяют датчики псевдослучайных чисел (ПСЧ). Однако степень случайности генерации чисел должна быть достаточно высокой. Идеальными генераторами являются устройства на основе "натуральных" случайных процессов, например на основе белого радиошума.
В
60
сети со средними требованиями защищенности вполне приемлемы программные генераторы ключей, которые вычисляют ПСЧ как сложную функцию от текущего времени и (или) числа, введенного пользователем.
Один из методов генерации сеансового ключа для симметричных криптосистем описан в стандарте ANSI X9.17. Он предполагает использование криптографического алгоритма DES (хотя можно применить и другие симметричные алгоритмы шифрования).
Обозначения:
ЕК (X) – результат шифрования алгоритмом DES значения X;
К – ключ, зарезервированный для генерации секретных ключей;
V0 – секретное 64-битовое начальное число;
Т – временная отметка.
Схема генерации случайного сеансового ключа Ri в соответствии со стандартом ANSI X 9.17 показана на рис.4.1. Случайный ключ Ri генерируют, вычисляя значение
Ri = ЕК (ЕК (Тi) Å Vi).
Р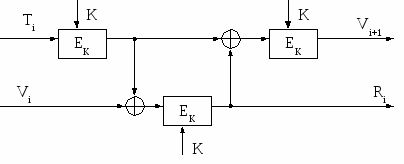
61
исунок4. 1- Схема генерации случайного ключа Ri в соответствии со стандартом ANSI X9.17
Следующее значение Vi+1 вычисляют так:
Vi+1 = ЕК (ЕК (Тi) Å Ri).
Если необходим 128-битовый случайный ключ, генерируют пару ключей Ri, Ri+1 и объединяют их вместе.
Если ключ не меняется регулярно, это может привести к его раскрытию и утечке информации. Регулярную замену ключа можно осуществить, используя процедуру модификации ключа.
Модификация ключа – это генерирование нового ключа из предыдущего значения ключа с помощью односторонней (однонаправленной) функции. Участники информационного обмена разделяют один и тот же ключ и одновременно вводят его значение в качестве аргумента в одностороннюю функцию, получая один и тот же результат. Затем они берут определенные биты из этих результатов, чтобы создать новое значение ключа.
Процедура модификации ключа работоспособна, но надо помнить, что новый ключ безопасен в той же мере, в какой был безопасен прежний ключ. Если злоумышленник сможет добыть прежний ключ, то он сможет выполнить процедуру модификации ключа.
Генерация ключей для асимметричных криптосистем с открытыми ключами много сложнее, потому что эти ключи должны обладать определенными математическими свойствами (они должны быть очень большими и простыми и т.д.).
9.1.2. Хранение ключей
П
62
од функцией хранения ключей понимают организацию их безопасного хранения, учета и удаления. Ключ является самым привлекательным для злоумышленника объектом, открывающим ему путь к конфиденциальной информации. Поэтому вопросам безопасного хранения ключей следует уделять особое внимание. Секретные ключи никогда не должны записываться в явном виде на носителе, который может быть считан или скопирован.
Носители ключевой информации.
Ключевой носитель может быть технически реализован различным образом на разных носителях информации - магнитных дисках, устройствах хранения ключей типа TOUCH MEMORY, пластиковых картах и т.д..
Магнитные диски представляют собой распространенный тип носителя ключевой информации. Применение магнитного диска (МД) в качестве носителя ключа позволяет реализовать необходимое свойство отчуждаемости носителя ключа от защищенной компьютерной системы, т.е. осуществлять временное изъятие МД из состава технических средств компьютерной системы. Особенно целесообразно использование в качестве ключевых носителей съемных накопителей – гибких магнитных дисков, съемных магнитооптических носителей и т.д..
Основное преимущество МД по сравнению с другими носителями ключевой информации заключается в том, что оборудование для взаимодействия с МД (дисковод) входит в состав штатных средств компьютера.
Другая важная особенность, определяющая широкое распространение МД, - стандартный формат хранения информации на дисках и стандартные программные средства доступа к дискам. Кроме того, из всех средств хранения ключевой информации гибкие магнитные диски имеют самую низкую стоимость..
Д
63
ля обеспечения надежного хранения ключевой информации на МД применяют как минимум двукратное резервирование объектов хранения. Это позволяет защитить ключевую информацию от ошибок при считывании с МД и от сбоев программной и аппаратной части.
Для предотвращения возможности перехвата ключевой информации в процессе ее чтения с МД применяют хранение ключевой информации на МД в зашифрованном виде.
Устройство хранения ключей типа TOUCH MEMORY является относительно новым носителем ключевой информации, предложенным американской компанией Dallas Semiconductor. Носитель информации TOUCH MEMORY (ТМ) представляет собой энергонезависимую память, размещенную в металлическом корпусе, с одним сигнальным контактом и одним контактом земли. Корпус ТМ имеет диаметр 16,25 мм и толщину 3,1 или 5,89 мм (в зависимости от модификации прибора).
В структуру ТМ входят следующие основные блоки.
Постоянное запоминающее устройство (ПЗУ) хранит 64-разрядный код, состоящий из байтового кода типа прибора, 48-битового уникального серийного номера и 8-битовой контрольной суммы. Содержимое ПЗУ уникально и не может быть изменено в течение всего срока службы прибора.
Оперативное запоминающее устройство (ОЗУ) емкостью от 128 до 8192 байт содержат практически все модификации ТМ. В одной из модификаций оперативная память аппаратно защищена от несанкционированного доступа.
Встроенная миниатюрная литиевая батарейка со сроком службы не менее 10 лет обеспечивает питанием все блоки устройства.
О
64
собенностью технологии хранения и обмена ключевой информации между носителем ТМ и внешними устройствами является сравнительно низкая скорость (обусловленная последовательной передачей данных) и высокая вероятность сбоя в тракте чтения-записи, обусловленная тем, что контакт устройства ТМ с устройством чтения осуществляется пользователем вручную без дополнительной фиксации (простое касание, что и определило название прибора ТМ). В связи с этим особое значение приобретают вопросы надежного обмена между программами обработки ключевой информации пользователей и носителем ТМ.
В устройстве ТМ конструктивно отработаны вопросы надежности функционирования и вопросы интерфейса со считывающим устройством на основе одного сигнального контакта. Для обеспечения достоверного чтения применяются корректирующие коды, для обеспечения достоверной записи в приборе предусмотрена технология буферизации. При проведении операции записи первоначально вектор передаваемой в ТМ информации помещается в буфер, далее выполняется операция чтения из буфера, затем прочтенная из буфера информация сравнивается с записываемой и в случае совпадения подается сигнал на перенос информации из буфера в память долговременного хранения.
Таким образом, носитель ТМ является микроконтроллерным устройством без собственной вычислительной мощности и с ограниченным объемом хранения, но с достаточно высокими надежностными характеристиками. Поэтому применение ТМ вполне обосновано в случае повышенных требований к надежности носителя ключа и небольшого объема ключевой информации, хранимой в ТМ.
Э
65
лектронные пластиковые карты становятся в настоящее время наиболее распространенным и универсальным носителем конфиденциальной информации, который позволяет идентифицировать и аутентифицировать пользователей, хранить криптографические ключи, пароли и коды.
Интеллектуальные карты (смарт-карты), обладающие наибольшими возможностями, эффективно применяются не только для хранения ключевой информации, но и широко используются в электронных платежных системах, в комплексных решениях для медицины, транспорта, связи, образования и т.п. Более подробные сведения об электронных пластиковых картах приводятся в разделе 9.4.
9.1.3. Концепция иерархии ключей.
Любая информация об используемых ключах должна быть защищена, в частности храниться в зашифрованном виде.
Необходимость в хранении и передаче ключей, зашифрованных с помощью других ключей, приводит к концепции иерархии ключей. В стандарте ISO 8532 (Banking-Key Management) подробно изложен метод главных/сеансовых ключей (master/session keys). Суть метода состоит в том, что вводится иерархия ключей: главный ключ (ГК), ключ шифрования ключей (КК), ключ шифрования данных (КД).
Иерархия ключей может быть:
- двухуровневой (КК/КД),
- трехуровневой (ГК/КК/КД).
С
66
амым нижним уровнем являются рабочие или сеансовыe КД, которые используются для шифрования данных, персональных идентификационных номеров (PIN) и аутентификации сообщений. Когда эти ключи надо зашифровать с целью защиты при передаче или хранении, используют ключи следующего уровня – ключи шифрования ключей. Ключи шифрования ключей никогда не должны использоваться как сеансовые (рабочие) КД, и наоборот.
Такое разделение функций необходимо для обеспечения максимальной безопасности. Фактически стандарт устанавливает, что различные типы рабочих ключей (например, для шифрования данных, для аутентификации и т.д.) должны всегда шифроваться с помощью различных версий ключей шифрования ключей.
В частности, ключи шифрования ключей, используемые для пересылки ключей между двумя узлами сети, известны также как ключи обмена между узлами сети (cross domain keys). Обычно в канале используются два ключа для обмена между узлами сети, по одному в каждом направлении. Поэтому каждый узел сети будет иметь ключ отправлениядля обмена с узлами сети и ключ получения для каждого канала, поддерживаемого другим узлом сети.
На верхнем уровне иерархии ключей располагается главный ключ, мастер-ключ. Этот ключ применяют для шифрования КК, когда требуется сохранить их на диске. Обычно в каждом компьютере используется только один мастер-ключ.
Мастер-ключ распространяется между участниками обмена неэлектронным способом – при личном контакте, чтобы исключить его перехват и/или компрометацию. Раскрытие противником значения мастер-ключа полностью уничтожает защиту компьютера.
З
67
начение мастер-ключа фиксируется на длительное время (до нескольких недель или месяцев). Поэтому генерация и хранение мастер-ключей являются критическими вопросами криптографической защиты. На практике мастер-ключ компьютера создается истинно случайным выбором из всех возможных значений ключей. Мастер-ключ помещают в защищенный по считыванию и записи и от механических воздействий блок криптографической системы таким образом, чтобы раскрыть значение этого ключа было невозможно. Однако все же должен существовать способ проверки, является ли значение ключа правильным.
Проблема аутентификации мастер-ключа может быть решена различными путями. Один из способов аутентификации показан на рис. 4.2 .
Р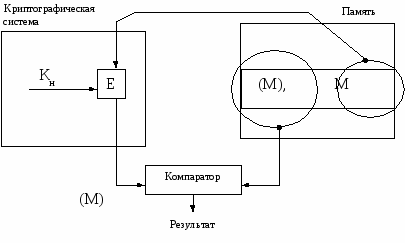
исунок 4.2- Схема аутентификации мастер-ключа хост-компьютера
А
68
дминистратор, получив новое значение мастер-ключа КН хост-компьютера, шифрует некоторое сообщение М ключом КН. Пара (криптограмма ЕкН (М), сообщение М) помещается в память компьютера. Всякий раз, когда требуется аутентификация мастер-ключа хост-компьютера, берется сообщение М из памяти и подается в криптографическую систему. Получаемая криптограмма сравнивается с криптограммой, хранящейся в памяти. Если они совпадают, считается, что данный ключ является правильным.
Рабочие ключи (например, сеансовый) обычно создаются с помощью псевдослучайного генератора и могут храниться в незащищенном месте. Это возможно, поскольку такие ключи генерируются в форме соответствующих криптограмм, т.е. генератор ПСЧ выдает вместо ключа КS его криптограмму 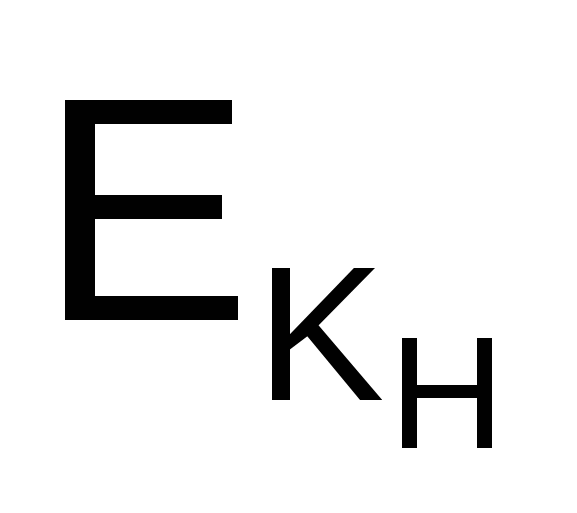 (КS), получаемую с помощью мастер-ключа хост-компьютера. Расшифровывание такой криптограммы выполняется только перед использованием ключа КS. (КS), получаемую с помощью мастер-ключа хост-компьютера. Расшифровывание такой криптограммы выполняется только перед использованием ключа КS.
Схема защиты рабочего (сеансового) ключа показана на рис. 4.3. Чтобы зашифровать сообщение М ключом КS, на соответствующие входы криптографической системы подается криптограмма 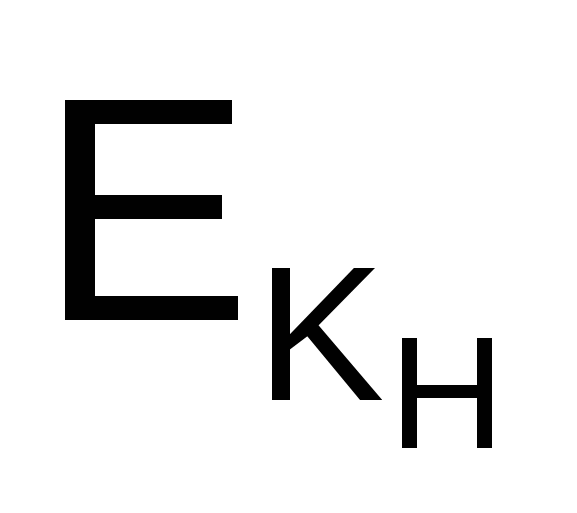 (КS) и сообщение М. Криптографическая система сначала восстанавливает ключ КS, а затем шифрует сообщение М, используя открытую форму сеансового ключа КS. (КS) и сообщение М. Криптографическая система сначала восстанавливает ключ КS, а затем шифрует сообщение М, используя открытую форму сеансового ключа КS.
Р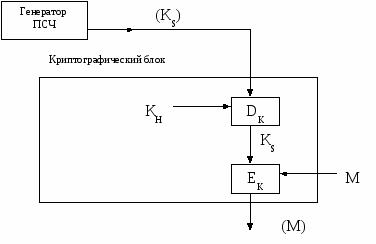
69
исунок4.3- Схема защиты сеансового ключа КS
Таким образом, безопасность сеансовых ключей зависит от безопасности криптографической системы. Криптографический блок может быть спроектирован как единая СБИС и помещен в физически защищенное место.
Очень важным условием безопасности информации является периодическое обновление ключевой информации. При этом должны переназначаться как рабочие ключи, так и мастер-ключи. В особо ответственных сетях обновление ключевой информации (сеансовых ключей) желательно делать ежедневно. Вопрос обновления ключевой информации тесно связан с третьим элементом управления ключами – распределением ключей.
9.1.4. Распределение ключей
Распределение ключей – самый ответственный процесс в управлении ключами. К нему предъявляются следующие требования:
- оперативность и точность распределения;
- скрытность распределяемых ключей.
Распределение ключей между пользователями компьютерной сети реализуется двумя способами:
1) использованием одного или нескольких центров распределения ключей;
2) прямым обменом сеансовыми ключами между пользователями сети.
Н
70
едостаток первого подхода состоит в том, что центру распределения ключей известно, кому и какие ключи распределены, и это позволяет читать все сообщения, передаваемые по сети. Возможные злоупотребления существенно влияют на защиту. При втором подходе проблема состоит в том, чтобы надежно удостоверить подлинность субъектов сети.
В обоих случаях должна быть обеспечена подлинность сеанса связи. Это можно осуществить, используя механизм запроса-ответа или механизм отметки времени.
Механизм запроса-ответа заключается в следующем. Пользователь А включает в посылаемое сообщение (запрос) для пользователя В непредсказуемый элемент (например, случайное число). При ответе пользователь В должен выполнить некоторую операцию с этим элементом (например, добавить единицу), что невозможно осуществить заранее, поскольку неизвестно, какое случайное число придет в запросе. После получения результата действий пользователя В (ответ) пользователь А может быть уверен, что сеанс является подлинным.
Механизм отметки времени предполагает фиксацию времени для каждого сообщения. Это позволяет каждому субъекту сети определить, насколько старо пришедшее сообщение, и отвергнуть его, если появится сомнение в его подлинности. При использовании отметок времени необходимо установить допустимый временной интервал задержки.
В обоих случаях для защиты элемента контроля используют шифрование, чтобы быть уверенным, что ответ отправлен не злоумышленником и не изменен штемпель отметки времени.
Задача распределения ключей сводится к построению протокола распределения ключей, обеспечивающего:
- взаимное подтверждение подлинности участников сеанса;
- подтверждение достоверности сеанса механизмом запроса-ответа или отметки времени;
- использование минимального числа сообщений при обмене ключами;
-
71
возможность исключения злоупотреблений со стороны центра распределения ключей (вплоть до отказа от него).
В основу решения задачи распределения ключей целесообразно положить принцип отделения процедуры подтверждения подлинности партнеров от процедуры собственно распределения ключей. Цель такого подхода состоит в создании метода, при котором после установления подлинности участники сами формируют сеансовый ключ без участия центра распределения ключей с тем, чтобы распределитель ключей не имел возможности выявить содержание сообщений.
9.1.5. Распределение ключей с участием центра
распределения ключей
При распределении ключей между участниками предстоящего информационного обмена должна быть гарантирована подлинность сеанса связи. Для взаимной проверки подлинности партнеров приемлема модель рукопожатия. В этом случае ни один из участников не будет получать никакой секретной информации во время процедуры установления подлинности.
Взаимное установление подлинности гарантирует вызов нужного субъекта с высокой степенью уверенности, что связь установлена с требуемым адресатом и никаких попыток подмены не было. Реальная процедура организации соединения между участниками информационного обмена включает как этап распределения, так и этап подтверждения подлинности партнеров.
П
72
ри включении в процесс распределения ключей центра распределения ключей (ЦРК) осуществляется его взаимодействие с одним или обоими участниками сеанса с целью распределения секретных или открытых ключей, предназначенных для использования в последующих сеансах связи.
Следующий этап – подтверждение подлинности участников – содержит обмен удостоверяющими сообщениями, чтобы иметь возможность выявить любую подмену или повтор одного из предыдущих вызовов.
Рассмотрим протоколы для симметричных криптосистем с секретными ключами и для асимметричных криптосистем с открытыми ключами. Вызывающий (исходный объект) обозначается через А, а вызываемый (объект назначения) – через В. Участники сеанса А и В имеют уникальные идентификаторы IdA и IdB соответственно.
9.1.6. Протокол аутентификации и распределения
ключей для симметричных криптосистем
Рассмотрим в качестве примера протокол аутентификации и распределения ключей Kerberos (по-русски – Цербер). Первоначально протокол Kerberos был разработан в Массачусетском Технологическом Институте (США) для проекта Athena. Протокол Kerberos спроектирован для работы в сетях TCP/IP и предполагает участие в аутентификации и распределении ключей третьей доверенной стороны. Kerberos обеспечивает надежную аутентификацию в сети, разрешая законному пользователю доступ к различным машинам в сети. Протокол Kerberos основывается на симметричной криптографии (реализован алгоритм DES, хотя возможно применение и других симметричных криптоалгоритмов). Kerberos разделяет отдельный секретный ключ с каждым субъектом сети, и знание такого секретного ключа равносильно доказательству подлинности субъекта сети.
О
73
сновной протокол Kerberos является вариантом протокола аутентификации и распределения ключей Нидхема-Шредера. В основном протоколе Kerberos (версия 5) участвуют две взаимодействующие стороны А и В и доверенный сервер KS (Kerberos Server). Стороны А и В, каждая по отдельности, разделяют свой секретный ключ с сервером KS. Доверенный сервер KS выполняет роль центра распределения ключей ЦРК.
Пусть сторона А хочет получить сеансовый ключ для информационного обмена со стороной В.
Сторона А инициирует фазу распределения ключей, посылая по сети серверу KS идентификаторы IdA и IdB:
(1) A ® KS: IdA, IdB.
Сервер KS генерирует сообщение с временной отметкой Т, сроком действия L, случайным сеансовым ключом К и идентификатором IdA. Он шифрует это сообщение секретным ключом, который разделяет со стороной В.
Затем сервер KS берет временную отметку Т, срок действия L, сеансовый ключ К, идентификатор IdB стороны В и шифрует все это секретным ключом, который разделяет со стороной А. Оба эти зашифрованные сообщения он отправляет стороне А:
(2) KS ® A: EA (T, L, K, IdB), EB (T, L, K, IdA).
Сторона А расшифровывает первое сообщение своим секретным ключом, проверяет отметку времени Т, чтобы убедиться, что это сообщение не является повторением предыдущей процедуры распределения ключей.
Затем сторона А генерирует сообщение со своим идентификатором IdA и отметкой времени Т, шифрует его сеансовым ключом К и отправляет стороне В. Кроме того, А отправляет для В сообщение от KS, зашифрованное ключом стороны В:
(3) A ® B: EK (IdA, T), EB (T, L, K, IdA).
Т
74
олько сторона В может расшифровать сообщения (3). Сторона В получает отметку времени Т, срок действия L, сеансовый ключ К и идентификатор IdA. Затем сторона В расшифровывает сеансовым ключом К вторую часть сообщения (3). Совпадение значений Т и IdA в двух частях сообщения подтверждают подлинность А по отношению к В.
Для взаимного подтверждения подлинности сторона В создает сообщение, состоящее из отметки времени Т плюс 1, шифрует его ключом К и отправляет стороне A:
(4) B ® A: EK (T+1).
Если после расшифрования сообщения (4) сторона А получает ожидаемый результат, она знает, что на другом конце линии связи находится действительно В.
Этот протокол успешно работает при условии, что часы каждого участника синхронизированы с часами сервера KS. Следует отметить, что в этом протоколе необходим обмен с KS для получения сеансового ключа каждый раз, когда А желает установить связь с В. Протокол обеспечивает надежное соединение объектов А и В при условии, что ни один из ключей не скомпрометирован и сервер KS защищен.
Система Kerberos обеспечивает защиту сети от несанкционированного доступа, базируясь исключительно на программных решениях, и предполагает многократное шифрование передаваемой по сети управляющей информации.
Система Kerberos имеет структуру типа клиент-сервер и состоит из клиентских частей С, установленных на все машины сети (рабочие станции пользователей и серверы), и Kerberos-сервера KS, располагающегося на каком-либо (не обязательно выделенном) компьютере.
K
75
erberos-сервер, в свою очередь, можно разделить на две части: сервер идентификации AS (Authentication Server) и сервер выдачи разрешений TGS (Ticket Granting Server). Информационными ресурсами, необходимыми клиентам С, управляет сервер информационных ресурсов RS (рис.4.4).
Область действия системы Kerberos распространяется на тот участок сети, все пользователи которого зарегистрированы под своими именами и паролями в базе данных Kerberos-сервера.
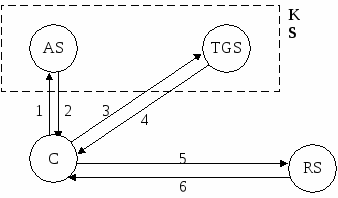
Рисунок 4.4- Схема и шаги протокола Kerberos.
Обозначения:
KS - сервер системы Kerberos;
AS - сервер идентификации;
TGS - сервер выдачи разрешений;
RS - сервер информационных ресурсов;
C - клиент системы Kerberos;
1 : C ® AS : - запрос разрешить обратиться к TGS;
2 : AS ® C : - разрешение обратиться к TGS;
3 : C ® TGS : - запрос на допуск к RS;
4 : TGS ® C : - разрешение на допуск к RS;
5 : C ® RS : - запрос на получение информационного ресурса от RS;
6
76
: RS ® C : - подтверждение подлинности сервера RS и предоставление информационного ресурса.
Укрупненно процесс идентификации и аутентификации пользователя в системе Kerberos можно списать следующим образом. Пользователь (клиент) С, желая получить доступ к ресурсу сети, направляет запрос серверу идентификации AS. Последний идентифицирует пользователя с помощью его имени и пароля и выдает разрешение на доступ к серверу выдачи разрешений TGS, который в свою очередь, по запросу клиента С разрешает использование необходимых ресурсов сети с помощью целевого сервера информационных ресурсов RS.
Данная модель взаимодействия клиента с серверами может функционировать только при условии обеспечения конфиденциальности и целостности передаваемой управляющей информации. Без строгого обеспечения информационной безопасности клиент не может отправлять серверам AS, TGS и RS свои запросы и получать разрешения на доступ к обслуживанию в сети. Чтобы избежать возможности перехвата и несанкционированного использования информации, Kerberos применяет при передаче любой управляющей информации в сети сложную систему многократного шифрования с использованием комплекса секретных ключей (секретный ключ клиента, секретный ключ сервера, секретные сеансовые ключи, клиент-сервер).
9.1.7. Протокол для асимметричных криптосистем
с использованием сертификатов открытых ключей
В этом протоколе используется идея сертификатов открытых ключей.
С
77
ертификатом открытого ключа С называется сообщение ЦРК, удостоверяющее целостность некоторого открытого ключа объекта. Например, сертификат открытого ключа для пользователя А, обозначаемый СА, содержит отметку времени Т, идентификатор IdА и открытый ключ КА, зашифрованные секретным ключом ЦРК kЦРК, т.е.
СА = 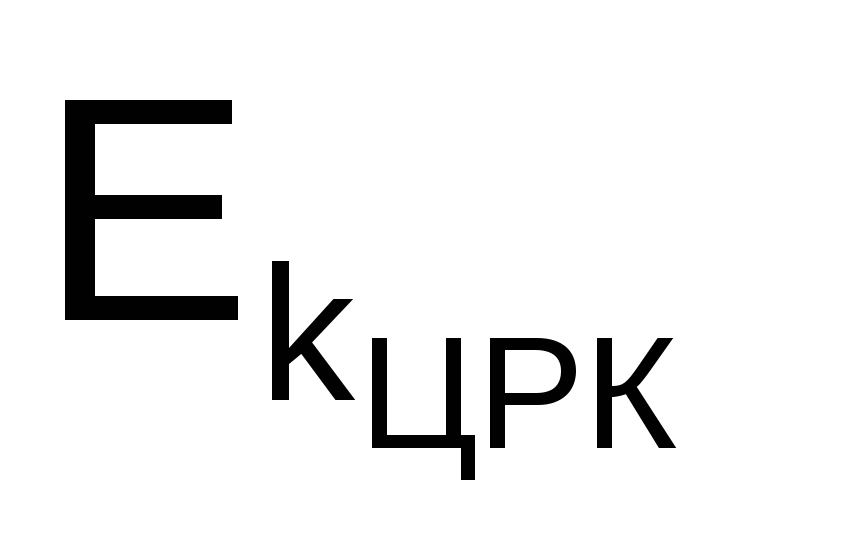 (Т, IdА, КА). (Т, IdА, КА).
Отметка времени Т используется для подтверждения актуальности сертификата и тем самым предотвращает повторы прежних сертификатов, которые содержат открытые ключи и для которых соответствующие секретные ключи несостоятельны.
Секретный ключ kЦРК известен только менеджеру ЦРК. Открытый ключ К ЦРК известен участникам А и В. ЦРК поддерживает таблицу открытых ключей всех объектов сети, которые он обслуживает.
Вызывающий объект А инициирует стадию установления ключа, запрашивая у ЦРК сертификат своего открытого ключа и открытого ключа участника В:
(1) А ® ЦРК : IdA, IdB,
´Вышлите сертификаты ключей А и В´. Здесь IdA и IdB – уникальные идентификаторы соответственно участников А и В.
Менеджер ЦРК отвечает сообщением
(2) ЦРК ® А : 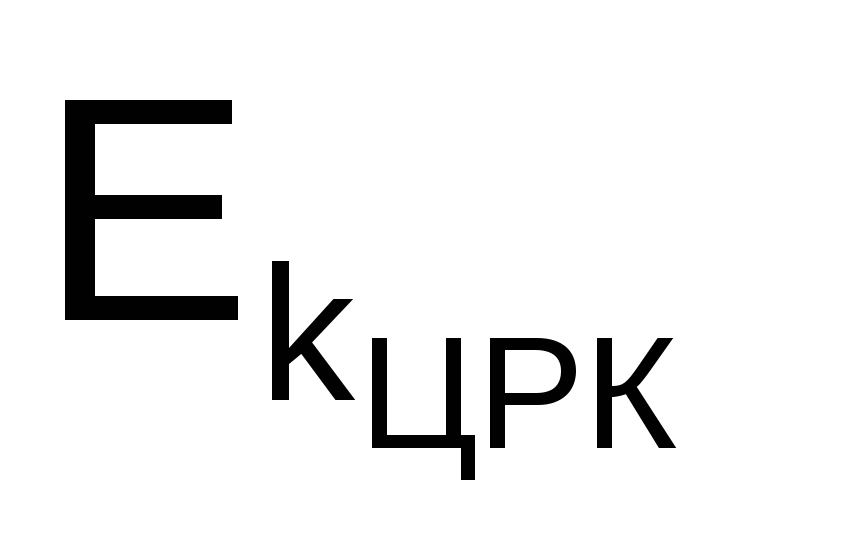 (Т, IdA, КА), (Т, IdA, КА), 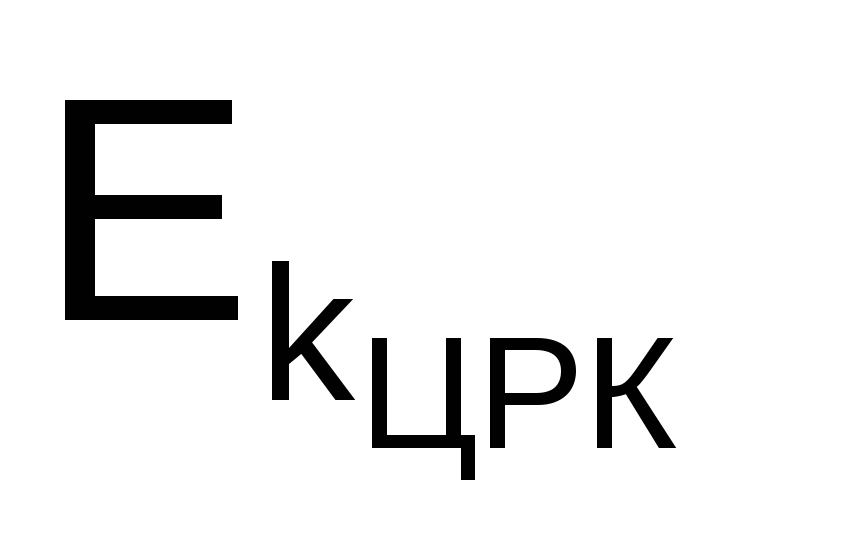 (Т, IdB, КВ). (Т, IdB, КВ).
Участник А, используя открытый ключ ЦРК КЦРК, расшифровывает ответ ЦРК, проверяет оба сертификата. Идентификатор IdB убеждает А, что личность вызываемого участника правильно зафиксирована в ЦРК и КВ – действительно открытый ключ участника В, поскольку оба зашифрованы ключом kЦРК.
Х
78
отя открытые ключи предполагаются известными всем, посредничество ЦРК позволяет подтвердить их целостность. Без такого посредничества злоумышленник может снабдить А своим открытым ключом, который А будет считать ключом участника В. Затем злоумышленник может подменить собой В и установить связь с А, и его никто не сможет выявить.
Следующий шаг протокола включает установление свя-зи А с В:
(3) А ® В : СА, 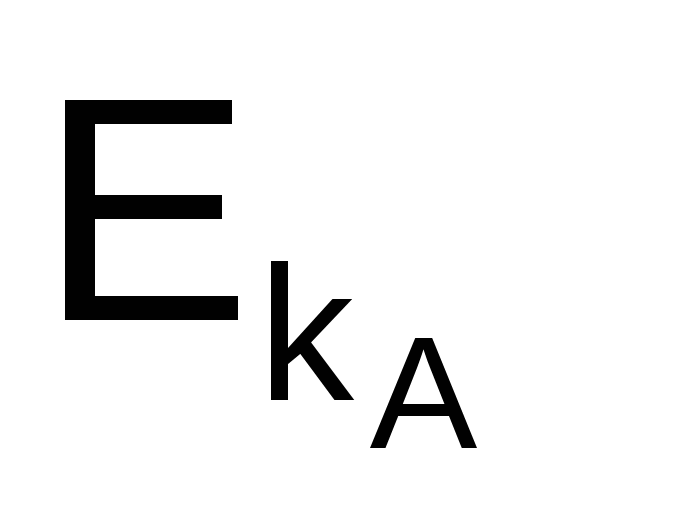 (Т), (Т), 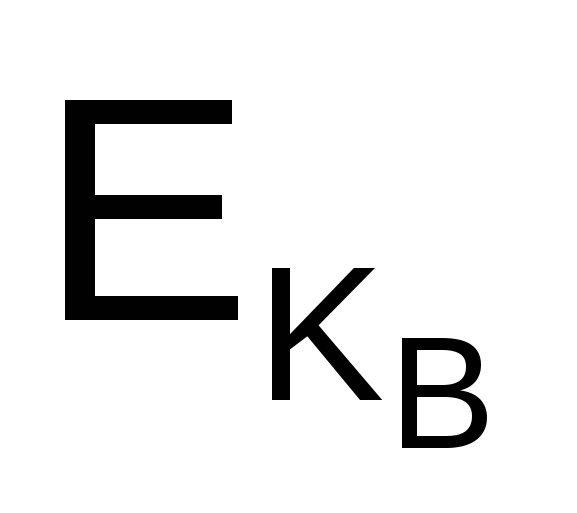 (r1). (r1).
Здесь
СА – сертификат открытого ключа пользователя А;
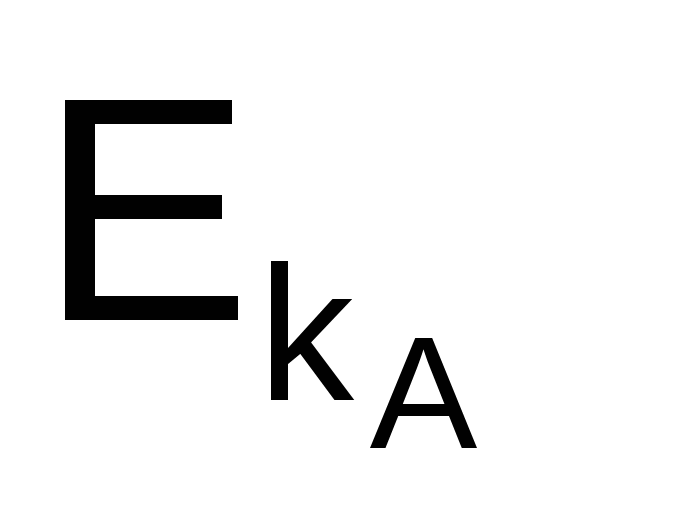 (Т) – отметка времени, зашифрованная секретным ключом участника А и являющаяся подписью участника А, поскольку никто другой не может создать такую подпись; (Т) – отметка времени, зашифрованная секретным ключом участника А и являющаяся подписью участника А, поскольку никто другой не может создать такую подпись;
r1 – случайное число, генерируемое А и используемое для обмена с В в ходе процедуры подлинности.
Если сертификат СА и подпись А верны, то участник В уверен, что сообщение пришло от А. Часть сообщения 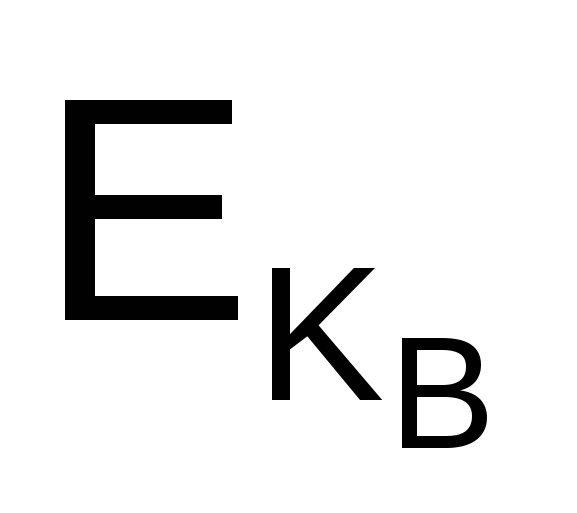 (r1) может расшифровать только В, поскольку никто другой не знает секретного ключа kВ, соответствующего открытому ключу КВ. Участник В расшифровывает значение числа r1 и, чтобы подтвердить свою подлинность, посылает участнику А сообщение (r1) может расшифровать только В, поскольку никто другой не знает секретного ключа kВ, соответствующего открытому ключу КВ. Участник В расшифровывает значение числа r1 и, чтобы подтвердить свою подлинность, посылает участнику А сообщение
(4) В ® А :  (r1). (r1).
Участник А восстанавливает значение r1, расшифровывая это сообщение с использованием своего секретного ключа kА. Если это ожидаемое значение r1, то А получает подтверждение, что вызываемый участник действительно В.
Протокол, основанный на симметричном шифровании, функционирует быстрее, чем протокол, основанный на криптосистемах с открытыми ключами. Однако способность систем с открытыми ключами генерировать цифровые подписи, обеспечивающие различные функции защиты, компенсирует избыточность требуемых вычислений.
79
9.1.8. Прямой обмен ключами между пользователями
При использовании для информационного обмена криптосистемы с симметричным секретным ключом два пользователя, желающие обменяться криптографически защищенной информацией, должны обладать общим секретным ключом. Пользователи должны обменяться общим ключом по каналу связи безопасным образом. Если пользователи меняют ключ достаточно часто, то доставка ключа превращается в серьезную проблему.
Для решения этой проблемы можно применить два способа:
1) использование криптосистемы с открытым ключом для шифрования и передачи секретного ключа симметричной криптосистемы;
2) использование системы открытого распределения ключей Диффи–Хеллмана.
9.2. Алгоритм открытого распределения ключей
Диффи–Хеллмана.
Алгоритм Диффи–Хеллмана был первым алгоритмом с открытыми ключами (предложен в 1976 г.). Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости дискретного возведения в степень в том же конечном поле.
Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.
1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе g Î ZN,
(1 £ g £ N –1), который образует все ненулевые элементы множества ZN, т.е.
{
80
g, g2, ..., gN–1 =1} = ZN – {0}.
Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.
2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи kА и kВ (kА и kВ – случайные большие целые числа, которые хранятся пользователями А и В в секрете).
3. Далее пользователь А вычисляет открытый ключ
yA = 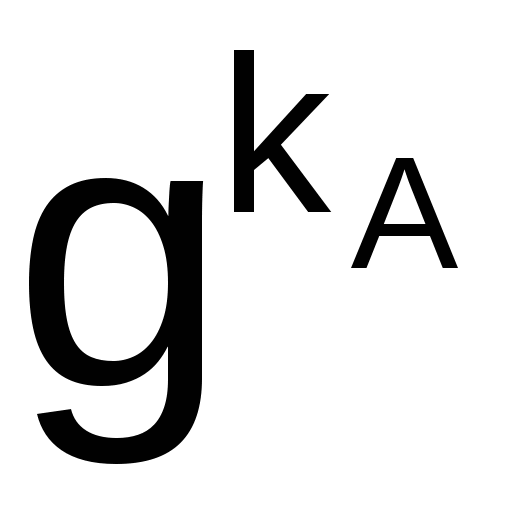 (mod N), (mod N),
а пользователь В – открытый ключ
yВ = 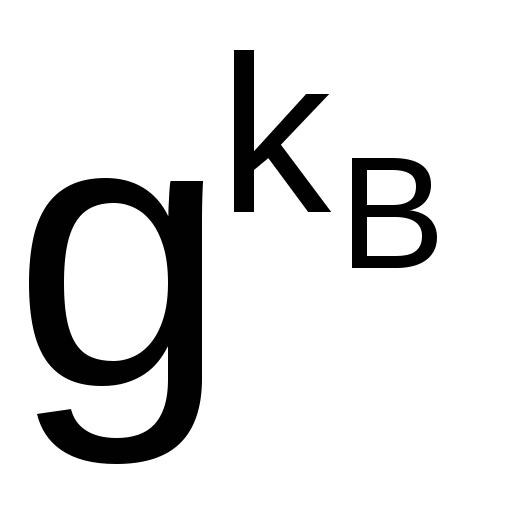 (mod N). (mod N).
4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей yA и yВ по незащищенному каналу. (Мы считаем, что все данные, передаваемые по незащищенному каналу связи, могут быть перехвачены злоумышленником.)
5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие сравнения:
пользователь А: К = 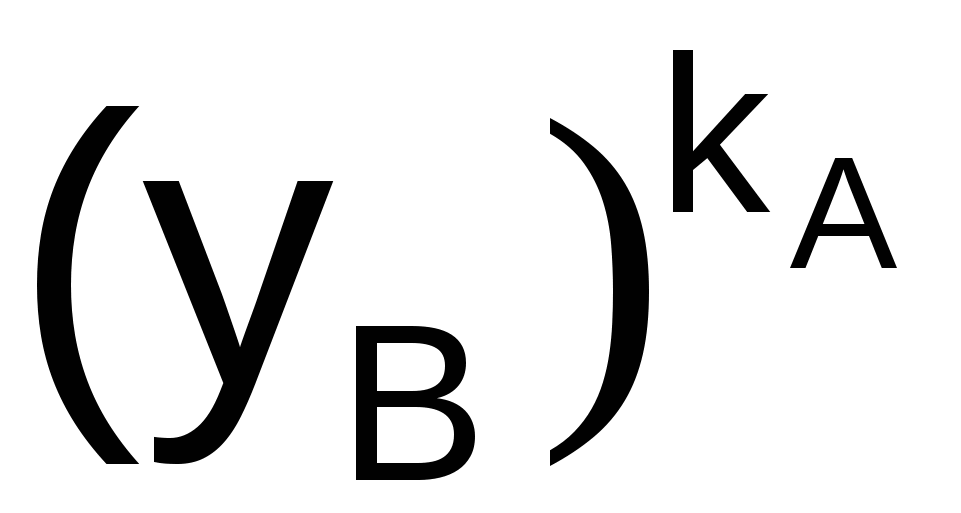 = = 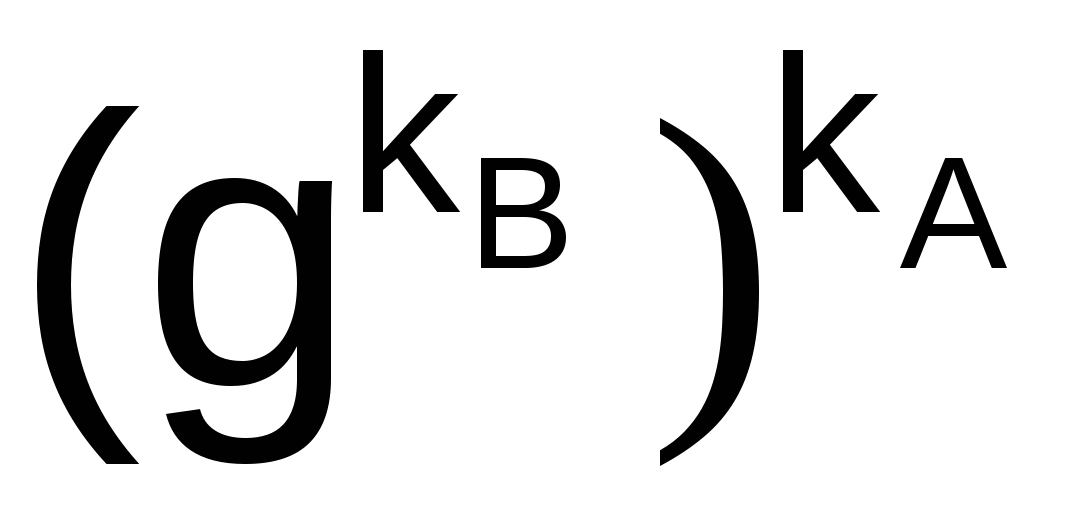 (mod N); (mod N);
пользователь В: К´ = 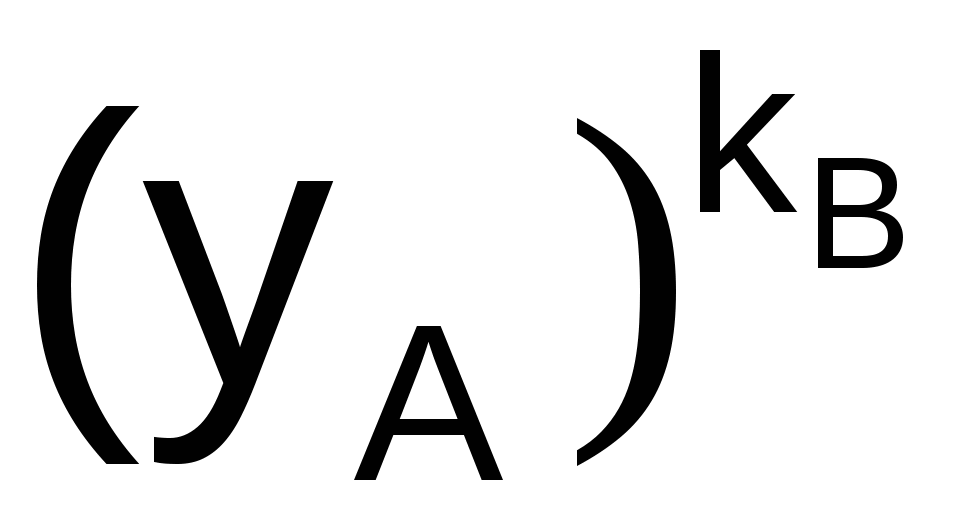 = = 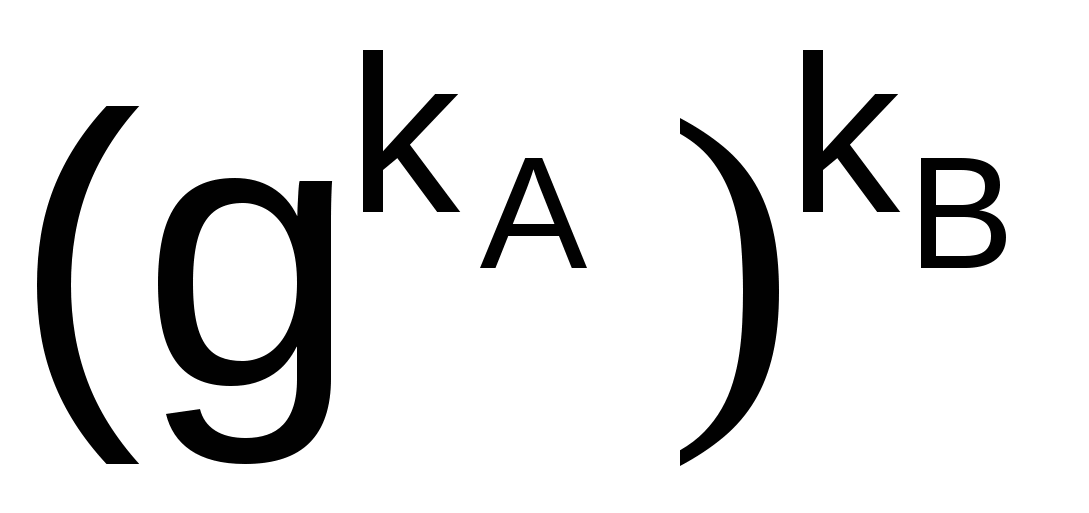 (mod N). (mod N).
При этом К = К´, так как 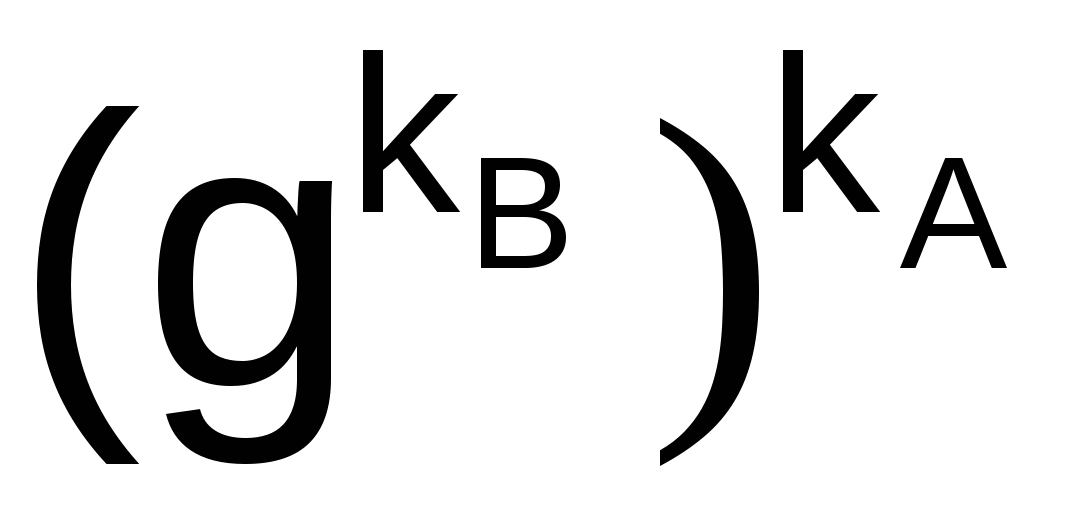 = = 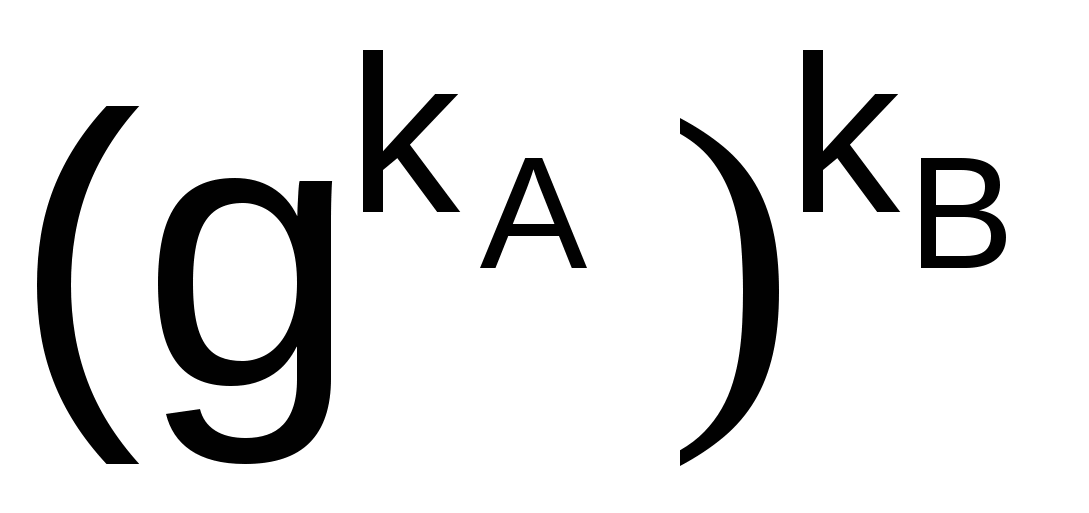 (mod N). (mod N).
Схема реализации алгоритма Диффи–Хеллмана показана на рис. 4.5.
Ключ К может использоваться в качестве общего секретного ключа (ключа шифрования ключей) в симметричной криптосистеме.
Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA): С = ЕK (М) = МК (mod N).
Для выполнения расшифрования получатель сначала находит ключ расшифрования К* с помощью сравнения
К * К* º 1 (mod N –1),
81
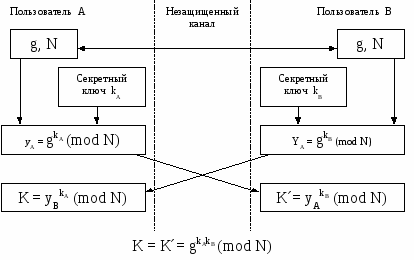
Рисунок 4.5- Схема реализации алгоритма Диффи– Хеллмана
а затем восстанавливает сообщение
М = DK (C) = CK*(mod N).
Злоумышленник, перехватив значения N, g, yА и yВ, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения kА по N, g, yА, что 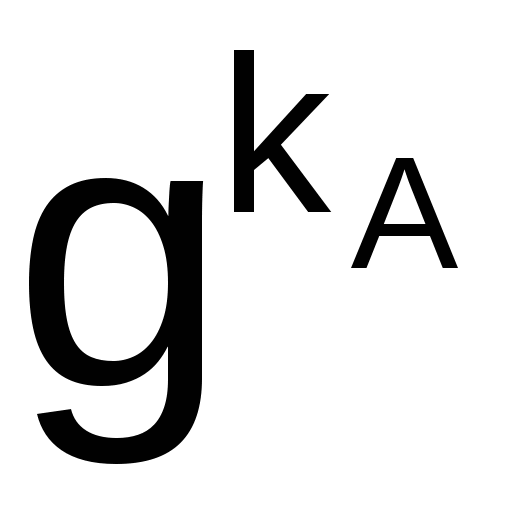 mod N = yА (поскольку в этом случае, вычислив kА, можно найти К= mod N = yА (поскольку в этом случае, вычислив kА, можно найти К=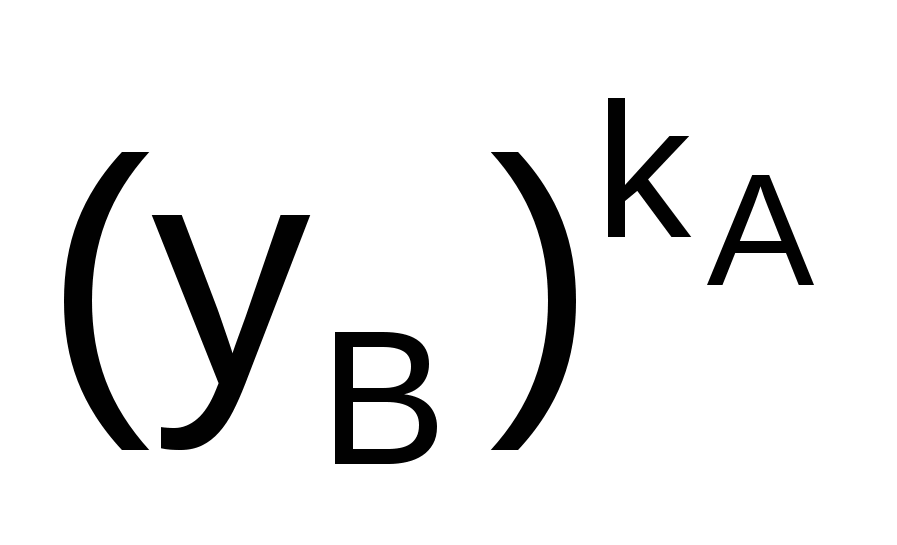 mod N). Однако нахождение kА по N, g и yА – задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой. mod N). Однако нахождение kА по N, g и yА – задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.
В
82
ыбор значений N и g может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N –1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества ZN. (В принципе достаточно, чтобы число g генерировало большую подгруппу мультипликативной группы по mod N.)
Алгоритм открытого распределения ключей Диффи– Хеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи,которой подписываются сообщения об открытом ключе.
Метод Диффи–Хеллмана дает возможность шифровать данные при каждом сеансе связи на новых ключах. Это позволяет не хранить секреты на дискетах или других носителях. Не следует забывать, что любое хранение секретов повышает вероятность попадания их в руки конкурентов или противника.
Преимущество метода Диффи–Хеллмана по сравнению с методом RSA заключается в том, что формирование общего секретного ключа происходит в сотни раз быстрее. В системе RSA генерация новых секретных и открытых ключей основана на генерации новых простых чисел, что занимает много времени.
|
|
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.