|
|
Методичка МОИБ.. Методические разработки к лабораторным работам по дисциплине средства обеспечения информационной безопасности в сетях передачи данных для студентов специальностей 200900, 201000, 201800
Л
26
абораторная работа №2
ИЗУЧЕНИЕ АЛГОРИТМА ШИФРОВАНИЯ С ОТКРЫТЫМ КЛЮЧОМ RSA
1. Цель работы
Изучить принципы и процедурные аспекты криптосистемы RSA.
2. Рекомендуемые источники
1.Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина.- 2-е изд.. перераб. и доп..-М.: Радио и связь, 2001, с. 131-138.
2.Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах.- М.: ДМК Пресс, 2002, с. 204-206.
3.Б. Шнайер. Прикладная криптография.-М.: Триумф, 2002, с. 521-530.
3. Подготовка к работе
1.Ознакомиться с алгоритмом шифрования по одному из рекомендованных источников/1-3/.
2.Ознакомиться с содержанием данной методической
разработки.
3.Подготовить бланк отчета, который должен содержать:
- цель работы;
- основные математические соотношения формирования ключевой информации.
4. Контрольные вопросы
И
27
зобразите обобщенную схему асимметричной криптосистемы.
Характерные особенности асимметричных криптосистем.
Основные требования, обеспечивающие безопасность асимметричной криптосистемы.
Понятие однонаправленных функций.
Сущность алгоритма шифрования RSA.
Сущность процедуры шифрования в системе RSA.
Сущность процедуры расшифрования в системе RSA.
Требования, предъявляемые к исходным параметрам системы RSA для формирования ключевой информации.
5. Содержание работы
Ознакомиться с алгоритмом RSA и его основными особенностями.
Изучить основные этапы шифрования на компьютерной модели.
Произвести установку открытых и закрытых ключей для двух абонентов.
Произвести двухсторонний обмен информацией.
6. Содержание отчета
Отчет должен содержать:
Цель работы.
Структурную схему асимметричной криптосистемы с открытым ключом.
Основные математические соотношения формирования ключевой информации.
Таблицы шифрования и дешифрования.
Выводы о технических возможностях, особенностях, преимуществах и областях применения алгоритма RSA.
7. Методические указания к выполнению работы
Л
28
абораторная работа выполняется на ПЭВМ в режиме диалога. Все операции программа выполняет в 64 разрядном формате со знаком, т.е. допускается максимальный размер операндов 263 – 1 = 9,2 ∙1018. Однако, с учетом того, что в вычислениях имеются операции умножения, значения операндов-сомножителей не должно превышать значений 3 ∙109. В лабораторной программе используются числа, содержащие не более 7-8 разрядов.
Лабораторная работа выполняется в двух рабочих окнах. Сначала в окне, совмещенном с главным меню, определяются численные значения параметров криптосистемы RSA для двух участников обмена информацией. Затем в окне «Передача сообщений по методу RSA», которое вызывается из главного меню по пункту «Шифр RSA»→«Обмен сообщениями» задаются цифровые сообщения, устанавливаются значения ключей и осуществляется обмен засекреченными сообщениями.
8. Лабораторное задание
1.Вывести таблицу простых чисел. Для этого в главном меню выбрать пункт «Опции», а затем – пункт «Простые числа», после запуска которого на экране появится рабочее окно «Последовательность простых чисел». После нажатия клавиши «Сформировать ряд простых чисел на экране появится таблица, содержащая 1000 простых чисел от 3 до 7927.
2.Для двух участников обмена зашифрованными сообщениями А (Анна) и Б (Боб) выбрать из таблицы две пары простых чисел p и q, причем p≠q.
3.Для обоих участников вычислить значения модуля Na и Nb и функции Эйлера
fEa и fEb по соотношениям:
N = pq
f
29
E = (p-1)(q-1)
4.Для обоих участников выбрать значения закрытых ключей Da и Db, которые должны быть взаимно простыми с соответствующими функциями Эйлера, т.е. Da c fEa и Db c fEb. Проще всего это сделать, если в качестве D выбрать из таблицы простое число
1< D < fE и проверить, что fE не делится на D.
5.Выбранные и вычисленные значения Na, fEa, Da, Nb, fEb, Db заносятся в соответствующие позиции главного окна.
6.Нажатием клавиши «Найти открытый ключ» запускается программа вычисления открытых ключей Еa и Eb, удовлетворяющих условию ED = 1 (mod fE).
7.После заполнения всех 8 позиций главного окна процедура формирования ключей считается законченной.
8.Проверить, что полученное значение открытого ключа Е и значение модуля N -взаимно простые числа по методике п. 4.
9.Для обмена сообщениями перейти во второе окно, выбрав пункт «Обмен сообщениями» основного меню.
10.Для пользователя А (Анна) записать в цифровой форме передаваемое сообщение в позицию М (Message) (4 знака) при условии M
В
30
нимание! Распространенная ошибка пользователей криптосистемы RSA заключается в путанице, где чьи ключи использовать. Поэтому при работе во втором окне позиции N,E, и D указаны без индексов a и b. Нужно иметь в виду, что для зашифрования у отправителя (Анны) используется открытый ключ (N и Е), а для расшифрования у получателя (Боба) используется тайный ключ (N и D)/
11.Произвести процесс выбора ключей для передачи сообщений от Анны к Бобу и ответа от Боба к Анне трижды для 6-и, 7-и и 8 значных значений модуля N. Все значения ключей и сообщений (в открытом и зашифрованном виде) зафиксировать и занести в таблицу и отметить продолжительность процедур.
12.Провести наблюдение за процессом засекреченной передачи при несоблюдении следующих условий:
- выбор в качестве ключа D не простого числа;
- (ED) ≠1 (mod fE).
9. Общие сведения
9.1. Концепция криптосистемы с открытым ключом
Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования – другой ключ (отсюда и название – асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.
Для расшифрования данных получатель зашифрованной информации использует второйключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.
О
31
бобщенная схема асимметричной криптосистемы с открытым ключом показана на рис.2.1. В этой криптосистеме применяют два различных ключа: Кв – открытый ключ отправителя А; kв – секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ kв по незащищенному каналу). Значения ключей Кв и kв зависят от начального состояния генератора ключей.
Раскрытие секретного ключа kв по известному открытому ключу Кв должно быть вычислительно неразрешимой задачей.
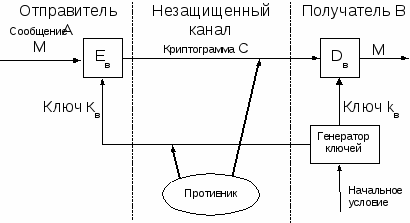
Рисунок 2.1- Обобщенная схема асимметричной криптосистемы с открытым ключом
Характерные особенности асимметричных криптосистем:
1. Открытый ключ Кв и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны Кв и С.
2. Алгоритмы шифрования и расшифрования
Ев : М С,
Dв : С М
я
32
вляются открытыми.
Защита информации в асимметричной криптосистеме основана на секретности ключа kв.
У.Диффи и М.Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:
1. Вычисление пары ключей (Кв, kв) получателем В на основе начального условия должно быть простым.
2. Отправитель А, зная открытый ключ Кв и сообщение М, может легко вычислить криптограмму
С = 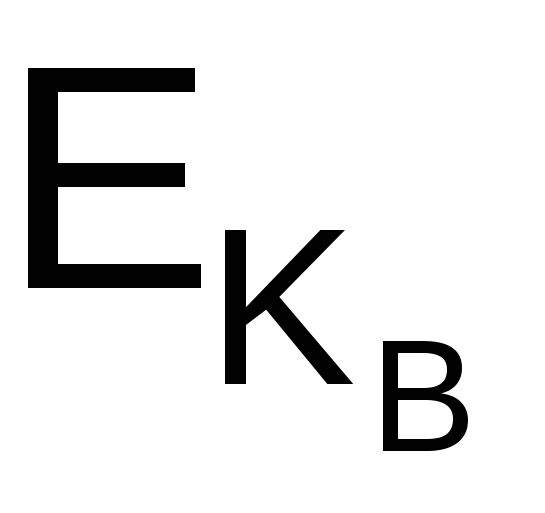 (М) = Ев (М) (2.1) (М) = Ев (М) (2.1)
3. Получатель В, используя секретный ключ kв и криптограмму С, может легко восстановить исходное сообщение
М = 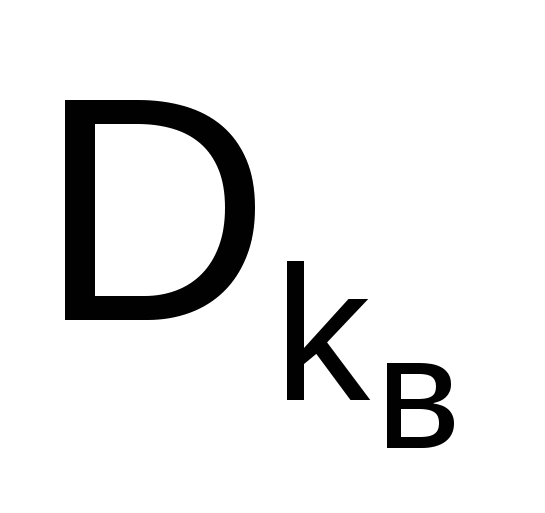 (С) = Dв(С) = Dв [Ев(М)] (2.2) (С) = Dв(С) = Dв [Ев(М)] (2.2)
4. Противник, зная открытый ключ Кв, при попытке вычислить секретный ключ kв наталкивается на непреодолимую вычислительную проблему.
5. Противник, зная пару (Кв, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему.
9.2. Однонаправленные функции
Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Неформально однонаправленную функцию можно определить следующим образом. Пусть X и Y – некоторые произвольные множества. Функциf : X Y
является однонаправленной, если для всех xX можно легко вычислить функцию
y = f (x), где yY.
И
33
в то же время для большинства yY достаточно сложно получить значение xX, такое, что f (x)=y (при этом полагают, что существует по крайней мере одно такое значение x).
Основным критерием отнесения функции f к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования
Y X.
В качестве первого примера однонаправленной функции рассмотрим целочисленное умножение. Прямая задача – вычисление произведения двух очень больших целых чисел P и Q, т.е. нахождение значения
N = PQ (2.3)
является относительно несложной задачей для ЭВМ.
Обратная задача – разложение на множители большого целого числа, т.е. нахождение делителей P и Q большого целого числа N = PQ, является практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел при целом N2664 и PQ для разложения числа N потребуется около 1023 операций, т.е. задача практически неразрешима на современных ЭВМ.
Следующий характерный пример однонаправленной функции – это модульная экспонента с фиксированными основанием и модулем. Пусть A и N – целые числа, такие, что 1 А < N. Определим множество ZN:
ZN = {0, 1, 2, ..., N –1}.
Тогда модульная экспонента с основанием А по модулю N представляет собой функцию
fA,N : ZN ZN,
fA,N (x) = Ax (mod N) (2.4),
где X – целое число, 1 x N –1.
Существуют эффективные алгоритмы, позволяющие достаточно быстро вычислить значения функции fA,N (x).
Е
34
сли y = Ax, то естественно записать x = logA (у).
Поэтому задачу обращения функции fA,N(x) называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.
Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, y найти целое число x, такое, что
Ax mod N = y.
Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.
По современным оценкам теории чисел при целых числах A 2664 и N 2664 решение задачи дискретного логарифмирования (нахождение показателя степени x для известного y) потребует около 1026 операций, т.е. эта задача имеет в 103 раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.
Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.
Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с "потайным ходом" (с лазейкой). Дадим неформальное определение такой функции. Функция
f : X Y
о
35
тносится к классу однонаправленных функций с "потайным ходом" в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен "потайной ход" (секретное число, строка или другая информация, ассоциирующаяся с данной функцией).
В качестве примера однонаправленной функции с "потайным ходом" можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для указания числового значения сообщения М либо криптограммы С.
9.3. Криптосистема шифрования данных RSA
Алгоритм RSA предложили в 1978 г. три автора: Р.Райвест (Rivest), А.Шамир (Shamir) и А.Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи.
Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.
В криптосистеме RSA открытый ключ Кв, секретный ключ kв, сообщение М и криптограмма С принадлежат множеству целых чисел
ZN = {0, 1, 2, ..., N –1}, (2.5)
где N – модуль:
N = PQ (2.6) .
Здесь P и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают P и Q равной длины и хранят в секрете.
Множество ZN с операциями сложения и умножения по модулю N образует арифметику по модулю N.
О
36
ткрытый ключ Кв выбирают случайным образом так, чтобы выполнялись условия:
1< Кв (N), НОД (Кв, (N)) =1, (2.7)
(N)=(P –1) (Q –1), (2.8)
где (N) – функция Эйлера.
Функция Эйлера (N) указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно проcты с N.
Второе из указанных выше условий означает, что открытый ключ Кв и функция Эйлера (N) должны быть взаимно простыми.
Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ kв, такой, что
kв Кв 1 (mod (N)) (2.9)
или
kв = Кв–1 (mod (P –1)(Q –1)).
Это можно осуществить, так как получатель В знает пару простых чисел (P,Q) и может легко найти (N). Заметим, что kв и N должны быть взаимно простыми.
Открытый ключ Кв используют для шифрования данных, а секретный ключ kв – для расшифрования.
Преобразование шифрования определяет криптограмму С через пару (открытый ключ Кв, сообщение М) в соответствии со следующей формулой:
C = 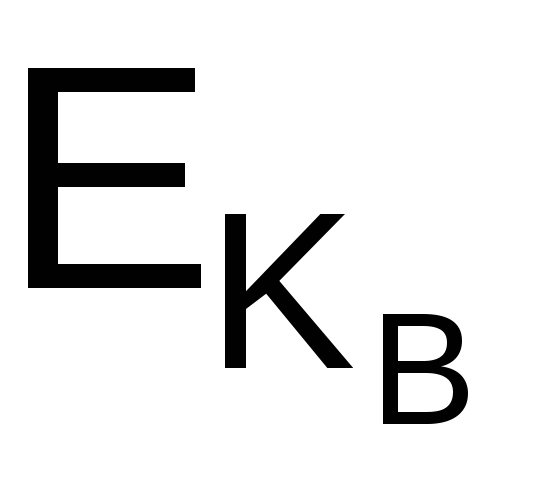 (M) = EВ (M) = (M) = EВ (M) = 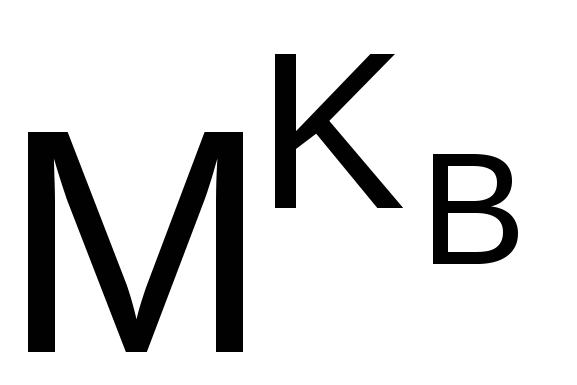 (mod N). (2.10) (mod N). (2.10)
В качестве алгоритма быстрого вычисления значения C используют ряд последовательных возведений в квадрат целого M и умножений на M с приведением по модулю N.
Обращение функции C = 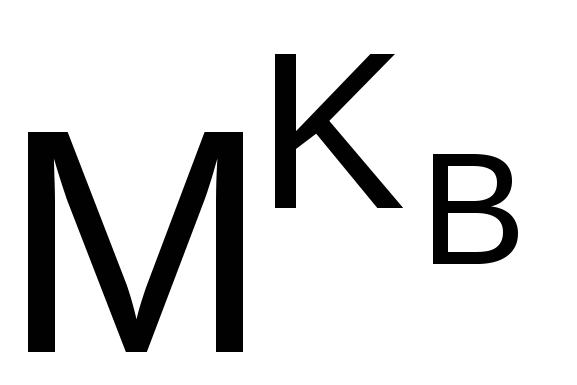 (mod N), т.е. определение значения M по известным значениям C, Кв и N, практически не осуществимо при N 2 512. (mod N), т.е. определение значения M по известным значениям C, Кв и N, практически не осуществимо при N 2 512.
О
37
днако обратную задачу, т.е. задачу расшифрования криптограммы С, можно решить, используя пару (секретный ключ kв, криптограмма С) по следующей формуле:
М = 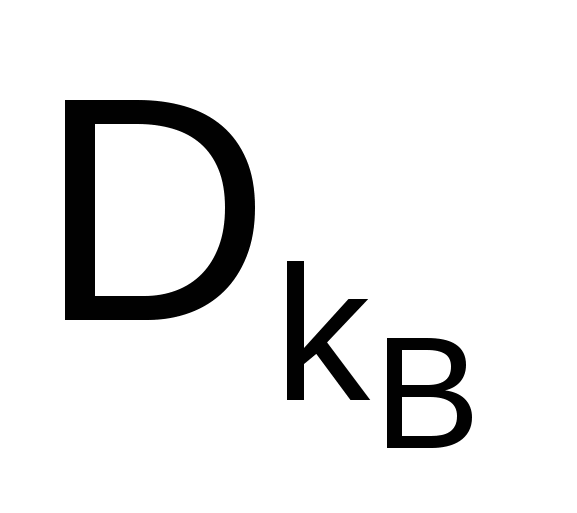 (С) = DВ (C) = (С) = DВ (C) = 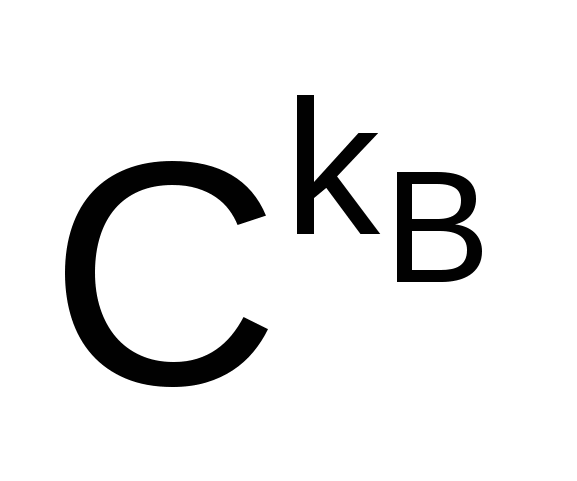 (mod N). (2.11) (mod N). (2.11)
Процесс расшифрования можно записать так:
DВ(EВ (М)) = М. (2.12)
Подставляя в (2.12) значения (2.10) и (2.11), получаем:
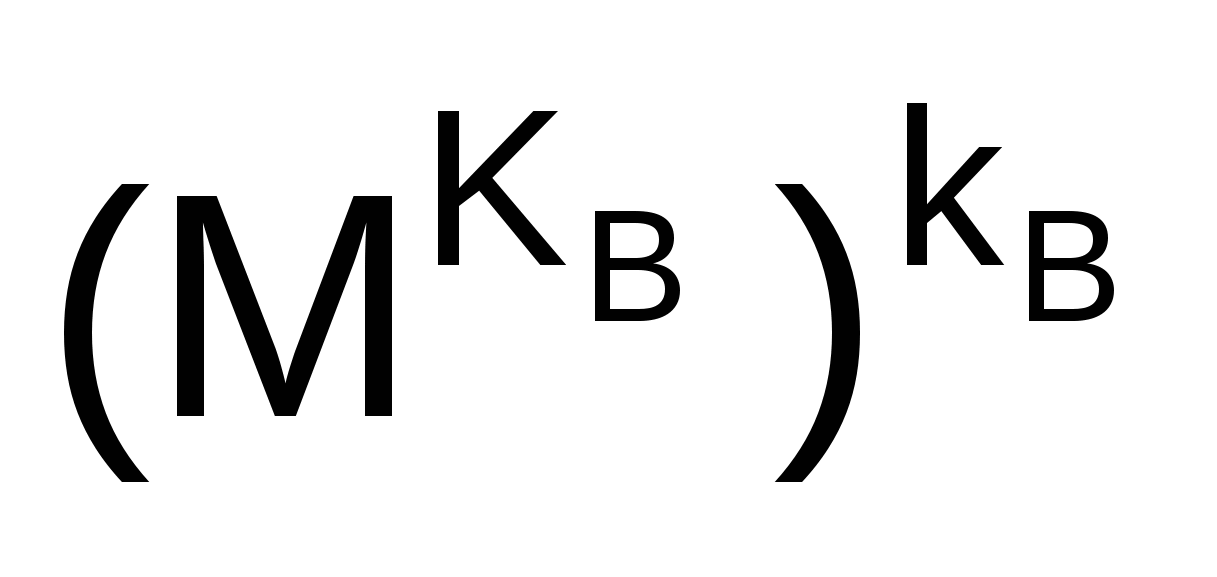 = М (mod N) = М (mod N)
или
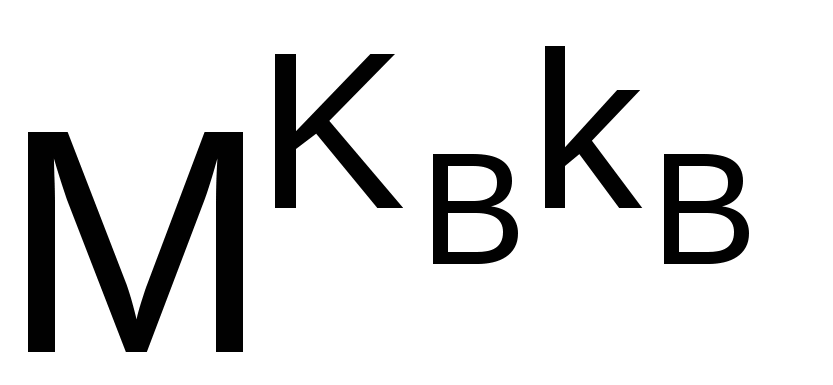 = M (mod N). (2.13) = M (mod N). (2.13)
Величина (N) играет важную роль в теореме Эйлера, которая утверждает, что если НОД (x, N) =1, то
x(N) 1 (mod N),
или в несколько более общей форме
xn(N)+1 x (mod N). (2.14)
Сопоставляя выражения (2.13) и (2.14), получаем
Кв kв = n (N) +1
или, что то же самое,
Кв kв 1 (mod (N)).
Именно поэтому для вычисления секретного ключа kв используют соотношение (2.9).
Таким образом, если криптограмму
C = 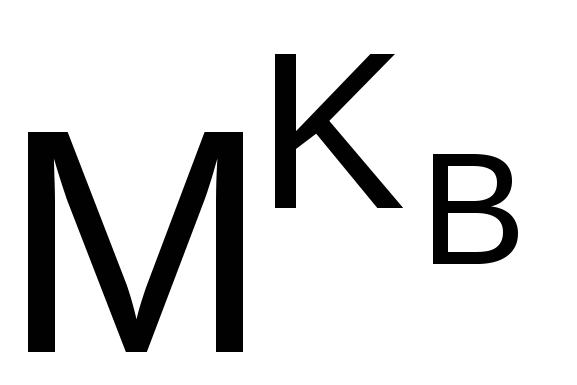 (mod N) (mod N)
возвести в степень kв, то в результате восстанавливается исходный открытый текст М, так как
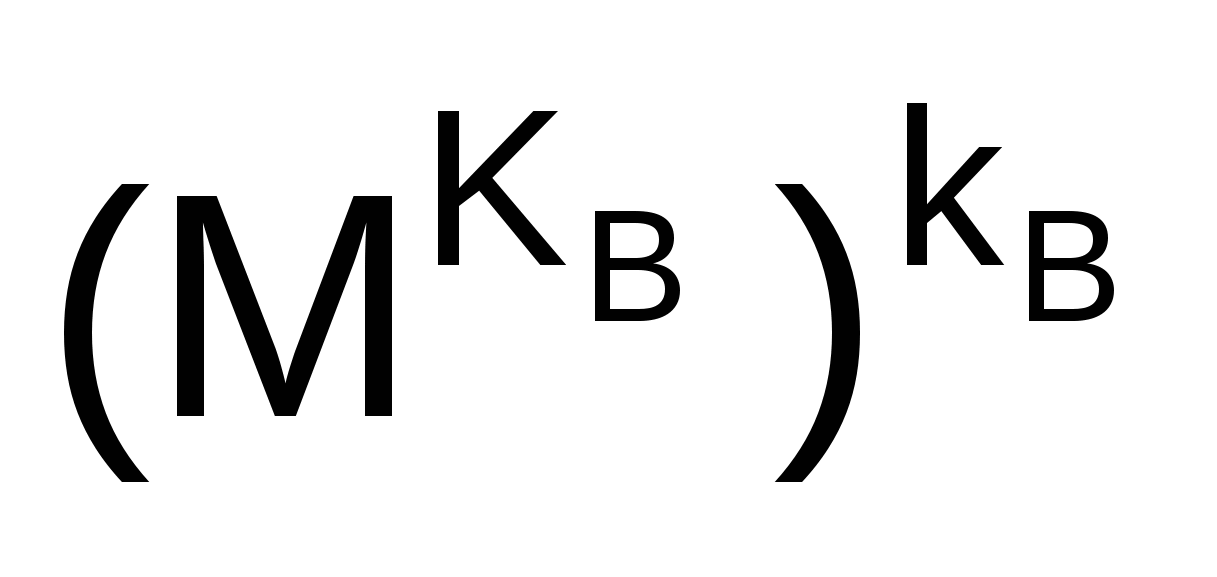 = = 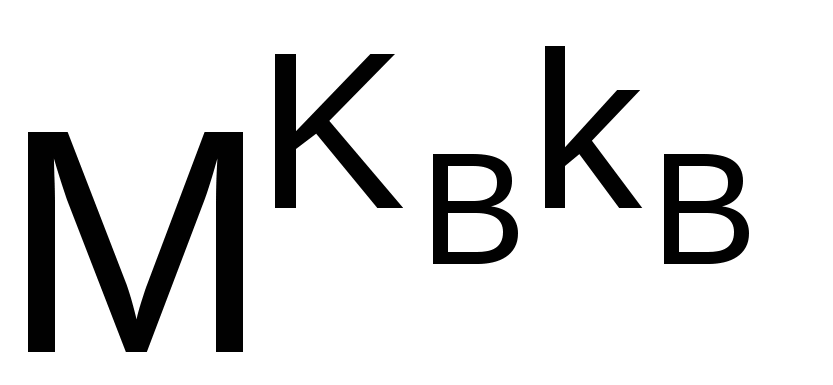 = Mn(N)+1 M (mod N). = Mn(N)+1 M (mod N).
Таким образом, получатель В, который создает криптосистему, защищает два параметра: 1) секретный ключ kв и 2) пару чисел (P,Q), произведение которых дает значение модуля N. С другой стороны, получатель В открывает значение модуля N и открытый ключ Кв.
Противнику известны лишь значения Кв и N. Если бы он смог разложить число N на множители P и Q, то он узнал бы "потайной ход" – тройку чисел {P,Q,Кв}, вычислил значение функции Эйлера
38
(N) = (P –1) (Q –1)
и определил значение секретного ключа kв.
Однако, как уже отмечалось, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных P и Q составляют не менее 100 десятичных знаков).
9.4. Процедуры шифрования и расшифрования в криптосистеме RSA
Предположим, что пользователь А хочет передать пользователю В сообщение в зашифрованном виде, используя криптосистему RSA. В таком случае пользователь А выступает в роли отправителя сообщения, а пользователь В – в роли получателя. Как отмечалось выше, криптосистему RSA должен сформировать получатель сообщения, т.е. пользователь В. Рассмотрим последовательность действий пользователя В и пользователя А.
1. Пользователь В выбирает два произвольных больших простых числа P≠Q.
2. Пользователь В вычисляет значение модуля N = P * Q.
3. Пользователь В вычисляет функцию Эйлера
(N) = (P –1) (Q –1)
и выбирает случайным образом значение открытого ключа Кв с учетом выполнения условий:
1< Кв (N), НОД (Кв, (N)) =1.
4. Пользователь В вычисляет значение секретного ключа kв, используя расширенный алгоритм Евклида при решении сравнения
kв Кв–1 (mod (N)).
5. Пользователь В пересылает пользователю А пару чисел (N, Кв) по незащищенному каналу.
Е
39
сли пользователь А хочет передать пользователю В сообщение М, он выполняет следующие шаги.
6. Пользователь А разбивает исходный открытый текст М на блоки, каждый из которых может быть представлен в виде числа
Мi = 0, 1, 2, ..., N –1.
7. Пользователь А шифрует текст, представленный в виде последовательности чисел Мi по формуле
Ci = 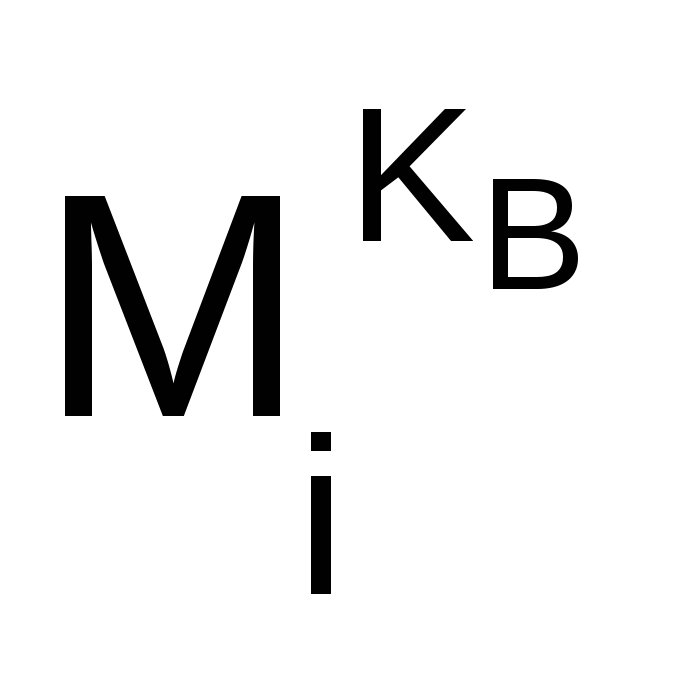 (mod N) (mod N)
и отправляет криптограмму
С1, С2, С3, ..., Ci, ...
пользователю В.
8. Пользователь В расшифровывает принятую криптограмму
С1, С2, С3, ..., Ci, ...,
используя секретный ключ kв, по формуле
Мi = 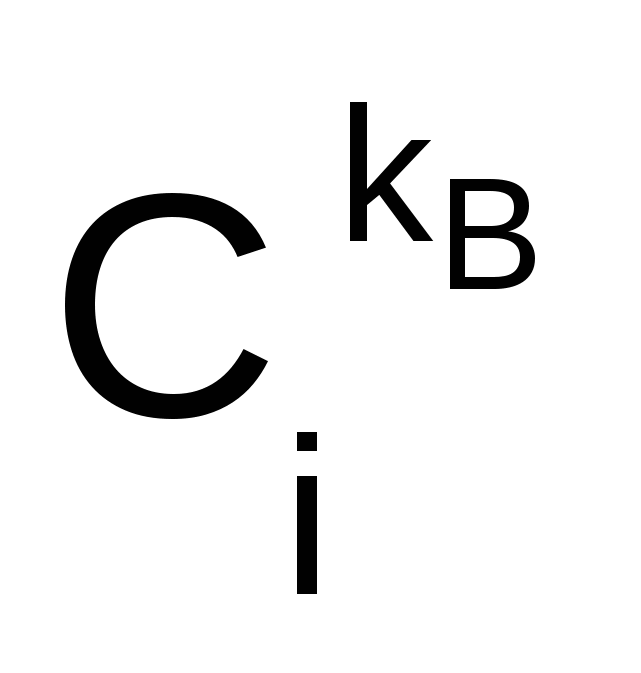 (mod N). (mod N).
В результате будет получена последовательность чисел Мi, которые представляют собой исходное сообщение М. Чтобы алгоритм RSA имел практическую ценность, необходимо иметь возможность без существенных затрат генерировать большие простые числа, уметь оперативно вычислять значения ключей Кв и kв.
|
|
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.