Методичка МОИБ.. Методические разработки к лабораторным работам по дисциплине средства обеспечения информационной безопасности в сетях передачи данных для студентов специальностей 200900, 201000, 201800
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Государственное образовательное учреждение высшего профессионального образования «Поволжская государственная академия телекоммуникаций и информатики» Кафедра ПДС Методические разработки к лабораторным работам по дисциплине «СРЕДСТВА ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ» для студентов специальностей 200900, 201000, 201800 Самара, 2005 Методические разработки к лабораторным работам по дисциплине «Средства обеспечения информационной безопасности в сетях передачи данных» / Сост. к.т.н., доц. А.В.Крыжановский, д.т.н.,проф.А.А. Нерсесянц -Самара, 2005.-140 с. , ил. Приведены методические указания к лабораторным работам, относящимся к основным разделам криптографии: симметричные и асимметричные криптосистемы, электронная цифровая подпись, управление криптографическими ключами и идентификация. Все методические указания снабжены краткими теоретическими сведениями. Методические разработки утверждены на заседании кафедры ПДС 7.06.2005 г.,протокол № 8. Редактор- д.т.н., проф. Б.Я.Лихтциндер Рецензент-д.т.н. проф. В.Г. Карташевский Лабораторная работа №1ИЗУЧЕНИЕ ОТЕЧЕСТВЕННОГО СТАНДАРТА ШИФРОВАНИЯ ГОСТ 28147-89 1. Цель работы Изучить основные принципы и особенности симметричного алгоритма шифрования по стандарту ГОСТ 28147-89. 2. Рекомендуемые источники
3. Подготовка к работе
- 3 цель работы; - блок-схему алгоритма в режиме простой замены; - заготовки таблиц по п.8 задания; - объяснение результатов шифрования и дешифрования. 4. Контрольные вопросы
5. Содержание работы
6. Содержание отчета
7. Методические указания к выполнению работы Лабораторная работа выполняется на ПЭВМ в диалоговом режиме. После запуска программы Zinf на экране монитора возникает главное меню, на котором нужно выбрать пункт GOST 28147. Возврат в главное меню и выход из него осуществляется кнопкой EXIT. Программа Zinf не контролирует ввод некорректных данных и ошибочных действий пользователя, поэтому требуется внимательность, а для выхода из тупиковых ситуаций нужно воспользоваться кнопкой EXIT. Лабораторная программа ГОСТ имитирует процедуры, установленные стандартом для шифрования в режиме простой замены. Ш 5 ифруемый 64-х разрядный блок информации вводится в окна «Блок №1» и «Блок №2» в шестнадцатеричном коде, по 8 шестнадцатеричных цифр в каждое окно. Ввод большего числа цифр программа воспринимает как ошибку. Соответствие десятичных, двоичных и шестнадцатеричных чисел представлено в табл. 1-1. Таблица 1.1-Соответствие чисел в различных кодах
Ключ, состоящий из 256 разрядов, вводится в 8 окон также в шестнадцатеричном коде по 8 цифр в каждое окно (Кл. ХО, Х!, …,Х7). В программе для наблюдения за процессом обработки данных, реализованы 2 варианта работы: —основной вариант – клавиши «Зашифровать» обеспечивают штатный режим, при котором основной цикл (зашифрование и расшифрование одним из ключей) выполняется непрерывно 32 раза; —учебный вариант (шаговый режим) – цикл разбит на 5 этапов: суммирование по mod 32, подстановка, сдвиг, суммирование по mod 2, перепись. Нажимая на соответствующие клавиши, можно последовательно наблюдать за поэтапным процессом шифрования. Для упрощения программы в учебном варианте используется только подключ ХО, что соответствует варианту 8 одинаковых подключей. Д 6 ругой особенностью программы является вариант реализации подстановок. Стандарт рекомендует для каждой тетрады 32-х разрядного слова S использовать различные варианты секретных таблиц-подстановок (8 таблиц). В данной учебной программе для ее упрощения реализована одна таблица замен:0→F, 1→E, 2→D, 3→C, 4→B, 5→A, 6→9, 7→8, 8→7, 9→6, A→5, B→4, C→3, D→2, E→1, F→0. В лабораторной программе в целях изучения влияния на качество шифрования подстановок и перестановок (сдвигов), есть возможность отключать любой из этих этапов с помощью флажков. Еще раз обратите внимание на то, что в окна информационных блоков и ключей нельзя вводить больше 8 цифр (меньше – можно) и нельзя делать пробелы в словах. 8. Лабораторное задание 1.Нажатием клавиши ТЕСТ произвести тестовую загрузку информации и ключей. Освоить работу программы шифрования во всех ее вариантах. 2.Проверить реализацию в данном алгоритме принципа: «Изменение одного символа (бита) в информации должно распространиться на большое число символов криптограммы». Для этого: - ввести тестовую комбинацию; - зашифровать информацию и записать криптограмму в двоичном коде (64 разряда); - изменить один бит в одном из информационных блоков; - 7 провести шифрование в четырех вариантах в зависимости от включения или выключения флажков-этапов подстановки и сдвига. Записать полученные результаты в двоичном коде. 3.Проверить аналогично, реализацию принципа «Изменение одного символа ключа должно распространяться на большое число знаков криптограммы». 4.Проверить работу алгоритма шифрования при «плохих» ключах. Например, ключи из одних нулей (64 шестнадцатеричных «0») или из одних единиц (64 цифры «F»). Записать для каждого случая варианта (по включению флажков) криптограммы в шестнадцатеричном и двоичном кодах. 9. Общие сведения 9.1. Принципы криптографической защиты информации Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы сделать эти данные бесполезными для противника. Такие преобразования позволяют решить две главные проблемы защиты данных: проблему конфиденциальности (путем лишения противника возможности извлечь информацию из канала связи) и проблему целостности (путем лишения противника возможности изменить сообщение так, чтобы изменился его смысл, или ввести ложную информацию в канал связи). Проблемы конфиденциальности и целостности информации тесно связаны между собой, поэтому методы решения одной из них часто применимы для решения другой. О 8 бобщенная схема криптографической системы, обеспечивающей шифрование передаваемой информации, показана на рис.1.1. Отправитель генерирует открытый текст исходного сообщения М, которое должно быть передано законному получателю по незащищенному каналу. За каналом следит перехватчик с целью перехватить и раскрыть передаваемое сообщение. Для того чтобы перехватчик не смог узнать содержание сообщения М, отправитель шифрует его с помощью обратимого преобразования ЕК и получает шифртекст (или криптограмму) С = ЕК (М), который отправляет получателю. 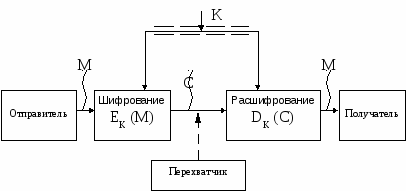  Рисунок1.1- Обобщенная схема криптосистемы Законный получатель, приняв шифртекст С, расшифровывает его с помощью обратного преобразования D = ЕК–1 и получает исходное сообщение в виде открытого текста М: DK (C) = ЕК–1 (ЕК (М)) = M. П 9 реобразование ЕК выбирается из семейства криптографических преобразований, называемых криптоалгоритмами,. Параметр, с помощью которого выбирается отдельное используемое преобразование, называется криптографическим ключом К. Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ компьютера, которые позволяют зашифровать открытый текст и расшифровать шифр-текст различными способами, один из которых выбирается с помощью конкретного ключа К. Говоря более формально, криптографическая система – это однопараметрическое семейство ЕК : из пространства Вообще говоря, преобразование шифрования может быть симметричным или асимметричным относительно преобразования расшифрования. Это важное свойство функции преобразования определяет два класса криптосистем:
Схема симметричной криптосистемы с одним секретным ключом была показана на рис.1.1. В ней используются одинаковые секретные ключи в блоке шифрования и блоке расшифрования. Обобщенная схема асимметричной криптосистемы с двумя разными ключами К1 и К2 показана на рис.1.2. В этой криптосистеме один из ключей является открытым, а другой – секретным. В 10 симметричной криптосистеме секретный ключ надо передавать отправителю и получателю по защищенному каналу распространения ключей, например такому, как курьерская служба. На рис.1.1 этот канал показан "экранированной" линией. Существуют и другие способы распределения секретных ключей, они будут рассмотрены позднее. В асимметричной криптосистеме передают по незащищенному каналу только открытый ключ, а секретный ключ сохраняют на месте его генерации. 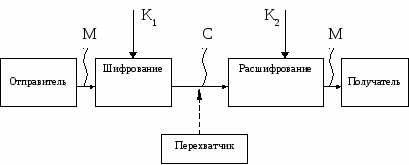 Рисунок 1.2- Обобщенная схема асимметричной криптосистемы с открытым ключом На рис.1.3 показан поток информации в криптосистеме в случае активных действий перехватчика. Активный перехватчик не только считывает все шифртексты, передаваемые по каналу, но может также пытаться изменять их по своему усмотрению. Любая попытка со стороны перехватчика расшифровать шифртекст С для получения открытого текста М или зашифровать свой собственный текст М’ для получения правдоподобного шифртекста С’, не имея подлинного ключа, называется крипто-аналитической атакой. Е 11 сли предпринятые криптоаналитические атаки не достигают поставленной цели и криптоаналитик не может, не имея подлинного ключа, вывести М из С или С’ из М’, то полагают, что такая криптосистема является криптостойкой. 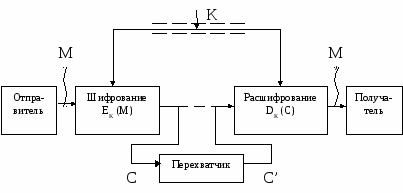 Рисунок1. 3- Поток информации в криптосистеме при активном перехвате сообщений Криптоанализ – это наука о раскрытии исходного текста зашифрованного сообщения без доступа к ключу. Успешный анализ может раскрыть исходный текст или ключ. Он позволяет также обнаружить слабые места в криптосистеме, что, в конечном счете, ведет к тем же результатам. Ф 12 ундаментальное правило криптоанализа, впервые сформулированное голландцем А.Керкхоффом еще в XIX веке заключается в том, что стойкость шифра (криптосистемы) должна определяться только секретностью ключа. Иными словами, правило Керкхоффа состоит в том, что весь алгоритм шифрования, кроме значения секретного ключа, известен криптоаналитику противника. Это обусловлено тем, что криптосистема, реализующая семейство криптографических преобразований, обычно рассматривается как открытая система. Такой подход отражает очень важный принцип технологии защиты информации: защищенность системы не должна зависеть от секретности чего-либо такого, что невозможно быстро изменить в случае утечки секретной информации. Обычно криптосистема представляет собой совокупность аппаратных и программных средств, которую можно изменить только при значительных затратах времени и средств, тогда как ключ является легко изменяемым объектом. Именно поэтому стойкость криптосистемы определяется только секретностью ключа. Другое почти общепринятое допущение в криптоанализе состоит в том, что криптоаналитик имеет в своем распоряжении шифртексты сообщений. Существует четыре основных типа криптоаналитических атак. Конечно, все они формулируются в предположении, что криптоаналитику известны применяемый алгоритм шифрования и шифртексты сообщений. Перечислим эти криптоаналитические атаки. 1. Криптоаналитическая атака при наличии только известных шифртекстов Криптоаналитик имеет только шифртексты С1, С2, …, Сi нескольких сообщений, причем все они зашифрованы с использованием одного и того же алгоритма шифрования ЕК. Работа криптоаналитика заключается в том, чтобы раскрыть исходные тексты М1, М2, …, Мi по возможности большинства сообщений или, еще лучше, вычислить ключ К, использованный для шифрования этих сообщений, с тем, чтобы расшифровать и другие сообщения, зашифрованные этим ключом. 2. Криптоаналитическая атака при наличии известных открытых текстов К 13 риптоаналитик имеет доступ не только к шифртекстам С1, С2, …, Сi нескольких сообщений, но также к открытым текстам М1, М2, …, Мiэтих сообщений. Его работа заключается в нахождении ключа К, используемого при шифровании этих сообщений, или алгоритма расшифрования DК любых новых сообщений, зашифрованных тем же самым ключом. 3. Криптоаналитическая атака при возможности выбора открытых текстов Криптоаналитик не только имеет доступ к шифртекстам С1, С2, …, Сiи связанным с ними открытым текстам М1, М2, …, Мiнескольких сообщений, но и может по желанию выбирать открытые тексты, которые затем получает в зашифрованном виде. Такой криптоанализ получается более мощным по сравнению с криптоанализом с известным открытым текстом, потому что криптоаналитик может выбрать для шифрования такие блоки открытого текста, которые дадут больше информации о ключе. Работа криптоаналитика состоит в поиске ключа К, использованного для шифрования сообщений, или алгоритма расшифрования DК новых сообщений, зашифрованных тем же ключом. 4. Криптоаналитическая атака с адаптивным выбором открытого текста Э 14 то – особый вариант атаки с выбором открытого текста. Криптоаналитик может не только выбирать открытый текст, который затем шифруется, но и изменять свой выбор в зависимости от результатов предыдущего шифрования. При криптоанализе с простым выбором открытого текста криптоаналитик обычно может выбирать несколько крупных блоков открытого текста для их шифрования; при криптоанализе с адаптивным выбором открытого текста он имеет возможность выбрать сначала более мелкий пробный блок открытого текста, затем выбрать следующий блок в зависимости от результатов первого выбора, и т.д. Эта атака предоставляет криптоаналитику еще больше возможностей, чем предыдущие типы атак. Кроме перечисленных основных типов криптоаналитических атак, можно отметить, по крайней мере, еще два типа. 5. Криптоаналитическая атака с использованием выбранного шифртекста Криптоаналитик может выбирать для расшифрования различные шифртексты С1, С2, …, Сi и имеет доступ к расшифрованным открытым текстам М1, М2, …, Мi. Например, криптоаналитик получил доступ к защищенному от несанкционированного вскрытия блоку, который выполняет автоматическое расшифрование. Работа криптоаналитика заключается в нахождении ключа. Этот тип криптоанализа представляет особый интерес для раскрытия алгоритмов с открытым ключом. 6. Криптоаналитическая атака методом полного перебора всех возможных ключей Эта атака предполагает использование криптоаналитиком известного шифртекста и осуществляется посредством полного перебора всех возможных ключей с проверкой, является ли осмысленным получающийся открытый текст. Такой подход требует привлечения предельных вычислительных ресурсов и иногда называется силовой атакой. Существуют и другие, менее распространенные, криптоаналитические атаки. 9.2. Основные виды шифрования Б 15 ольшинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования-расшифрования. В соответствии со стандартом ГОСТ 28147-89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования. Ключ – это конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор только одного варианта из всех возможных для данного алгоритма /1/. Основной характеристикой шифра является криптостойкость, которая определяет его стойкость к раскрытию методами криптоанализа. Обычно эта характеристика определяется интервалом времени, необходимым для раскрытия шифра. К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:
В той или иной мере этим требованиям отвечают:
Ш 16 ифрование перестановкой заключается в том, что символы шифруемого текста переставляются по определенному правилу в пределах некоторого блока этого текста. При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра. Шифрование заменой (подстановкой) заключается в том, что символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены. Шифрование гаммированием заключается в том, что символы шифруемого текста складываются с символами некоторой случайной последовательности, именуемой гаммой шифра. Стойкость шифрования определяется в основном длиной (периодом) неповторяющейся части гаммы шифра. Поскольку с помощью ЭВМ можно генерировать практически бесконечную гамму шифра, то данный способ является одним из основных для шифрования информации в автоматизированных системах. Шифрование аналитическим преобразованием заключается в том, что шифруемый текст преобразуется по некоторому аналитическому правилу (формуле). Например, можно использовать правило умножения вектора на матрицу, причем умножаемая матрица является ключом шифрования (поэтому ее размер и содержание должны храниться в секрете), а символами умножаемого вектора последовательно служат символы шифруемого текста. Другим примером может служить использование так называемых однонаправленных функций для построения криптосистем с открытым ключом. П 17 о мнению К. Шеннона /5/, в практических шифрах необходимо использовать два основных общих принципа: рассеивание и перемешивание. Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста. Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе. Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, т.е. такого шифра, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание. В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановке просто перемешивают символы открытого текста, причем конкретный вид перемешивания определяется секретным ключом. При подстановке каждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно длиной 64 бита. В принципе каждый блок может принимать 264 значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 264 1019 "символов". П 18 ри многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить очень стойкий шифр с хорошим рассеиванием и перемешиванием. Рассмотренные ниже криптоалгоритмы DES, IDEA и отечественный стандарт шифрования данных построен в полном соответствии с указанной методологией. 9.3. Отечественный стандарт шифрования данных В нашей стране установлен единый алгоритм криптографического преобразования данных для систем обработки информации в сетях ЭВМ, отдельных вычислительных комплексах и ЭВМ, который определяется ГОСТ 28147-89 /1/. Стандартобязателен для организаций, предприятий и учреждений, применяющих криптографическую защиту данных, хранимых и передаваемых в сетях ЭВМ, в отдельных вычислительных комплексах и ЭВМ. Этот алгоритм криптографического преобразования данных предназначен для аппаратной и программной реализации, удовлетворяет криптографическим требованиям и не накладывает ограничений на степень секретности защищаемой информации. Алгоритм шифрования данных представляет собой 64-битовый блочный алгоритм с 256-битовымключом. При описании алгоритма используются следующие обозначения: L и R – последовательности битов; LR – конкатенация последовательностей L и R, в которой биты последовательности R следуют за битами последовательности L; – операция побитового сложения по модулю 2; ⊞ – операция сложения по модулю 232 двух 32-разрядных двоичных чисел; ⊞ 19 ´– операция сложения двух 32-разрядных чисел по модулю 232 –1. Два целых числа a, b, где 0 a, b 232 –1, a= (a32a31 ... a2a1), b = (b32, b31, ..., b2, b1), представленные в двоичном виде, т.е. a= a32231 + a31230 +...+ a221 + a1, b = b32231 + b31230 +...+ b221 + b1, суммируются по модулю 232 (операция ⊞) по следующему правилу: a ⊞ b = a + b, если a + b < 232, a ⊞ b = a + b – 232, если a + b 232. Правила суммирования чисел по модулю 232 – 1: a ⊞´ b = a + b, если a + b < 232– 1, a ⊞´ b = a + b – (232 – 1), если a + b 232 – 1. Алгоритм предусматривает четыре режима работы:
Режим простой замены Для реализации алгоритма шифрования данных в режиме простой замены используетсятолько часть блоков общей криптосистемы (рис.1.4). Обозначения на схеме: N1, N2 – 32-разрядные накопители; СМ1 – 32-разрядный сумматор по модулю 232 (⊞); СМ2 – 32-разрядный сумматор по модулю 2 (); R – 32-разрядный регистр циклического сдвига; КЗУ – ключевое запоминающее устройство на 256 бит, состоящее из восьми 32-разрядных накопителей Х0, Х1, Х2, ..., Х7; S – блок подстановки, состоящий из восьми узлов замены (S-блоков замены) S1, S2, S3, ..., S7, S8. 20 9.3.1. Зашифрование открытых данных в режиме простой замены Открытые данные, подлежащие зашифрованию, разбивают на 64-разрядные блоки Т0. Процедура зашифрования 64-разрядного блока Т0 в режиме простой замены включает 32 цикла (j = 1…32). В ключевое запоминающее устройство вводят 256 бит ключа К в виде восьми 32-разрядных подключей (чисел) Кi: К=К7К6К5К4К3К2К1К0. Последовательность битов блока Т0=(a1(0), a2(0), ..., a31(0), a32(0), b1(0), b2(0),..., b31(0), b32(0)) разбивают на две последовательности по 32 бита: b(0) a(0), где b(0) – левые или старшие биты, a(0) – правые или младшие биты. Р  21 исунок1. 4- Схема реализации режима простой замены Эти последовательности вводят в накопители N1 и N2 перед началом первого цикла зашифрования. В результате начальное заполнение накопителя N1 a (0) = (a32(0), a31(0), ..., a2(0), a1(0)), 32, 31, ... 2, 1 номер разряда N1 начальное заполнение накопителя N2 b(0) = (b32(0), b31(0), ..., b2(0), b1(0)). 32, 31, ... 2, 1 номер разряда N2 Первый цикл (j=1) процедуры зашифрования 64-разрядного блока открытых данных можно описать уравнениями: 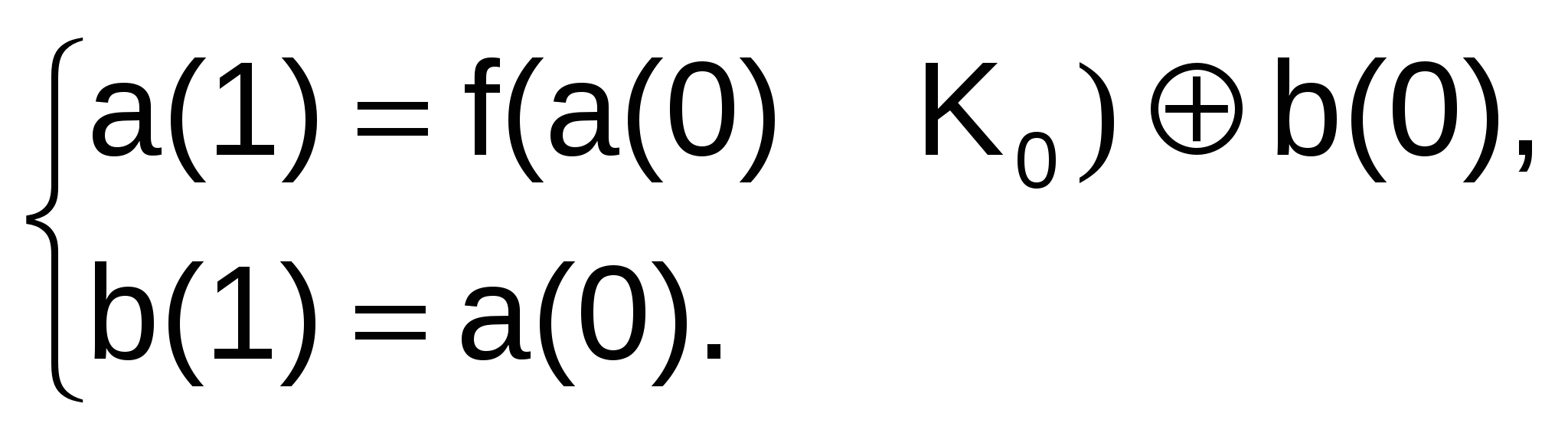  Здесь a(1) – заполнение N1 после 1-го цикла зашифровaния; b(1) – заполнение N2 после 1-го цикла зашифрования; f – функция шифрования. Аргументом функции f является сумма по модулю 232 числа a(0) (начального заполнения накопителя N1) и числа К0 – подключа, считываемого из накопителя Х0 КЗУ. Каждое из этих чисел равно 32 битам. Функция f включает две операции над полученной 32-разрядной суммой (a(0) ⊞ К0). П 22 ерваяоперация называется подстановкой (заменой) и выполняется блокомподстановкиS. Блок подстановки S состоит из восьми узлов замены (S-блоков замены) S1,S2,...,S8 с памятью 64 бит каждый. Поступающий из СМ1 на блок подстановки S 32-разрядный вектор разбивают на восемь последовательно идущих 4-разрядных векторов, каждый из которых преобразуется в четырехразрядный вектор соответствующим узлом замены. Каждый узел замены можно представить в виде таблицы-перестановки шестнадцати четырехразрядных двоичных чисел в диапазоне 0000…1111. Входной вектор указывает адрес строки в таблице, а число в этой строке является выходным вектором. Затем четырехразрядные выходные векторы последовательно объединяют в 32-разрядный вектор. Узлы замены (таблицы-перестановки) представляют собой ключевые элементы, которые являются общими для сети ЭВМ и редко изменяются. Эти узлы замены должны сохраняться в секрете. Втораяоперация – циклический сдвиг влево (на 11 разрядов) 32-разрядного вектора, полученного с выхода блока подстановки S. Циклический сдвиг выполняется регистром сдвига R. Далее результат работы функции шифрования f суммируют поразрядно по модулю 2 в сумматоре СМ2 с 32-разрядным начальным заполнением b(0) накопителя N2. Затем полученный на выходе СМ2 результат (значение a(1)) записывают в накопитель N1, а старое значение N1 (значение a(0)) переписывают в накопитель N2 (значение b(1) = a(0)). Первый цикл завершен. Последующие циклы осуществляются аналогично, при этом во втором цикле из КЗУ считывают заполнение Х1 – подключ К1, в третьем цикле – подключ К2 и т.д., в восьмом цикле – подключ К7. В циклах с 9-го по 16-й, а также в циклах с 17-го по 24-й подключи из КЗУ считываются в том же порядке: К0, К1, К2,...,К6, К7. В последних восьми циклах с 25-го по 32-й порядок считывания подключей из КЗУ обратный: К7, К6, ..., К2, К1, К0. Таким образом, при зашифровании в 32 циклах осуществляется следующий порядок выборки из КЗУ подключей: К0, К1, К2, К3, К4, К5, К6, К7, К0, К1, К2, К3, К4, К5, К6, К7, К0, К1, К2, К3, К4, К5, К6, К7, К7, К6, К5, К4, К3, К2, К1, К0. В 23 32-м цикле результат из сумматора СМ2 вводится в накопитель N2, а в накопителе N1 сохраняется прежнее заполнение. Полученные после 32-го цикла зашифрования заполнения накопителей N1 и N2 являются блоком зашифрованных данных Тш, соответствующим блоку открытых данных Т0. Уравнения зашифрования в режиме простой замены имеют вид:   при j=1…24, при j=1…24,  при j=25…31, при j=25…31,  при j=32, при j=32,где a(j) = (a32(j), a31(j), ..., a1(j)) – заполнение N1 после j-го цикла зашифрования; b(j) = (b32(j), b31(j), ..., b1(j)) – заполнение N2 после j-го цикла зашифрования, j=1…32. Блок зашифрованных данных Тш (64 разряда) выводится из накопителей N1, N2 в следующем порядке: из разрядов 1…32 накопителя N1, затем из разрядов 1…32 накопителя N2, т.е. начиная с младших разрядов: Тш = (a1(32), a2(32), ..., a32(32), b1(32), b2(32), ..., b32(32)). Остальные блоки открытых данных зашифровываются в режиме простой замены аналогично. 9.3.2.Расшифрование в режиме простой замены Криптосхема, реализующая алгоритм расшифрования в режиме простой замены, имеет тот же вид, что и при зашифровании ( рис. 4). В КЗУ вводят 256 бит ключа, на котором осуществлялось зашифрование. Зашифрованные данные, подлежащие расшифрованию, разбиты на блоки Тш по 64 бита в каждом. Ввод любого блока Тш = (a1(32), a2(32), ..., a32(32), b1(32), b2(32), ..., b32(32)) в 24 накопители N1 и N2 производят так, чтобы начальное значение накопителя N1 имело вид (a32(32), a31(32), ..., a2(32), a1(32)), 32, 31, ..., 2, 1 номер разряда N1 а начальное заполнение накопителя N2 – вид (b32(32), b31(32), ..., b2(32), b1(32)). 32, 31, ..., 2, 1 номер разряда N2 Расшифрование осуществляется по тому же алгоритму, что и зашифрование, с тем изменением, что заполнения накопителей X0, Х1, ..., Х7 считываются из КЗУ в циклах расшифрования в следующем порядке: К0, К1, К2, К3, К4, К5, К6, К7, К7, К6, К5, К4, К3, К2, К1, К0, К7, К6, К5, К4, К3, К2, К1, К0, К7, К6, К5, К4, К3, К2, К1, К0. Уравнения расшифрования имеют вид: 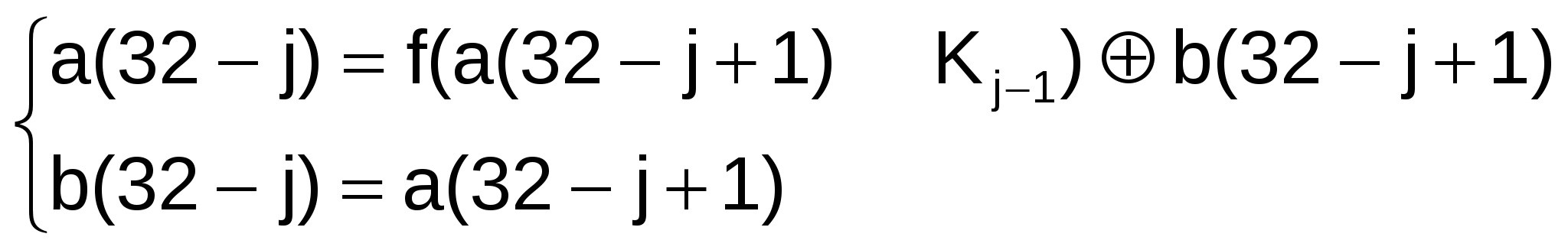  при j=1…8; при j=1…8;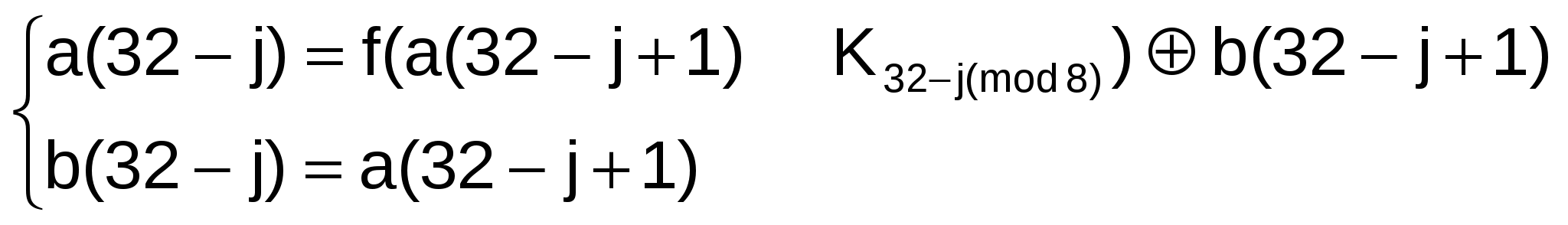  при j=9…31; при j=9…31;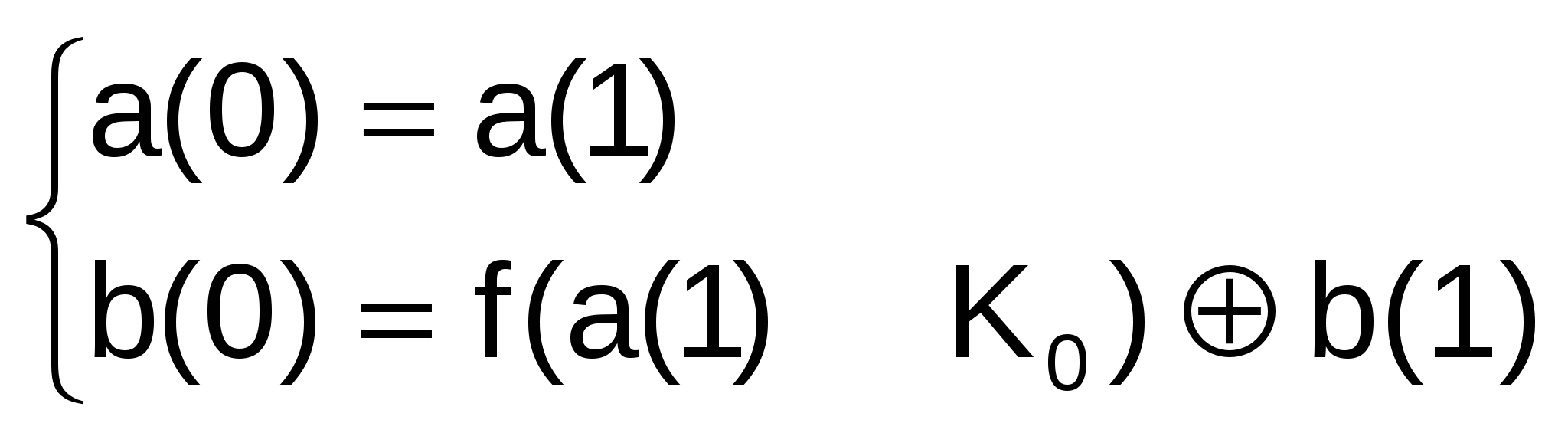  при j=32. при j=32.Полученные после 32 циклов работы заполнения накопителей N1 и N2 образуют блок открытых данных Т0 = (a1(0), a2(0), ..., a32(0), b1(0), b2(0),..., b32(0)), соответствующий блоку зашифрованных данных Тш. При этом состояние накопителя N1 (a32(0), a31(0), ..., a2(0), a1(0)), 32, 31, ..., 2, 1 номер разряда N1 состояние накопителя N2 (b32(0), b31(0), ..., b2(0), b1(0)). 32, 31, ..., 2, 1 номер разряда N2 Аналогично расшифровываются остальные блоки зашифрованных данных. Е 25 сли алгоритм зашифрования в режиме простой замены 64-битового блока Т0 обозначить через А, то А(Т0) = А(a (0), b(0)) = (a (32), b(32))=Тш. Следует иметь в виду, что режим простой замены допустимо использовать для шифрования данных только в ограниченных случаях – при выработке ключа и зашифровании его с обеспечением имитозащиты для передачи по каналам связи или для хранения в памяти ЭВМ. |
