В.И. Берник, О.Н. Пирютко
Методические рекомендации для учителей
Изучение темы «Элементы комбинаторики и бином Ньютона»
1. Различные подходы к изложению элементов комбинаторики учащимся учреждений общего среднего образования
Необходимость рассмотрения различных содержательных, методических, технологических подходов к изучению темы «Элементы комбинаторики и бином Ньютона» связана прежде всего с закономерностями формирования знаний. Первой и основной методической закономерностью является организация подвижности знаний, на основании которых формируются новые знания. Один из традиционных подходов к изучению правил комбинаторики – теоретико-множественный. В этом случае знания, на основании которых формируются новые знания, – это знание элементов теории множеств. Для усвоения новой темы учащимися необходимы знания и умения применять следующие понятия теории множеств: множество, элемент множества, подмножества, пересечение, объединение множеств, пустое множество, упорядоченные множества; свойства множеств. Такой подход осуществлялся в школьном курсе математики в 1970-е годы, в период так называемой колмогоровской реформы школьной математики. На сегодняшний день в школьном курсе математики теоретико-множественный подход отсутствует. Поэтому изучение элементов комбинаторики требует иного подхода.
Проиллюстрируем возможности изучения этого нового раздела, заложенного в переходной программе Х класса для изучения математики на повышенном уровне. При этом укажем на взаимосвязь этих подходов, возможности методики и технологии реализации общих обучающих компонентов как в теории, так и в практике решения задач. Выполним сравнительный анализ формирования теоретических знаний на примере изучения раздела «Перестановки без повторений».
Перестановки без повторений
|
|
|
|
Тридцать три буквы русского алфавита принято располагать в таком порядке: А, Б, В, Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.
При этом порядке расположения букв, буква А является первой, Б – второй, В – третьей и т.д. вплоть до тридцать третьей буквы Я. Мы имеем дело с упорядоченным множеством.
Определение 1. Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число (номер элемента) от 1 до n, где n – число элементов множества, так что различным элементам соответствуют различные числа.
Очевидно, что каждое множество, содержащее более одного элемента, можно упорядочить не единственным способом.
Определение 2. Упорядоченные множества, которые отличаются лишь порядком элементов (то есть могут быть получены из того же самого множества), называются перестановками этого множества.
Множество из одного элемента можно упорядочить одним способом: единственный элемент множества приходится считать первым. Возьмем множество из двух элементов, для примера: из двух букв А и Б. Очевидно, что их можно расположить по порядку двумя способами:
АБ или БА.
Три буквы А, Б, В можно расположить по порядку шестью способами:
АБВ, АВБ, БАВ, БВА, ВАБ, ВБА.
Число перестановок из n-элементов обозначают  . Мы нашли, что . Мы нашли, что 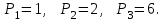
Докажем, что вообще  (число перестановок из n-элементов) равно произведению первых n-натуральных чисел: (число перестановок из n-элементов) равно произведению первых n-натуральных чисел:
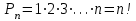
Будем последовательно выбирать элементы данного множества и размещать их в определенном порядке на n-местах. На первое место можно поставить любой из n-элементов. После того как заполнится первое место, на второе место можно поставить любой из оставшихся  элементов. После того как заполнятся первое и второе места, на третье место можно поставить любой из оставшихся элементов. После того как заполнятся первое и второе места, на третье место можно поставить любой из оставшихся 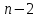 элементов и т. д. По правилу умножения все n-места можно заполнить: элементов и т. д. По правилу умножения все n-места можно заполнить:

способами. Таким образом, 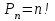 . .
Пример
В пассажирском поезде 14 вагонов. Сколькими способами можно распределить по вагонам 14 проводников, если за каждым вагоном закрепляется один проводник?
Решение
Ясно, что в этом случае каждый способ отличается от других только порядком расположения элементов, а значит, число способов равно числу перестановок из 14 элементов. 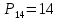 ! !
|
Определение
Перестановками из n различных элементов называются соединения (наборы), каждое (-ый) из которых содержит эти n-элементы, взятые в определенном порядке.
Замечание 1. Перестановкой из n-элементов можно считать установленный в конечном множестве порядок.
Обозначение
Число всех пeрестановок из n-элементов обозначается Pn (от фр. реrmutation – «перестановка»).
Различные перестановки отличаются друг от друга только порядком расположения элементов.
Выведем формулу для подсчета числа перестановок из n-элементов.
Вывод формулы
Пусть имеется n различных элементов, которые нужно распределить по n-местам. Выбор первого элемента можно осуществить n-способами (иначе на первое место можно поставить любой из n-элементов). После выбора первого элемента второй элемент можно выбрать (n – 1) способом (на второе место можно поставить любой из оставшихся (n – 1) элемент, третий элемент можно выбрать (n – 2) способами и т.д. Последний элемент – 1 способом.
По правилу произведения n-элементов можно выбрать
n·(n – 1)·(n – 2)·(n – 3)·…·1 способом, то есть число способов равно произведению всех натуральных чисел от 1 до n.
Для такого произведения применяют специальное обозначение n! (читается «эн факториал»).
Например, 2! = 1 · 2, 3! = 1 · 2 · 3, 10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3 628 800.
Таким образом, число перестановок из n-элементов равно Pn = n!
Пример
Сколько различных четырехзначных чисел можно составить из цифр 3, 5, 7, 9 так, чтобы все цифры были различными?
Решение
Так как каждое число будет отличаться от другого только порядком расположения цифр, то количество чисел, составленных из указанных цифр, будет равно числу перестановок из 4 элементов. По формуле числа перестановок из n-элементов получим:
P4 = 4! = 1 · 2 · 3 · 4 = 24.
Иллюстрация (рис. 1)
На рисунке 1 показано, как получить перестановки из четырех различных элементов.
На первое место можно поставить любой из четырех элементов (первый столбик), на второе – любой из оставшихся трех (от каждого выбранного элемента – три стрелки), на третье – любой их оставшихся двух (от каждого второго выбранного элемента – две стрелки), на четвертое – оставшийся один элемент от каждого третьего элемента – одна стрелка).
Всего комбинаций будет P4 = 4 · 3 · 2 · 1 = 24
Р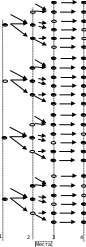 ис. 1 ис. 1
|
Анализ: отметим, что первый подход основан на использовании понятий теории множеств. Изучению комбинаторного понятия «перестановка» предшествует рассмотрение основных понятий теории множеств. Для их первоначального усвоения нужна дополнительная система упражнений, а для применения в различных измененных условиях – включение этих понятий в систему интегрированных упражнений.
Второй подход не использует понятия теории множеств. Опора на личный практический опыт, привычные для учащихся представления о наборе, комбинации, порядке расположения объектов позволяют уменьшить количество новых терминов, связанных с ними новых понятий, рассматривать модели конструирования количества рассматриваемых наборов. Первый подход может быть использован на факультативных занятиях, второй – на уроках математики. Прослеживается связь между этими двумя подходами: во втором подходе в замечании 1 используются на интуитивном уровне понятия множества, элемента множества. В первом подходе активно используется понятие числа комбинаций и способа выбора, используемого во втором подходе.
Второй подход реализован в методическом пособии В. И. Берника, О. Н. Пирютко «Элементы комбинаторики и бином Ньютона» [1].
Структура пособия представлена следующими разделами по каждой теме:
краткая теория с выводами основных формул и их иллюстрациями;
примеры применения формул с решениями;
контрольные вопросы, содержащие проверочные задания на знание теории и применения ее для решения задач с ответами;
разноуровневые тесты (пять уровней) с ответами для проверки и коррекции знаний;
разноуровневые тесты (пять уровней) с ответами для самостоятельной работы;
дополнительные материалы для индивидуальной работы;
разноуровневые тесты (пять уровней) с ответами для самостоятельной работы и дополнительные задачи;
исторические сведения.
2. Анализ методических приемов решения задач
Комбинаторные задачи на применение правил умножения, сложения, вычисления числа перестановок, размещений, сочетаний требуют особых приемов, формирующих комбинаторное мышление учащихся. Комбинаторные задачи практически обеспечивают формирование ключевых образовательных компетенций: уметь выполнять анализ проблемы (получать, организовывать и обрабатывать информацию, наблюдать, использовать эксперимент с помощью программных средств, искать примеры или контрпримеры, упрощать или конкретизировать ситуацию; предложить гипотезу, подтвердить правильный подход или принять новый); моделировать (перевести на математический язык реальную ситуацию); представлять (выбирать рамки (цифровые, алгебраические, геометрические), подходящие для работы с проблемой и представлением математического объекта, выполнять переключение из одного режима представления к другому); вычислять (выполнять расчет вручную или с помощью инструментов (калькулятор, программное обеспечение), реализовывать простые алгоритмы, выполнять упражнение на интеллектуальные вычисления: организовать различные этапы сложного расчета, выбирать преобразования, выполнять упрощения, проверять расчеты).
Задачи так называемого первого уровня (в шкале оценок 1–3 уровень) требуют умения выполнять два вида познавательных действий: классифицировать объекты по признакам, соответствующим определениям основных видов комбинаций, и конкретизировать применение правила в задаче. Обучение распознаванию вида комбинации целесообразно через организацию алгоритмической деятельности.
Алгоритм выбора вида соединения

Проиллюстрируем использование этого алгоритма, позволяющего учащимися отнести задачу к определенному классу и реализовать математическую модель, соответствующую выбору.
Задача 1
Сколько различных четырехзначных чисел можно составить из цифр 1, 5, 8, 9 так, чтобы все цифры участвовали в записи?
Решение: в соответствии с алгоритмом, проверим, все ли элементы участвуют в наборе. Так как всего цифр четыре и все они используются в записи числа, то применим формулу числа перестановок из n-элементов и получим:
P4 = 4! = 1 · 2 · 3 · 4 = 24.
Задача 2
У филателиста 9 новых марок. Сколькими способами он может наклеить четыре из них на 4 пронумерованных места?
Решение: в соответствии с алгоритмом проверим, все ли элементы участвуют в наборе. Так как всего 9 марок, а выбрать нужно 4, то в наборе марок используются не все элементы. Так как места расположения марок пронумерованы, то порядок расположения элементов в наборе имеет место. Следовательно, для ответа на вопрос задачи применяем формулу числа размещений из девяти элементов по четыре: 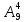 = 9 · 8 ∙ 7 ∙ 6 = 3024. = 9 · 8 ∙ 7 ∙ 6 = 3024.
Другой класс комбинаторных задач связан с трудностями выбора типа комбинации алгоритмически. Необходимы новые приемы, такие как применение правила «решета», составление математической модели комбинации, позволяющей представить наборы, удовлетворяющие условию. Задачи такого типа достаточно сложны, предлагаются для заданий 4–5 уровней. Проиллюстрируем указанные методические приемы решения комбинаторных задач на примерах.
Задача 3
Сколько различных нечетных четырехзначных чисел можно составить из цифр 1, 3, 7, 8 так, чтобы все цифры участвовали в записи?
Решение: подсчитаем сначала количество всех чисел, которые можно составить из цифр 1, 3, 7, 8. Их число будет равно P4 , а затем из общего числа вычтем количество четных чисел («просеиваем» ненужные), их будет столько, сколько различных перестановок можно сделать из трех нечетных цифр из имеющихся (цифра «8» помещается на последнее место).
P4 – P3 = 24 – 6 = 18.
Задача 4
Сколькими различными способами можно разложить 12 различных конфет по трем коробкам?
Решение: используем прием составления математической модели комбинации, по которой можно увидеть ожидаемый результат.
Такой моделью будет набор из двенадцати компонентов, составленный из трех цифр (или других символов, соответствующих коробкам).
Например, наборы 113332221133; 111111112222 вполне определенно объясняют, как располагаются конфеты в коробках. Первый набор показывает, что первую, вторую, девятую и десятую конфету поместили в первую коробку; шестую седьмую, восьмую – во вторую, остальные – в третью. Второй набор указывает, что первые восемь конфет – в первой коробке, последние четыре – во второй, а в третьей коробке нет конфет. Очевидно, что эти наборы иллюстрируют размещения из трех элементов с повторениями. Число таких наборов вычисляется по формуле 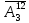 = =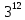 . .
3. Поурочное планирование изучения темы «Элементы комбинаторики и Бином Ньютона» с использованием пособия [1]
На изучение этой темы в соответствии с программой отводится 10 часов.
Тема урока № 1
|
Общие правила комбинаторики (Гл. 1 п. 1)
|
Цель урока
|
Сформировать представление о комбинаторике как разделе математики, в котором изучаются способы подсчета всевозможных комбинаций из некоторых элементов (объектов), составленных по определенным правилам. Сформировать правила суммы и произведения. Научить применять эти правила для решения двух видов комбинаторных задач
|
Ожидаемые результаты
|
Учащиеся будут иметь представление о комбинаторике; знать правила произведения и суммы и уметь их применять для решения комбинаторных задач (в несильно измененных условиях)
|
Содержание теории
|
Рассмотреть правило произведения, обобщенное правило произведения, правило суммы, обобщенное правило суммы
|
Содержание практики
|
Разбор примеров применения правил из текста пособия. Решение заданий из раздела «Контрольные вопросы»: рассмотреть вопросы № 1, 2, 3, 4, 6, 7, 9, 10
|
Домашнее задание
|
Задания из раздела «Контрольные вопросы» № 5, 8, 11, 12
|
Тема урока № 2
|
Перестановки без повторений (Гл. 1 п. 2)
|
Цель урока
|
Сформировать представление о перестановках, формуле подсчета числа перестановок без повторений. Сформировать правило подсчета числа перестановок из n-элементов без повторений
|
Ожидаемые результаты
|
Учащиеся будут знать термин и правильно применять понятие «перестановка», применять формулу для подсчета числа перестановок из n-элементов для решения комбинаторных задач на применение этих правил (в несильно измененных условиях)
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов первого раздела; можно предложить учащимся одно, два или три задания в зависимости от уровня подготовленности учащихся
|
Содержание теории
|
Рассмотреть определение понятия перестановки, вывод формулы числа перестановок. Понятие факториала
|
Содержание практики
|
Разбор примеров применения правила подсчета числа перестановок из текста пособия. Решение заданий из раздела «Контрольные вопросы»: рассмотреть вопросы № 1, 2, 4, 6, 7, 9, 10, 13
|
Домашнее задание
|
Задания из раздела «Контрольные вопросы» № 3, 5, 8, 11, 12, 14
|
Тема урока № 3
|
Размещения без повторений (Гл. 1 п. 3)
|
Цель урока
|
Сформировать представление о размещении из n-элементов по m, формуле подсчета числа размещений без повторений. Сформировать правило подсчета числа размещений из n-элементов по m без повторений
|
Ожидаемые результаты
|
Учащиеся будут знать термин и правильно применять понятие «размещение», применять формулу для подсчета числа размещений из n-элементов по m для решения комбинаторных задач на применение этих правил (в несильно измененных условиях)
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов второго раздела, можно предложить учащимся одно, два или три задания в зависимости от уровня подготовленности учащихся
|
Содержание теории
|
Рассмотреть определение понятия размещений, вывод формулы числа размещений из n-элементов по m.
|
Содержание практики
|
Разбор примеров применения правила подсчета числа размещений из текста пособия. Решение заданий из раздела «Контрольные вопросы». Рассмотреть вопросы № 1, 2, 4, 6, 7, 9, 10, 12
|
Домашнее задание
|
Задания из раздела «Контрольные вопросы» № 3, 5, 8, 11, 13, 14
|
Тема урока № 4
|
Сочетания без повторений (Гл. 1 п. 4)
|
Цель урока
|
Сформировать представление о сочетаниях, формуле подсчета числа сочетаний без повторений. Сформировать правила подсчета числа сочетаний из n-элементов по m без повторений
|
Ожидаемые результаты
|
Учащиеся будут знать термин и правильно применять понятие «сочетания», применять формулу для подсчета числа сочетаний из n-элементов по m для решения комбинаторных задач на применение этих правил (в несильно измененных условиях)
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов третьего раздела, можно предложить учащимся одно, два или три задания в зависимости от уровня подготовленности учащихся
|
Содержание теории
|
Рассмотреть определение понятия сочетаний, вывод формулы числа сочетаний из n-элементов по m, свойства числа сочетаний
|
Содержание практики
|
Разбор примеров применения правила подсчета числа сочетаний и свойств сочетаний из текста пособия. Решение заданий из раздела «Контрольные вопросы». Рассмотреть вопросы № 1, 2, 4, 6, 8, 9, 10, 12
|
Домашнее задание
|
Задания из раздела «Контрольные вопросы» № 1, 3, 5, 9, 11, 13, 15
|
Тема урока № 5
|
Применение правил комбинаторики (Гл. 1 п. 6)
|
Цель урока
|
Формирование навыков применения алгоритма для выбора вида комбинаций, правил подсчета числа перестановок, размещений, сочетаний без повторений, правил произведения и суммы
|
Ожидаемые результаты
|
Учащиеся будут уметь применять алгоритм выбора вида комбинаций и применять его при решении задач в различных условиях
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов четвертого раздела; можно предложить учащимся два или три задания каждого уровня в зависимости от подготовленности учащихся
|
Содержание теории
|
Рассмотреть алгоритм выбора вида комбинации, примеры его применения
|
Содержание практики
|
Разбор примеров применения алгоритма. Решение заданий из раздела № 6. Решение комбинаторных задач. Можно выполнить задания: 1 уровень № 1, 2 уровень № 3, 3 уровень № 1, 4 уровень № 1, 5 уровень № 1
|
Домашнее задание
|
Задания из раздела «Дополнительные задачи» № 1, 4, 7, 9, 11, 12
|
Тема урока № 6
|
Бином Ньютона (Гл. 2)
|
Цель урока
|
Сформировать навыки применения формулы для разложения бинома Ньютона: для представления степени в виде суммы и суммы одночленов в виде степени бинома
|
Ожидаемые результаты
|
Учащиеся будут уметь применять формулу бинома Ньютона с использованием треугольника Паскаля и с помощью формулы числа сочетаний и свойств 1-5 биномиальных коэффициентов
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов раздела «Тесты для самостоятельной работы»; можно использовать одно, два или три задания каждого уровня в зависимости от подготовленности учащихся
|
Содержание теории
|
Рассмотреть формулу бинома Ньютона, вывод формулы. Свойства 1-5
|
Содержание практики
|
Можно рассмотреть разбор примеров применения формулы и свойств 1-5 и контрольные вопросы 1-3-5-9
|
Домашнее задание
|
Задания из раздела «Контрольные вопросы» 2-4-6-11
|
Тема урока № 7
| Основные следствия из формулы бинома Ньютона
|
Цель урока
|
Сформировать навыки применения следствий из формулы для разложения бинома Ньютона
|
Ожидаемые результаты
|
Учащиеся будут уметь применять следствия 6-8 из формулы бинома Ньютона для вычисления коэффициентов, суммы коэффициентов, определения к-го члена бинома
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов
|
Содержание теории
|
Рассмотреть следствия 6-8 формулы бинома Ньютона, вывод формулы. Свойства 6-8
|
Содержание практики
|
Можно рассмотреть разбор примеров применения свойств 6–8 и контрольные вопросы 7, 12, 13, 15
|
Домашнее задание
|
Свойства 1-8. Задания из раздела «Контрольные вопросы» 8, 14
|
Тема урока № 8
| Основные следствия из формулы бинома Ньютона
|
Цель урока
|
Сформировать навыки применения следствий из формулы для разложения n-й степени бинома Ньютона
|
Ожидаемые результаты
|
Учащиеся будут уметь применять следствия из формулы бинома Ньютона для вычисления коэффициентов, суммы коэффициентов, определения к-го члена бинома
|
Диагностика
|
Выполнить диагностическую работу с использованием тестов: 1 или 2 задания из разноуровневых тестов
|
Содержание теории
|
Рассмотреть примеры применения основных следствий из формулы бинома Ньютона для решения задач повышенной сложности: задачи уровня 5
|
Содержание практики
|
Рассмотреть задачи из тестов для самостоятельной работы для индивидуальной и групповой работы
|
Домашнее задание
| Повторить свойства 1-8. Задания из раздела «Тесты для самостоятельной работы» |
Тема урока № 9
| Обобщение и систематизация знаний по теме «Элементы комбинаторики и Бином Ньютона» |
Цель урока
|
Обобщить и систематизировать основные приемы решения задач по теме «Элементы комбинаторики и бином Ньютона»
|
Ожидаемые результаты
|
Учащиеся будут уметь применять правила подсчета числа различных комбинаций. Решать задачи на применение формулы бинома Ньютона и следствий из нее
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов для самостоятельной работы
|
Содержание теории
|
В зависимости от уровня подготовленности класса можно рассмотреть формулы подсчета числа перестановок, размещений, сочетаний с повторениями. Второй вариант – решать интегрированные задачи по изученному материалу
|
Содержание практики
|
Можно рассмотреть задачи раздела «Дополнительный материал», задачи из «Контрольных вопросов»
|
Домашнее задание
|
Задания из раздела «Дополнительные задачи» или из раздела «Дополнительный материал»
|
Тема урока № 10
| Обобщение и систематизация знаний по теме «Элементы комбинаторики и бином Ньютона» |
Цель урока
|
Обобщить и систематизировать полученные знания. Решение задач на применение формулы бинома Ньютона
|
Ожидаемые результаты
|
Учащиеся будут уметь применять правила подсчета числа различных комбинаций. Решать задачи на применение формулы бинома Ньютона и следствий из нее
|
Диагностика
|
Выполнить диагностическую работу с использованием разноуровневых тестов для самостоятельной работы
|
Содержание теории
|
Разбор дополнительных приемов решения комбинаторных задач
|
Содержание практики
|
Решение задач из раздела «Тесты для самостоятельной работы»
|
Домашнее задание
|
Индивидуальное задание по материалам разделов «Дополнительный материал», «Тесты для самостоятельной работы»
| |
 Скачать 75.53 Kb.
Скачать 75.53 Kb.
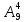 = 9 · 8 ∙ 7 ∙ 6 = 3024.
= 9 · 8 ∙ 7 ∙ 6 = 3024.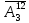 =
=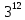 .
.
 . Мы нашли, что
. Мы нашли, что 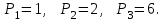
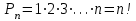
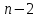 элементов и т. д. По правилу умножения все n-места можно заполнить:
элементов и т. д. По правилу умножения все n-места можно заполнить:
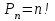 .
.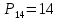 !
! ис. 1
ис. 1