Методические рекомендации и указания

• Название: Методические рекомендации и указания
• Дата: 16.03.2023
• Размер: 0.62 Mb.
• Имя файла: 82487.doc
• Тип: Методические рекомендации; #994608
• страница: 4 из 6

1.3 Диэлектрики

12 Между пластинами плоского конденсатора без воздушных промежутков зажат лист диэлектрика толщиной =1 мм. На конденсатор подано напряжение =200 В. Определить поверхностную плотность заряда на пластинах конденсатора и на диэлектрике . Диэлектрическая проницаемость равна шести.

Решение

Вследствие поляризации диэлектрика при подключенном источнике постоянного напряжения на пластинах конденсатора удерживается дополнительный заряд , так что , где – поверхностная плотность заряда на пластинах конденсатора в отсутствие диэлектрика. Тогда

Кл/м²;

Кл/м².
13 Композиционный термокомпенсированный (т.е. материал с температурным коэффициентом диэлектрической проницаемости равным нулю) керамический материал изготовлен на основе двух диэлектриков с диэлектрическими проницаемостями =40; и = 210^–4 К^–1; = –1,510^–3 К^–1. Предполагая хаотическое распределение компонентов, определить состав керамики и диэлектрическую проницаемость ее.

Решение

Используем формулу Лихтенеккера , где и – объемные концентрации компонентов.

Температурный коэффициент диэлектрической проницаемости композиционного диэлектрика можно вычислить, продифференцировав формулу Лихтенеккера: . Так как материал термокомпенсированный, =0.

Решая систему уравнений



находим 0,882, =0,112.

Из формулы Лихтенеккера, подставляя и , получим =43,4.
14 Две противоположные грани куба с ребром = 10 мм из диэлектрического материала с удельным объемным сопротивлением =10¹⁰ Омм и удельным поверхностным сопротивлением =10¹¹ Ом на квадрат покрыты металлическими электродами. Определить ток, протекающий через эти грани куба при постоянном напряжении =2 кВ.

Решение

Электрический ток протекает как через объем куба, так и по поверхности четырех боковых граней. Поэтому сопротивление между электродами определяется параллельным соединением объемного сопротивления и поверхностных сопротивлений четырех граней. Так как объемное сопротивление вычисляется по формуле , а поверхностное сопротивление определяется как , где – длина, ширина и площадь поперечного сечения образца.

В нашем случае Ом;

10¹¹ Ом.

Полное поверхностное сопротивление , а полное сопротивление между электродами Ом.

Ток между электродами А.
15 В дисковом керамическом конденсаторе емкостью 100 пФ, включенном на переменное напряжение100 В частотой 1МГц, рассеивается мощность Вт. Определить удельные потери в диэлектрике, если его диэлектрическая проницаемость равна 150, электрическая прочность = 10 МВ/м и запас по электрической прочности .

Решение

Удельные потери рассчитываются на объем рабочего диэлектрика конденсатора: , где – площадь обкладки и толщина диэлектрика соответственно. Толщину диэлектрической пленки находим из условия обеспечения электрической прочности: для постоянного напряжения или для переменного.

м.

Площадь обкладок может быть определена из выражения для емкости плоского конденсатора:

м².

Отсюда Вт/м³.
16 На пластину пьезоэлектрического кварца толщиной мм вдоль оси действует механическое напряжение Н/м². Определить разность потенциалов между противоположными плоскостями пластины, если в направлении оси пьезомодуль продольного пьезоэффекта Кл/Н. Диэлектрическая проницаемость кварца равна 4,6.

Решение

В соответствии с уравнением прямого пьезоэффекта . Для плоского однородного диэлектрика при равномерной механической нагрузке заряд на поверхности равен . Разность потенциалов между плоскими гранями определим, воспользовавшись зависимостью между величиной емкости конденсатора, площадью его обкладок и разностью потенциалов на них: , а также ,

В.
17 Конденсатор емкостью 200 пФ, изготовленный из пленки полистирола, заряжен до напряжения 100 В, а затем отключен от источника напряжения. Измерения, проведенные через 5 суток, показали, что на выводах конденсатора сохранилось напряжение 10 В. Пренебрегая поверхностной утечкой, определить сопротивление изоляции конденсатора и удельное объемное сопротивление полистирола. Диэлектрическая проницаемость полистирола равна 2,5.

Решение

Изменение напряжения на выводах конденсатора в процессе саморазряда описывается выражением 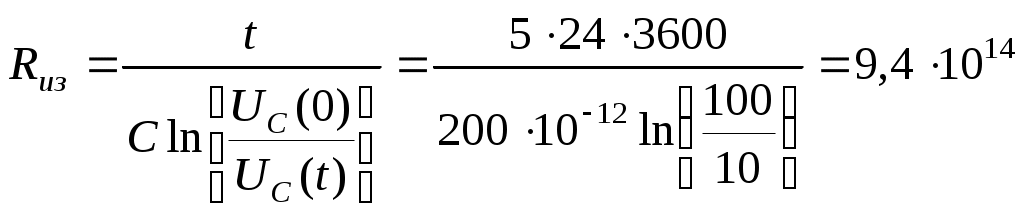, где напряжение, до которого был заряжен конденсатор; – постоянная времени конденсатора. Прологарифмировав выражение, получим . Отсюда Ом.

Так как , то Омм.