|
|
Методические рекомендации и указания
1.1 Проводниковые материалы
1 Известно, что алюминий кристаллизуется в решетке гранецентрированного куба с периодом a=0,4041 нм. Вычислить концентрацию свободных электронов, полагая, что на каждый атом кристаллической решетки приходится три электрона.
Решение
В решетке гранецентрированного куба на одну элементарную ячейку приходится четыре атома. Поэтому число атомов в единице объема:
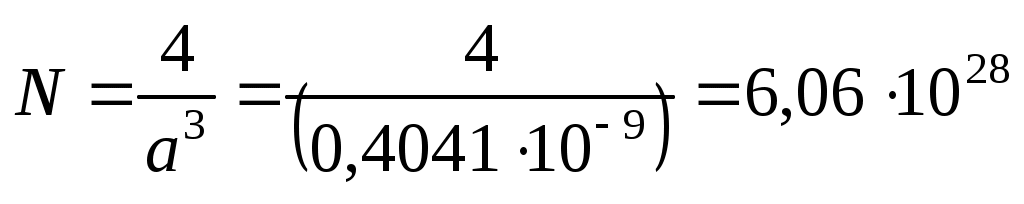 м–3. м–3.
Отсюда концентрация электронов:
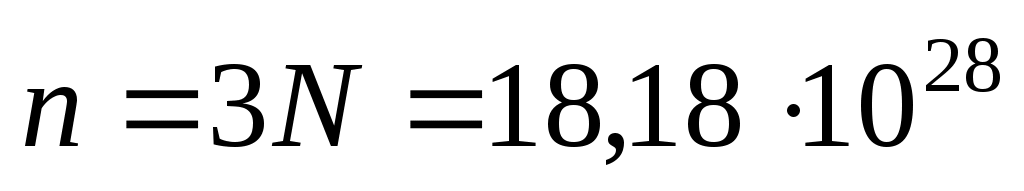 м–3. м–3.
2 Вычислить длину свободного пробега электронов в меди при T=300 К, если ее удельное сопротивление при этой температуре равно 0,017 мкОм/м.
Решение
Согласно представлениям квантовой теории, удельная проводимость металлов 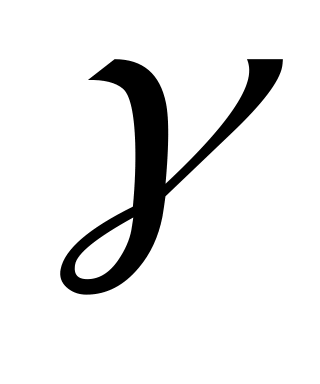 связана с длиной свободного пробега электронов связана с длиной свободного пробега электронов 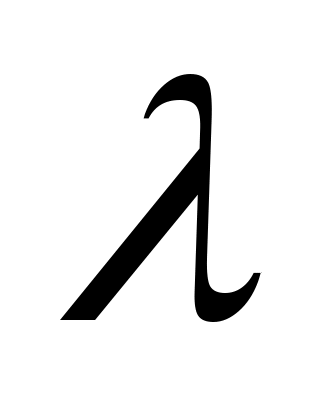 соотношением: соотношением:
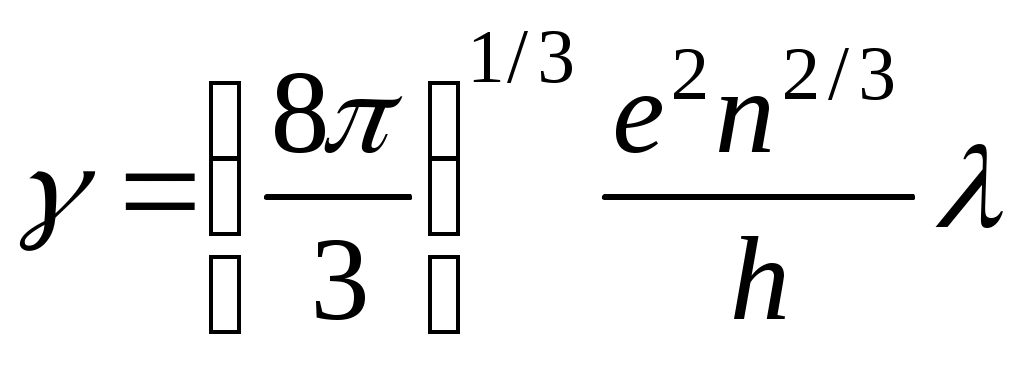 , а по определению , а по определению 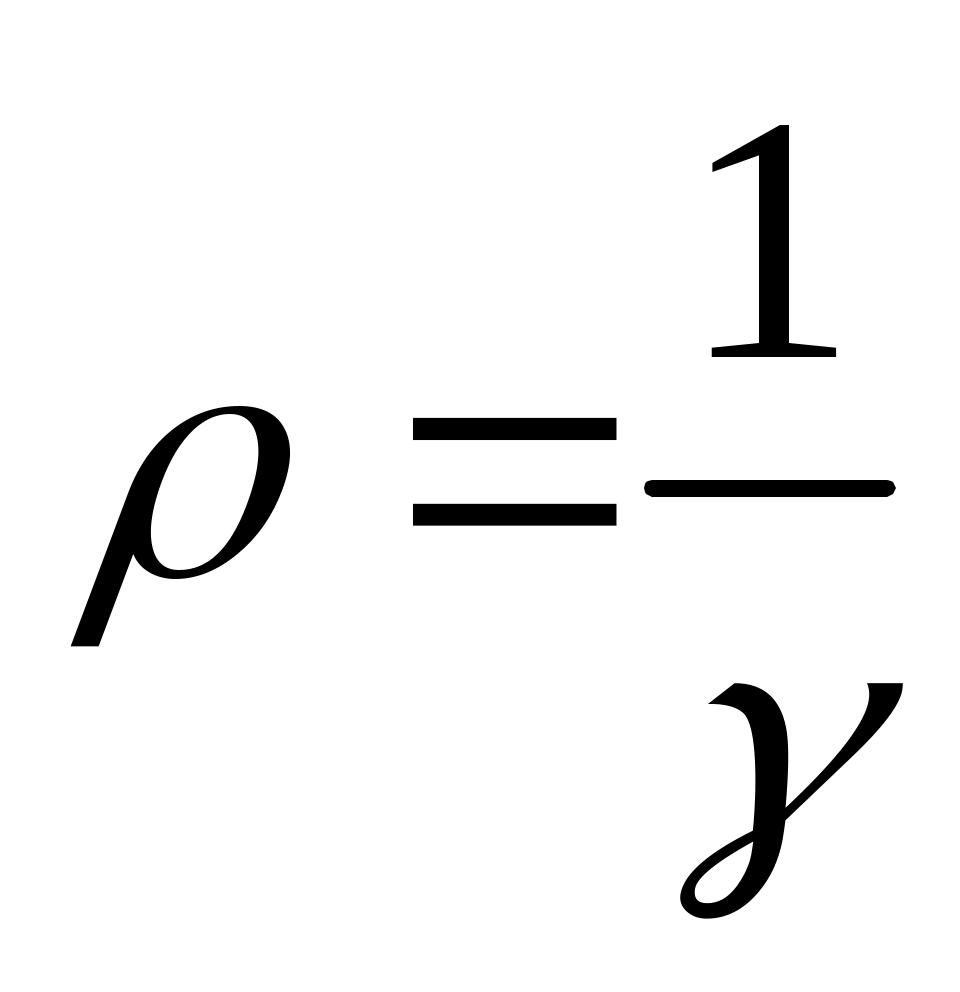 . .
Концентрация свободных электронов в меди равна концентрации атомов:
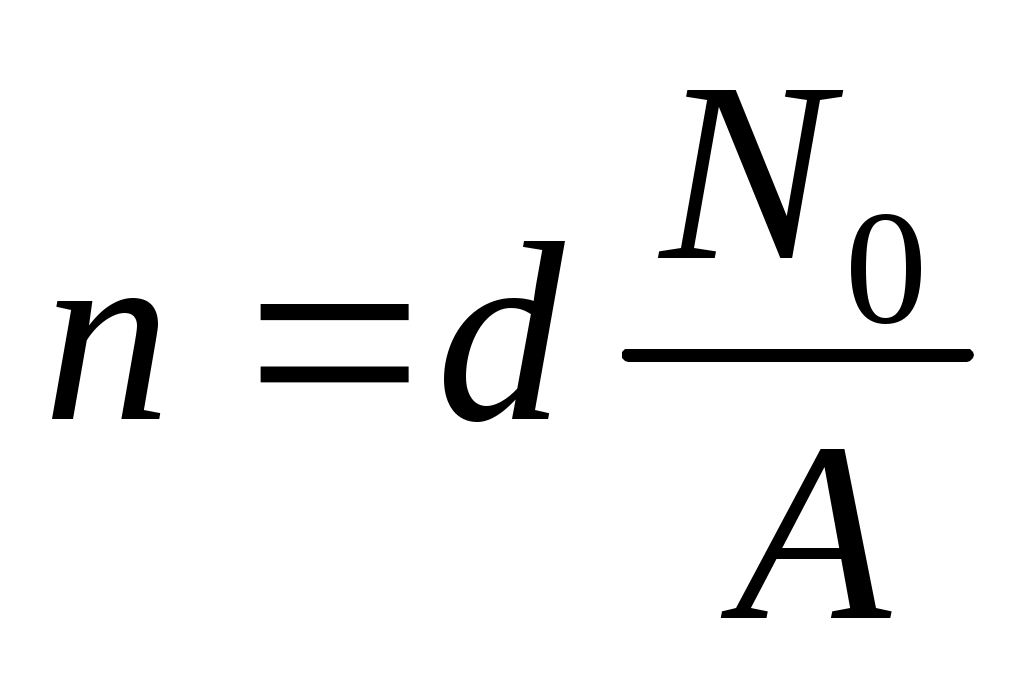 (d – плотность меди, (d – плотность меди, 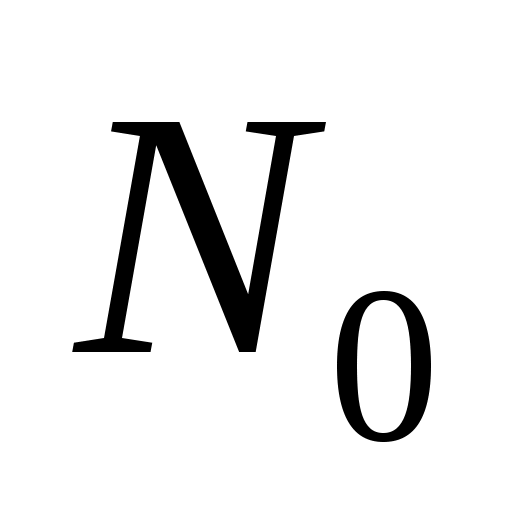 – число Авогадро, А – атомная масса). – число Авогадро, А – атомная масса).
Следовательно 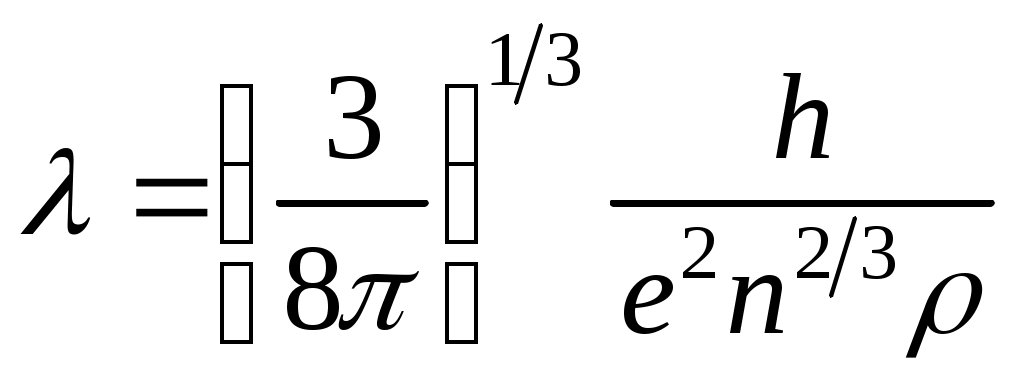 =3,8910–8 м. =3,8910–8 м.

3 Определить, во сколько раз изменится удельная теплопроводность 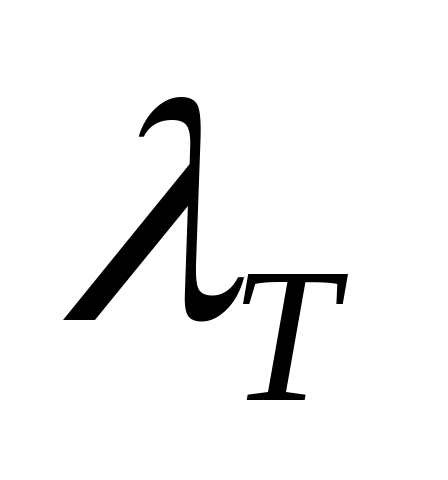 меди при изменении температуры от 20 до 200 оС. меди при изменении температуры от 20 до 200 оС.
Решение
Согласно закону Видемана-Франца, 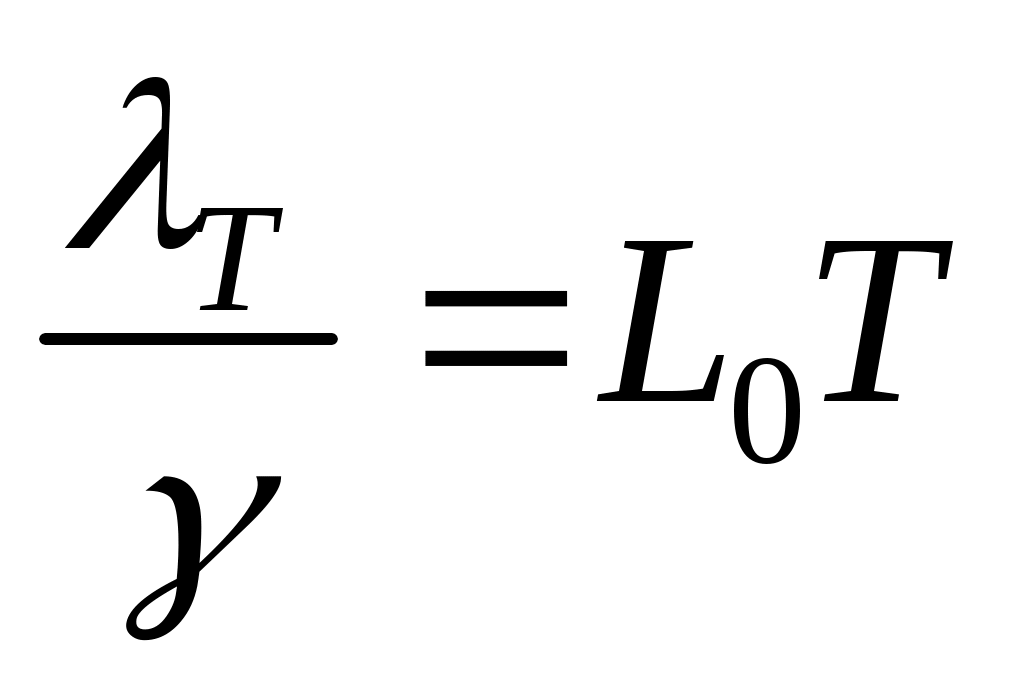 , где , где 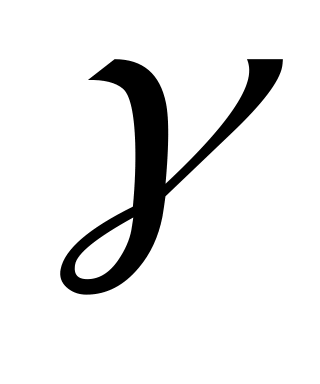 – удельная проводимость; – удельная проводимость; 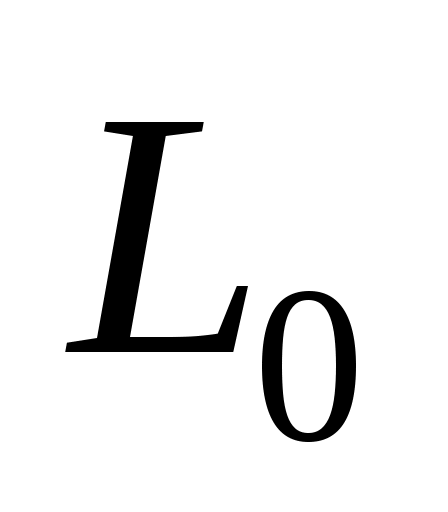 – число Лоренца. Отсюда следует, что – число Лоренца. Отсюда следует, что 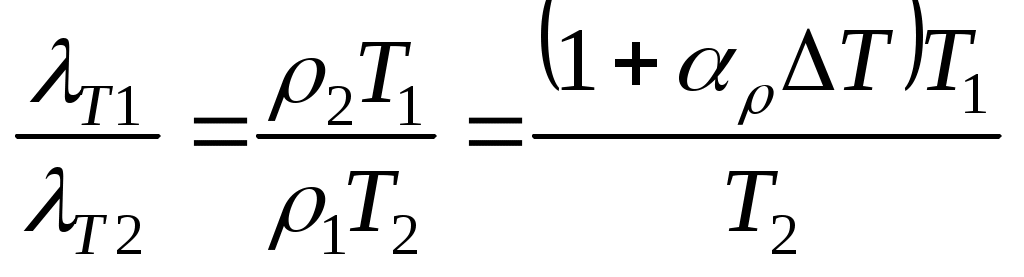 =1,12 ( =1,12 (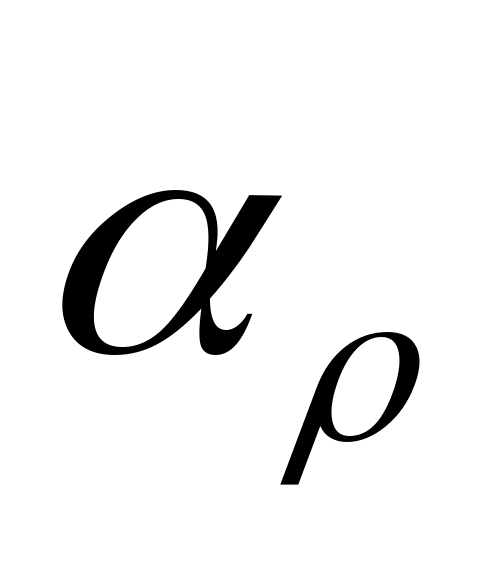 =4,310–3 К–1 для меди). =4,310–3 К–1 для меди).
4 Удельное сопротивление меди, содержащей 0,3 атомных процента олова при температуре 300 К, составляет 0,0258 мкОм м. Определить отношение 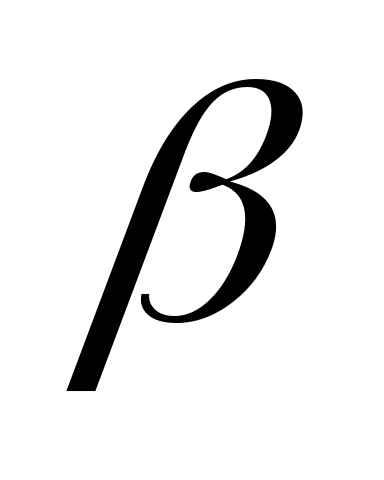 удельных сопротивлений меди при температурах 300 и 4,2 К. удельных сопротивлений меди при температурах 300 и 4,2 К.
Решение
Согласно правилу Маттисена, 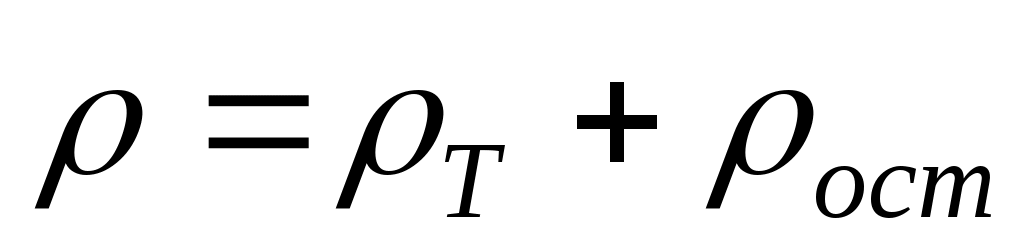 , где , где 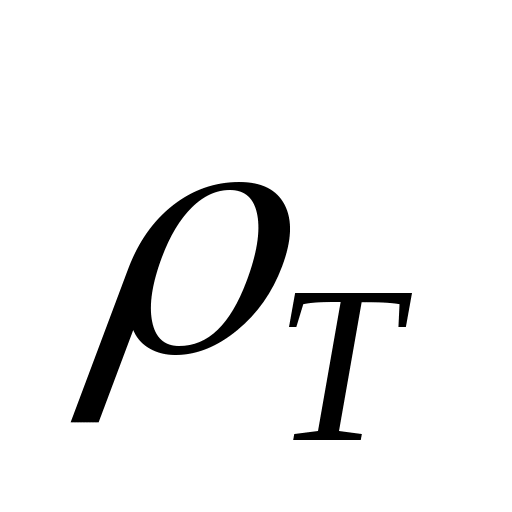 – сопротивление, обусловленное рассеянием электронов на тепловых колебаниях решетки; – сопротивление, обусловленное рассеянием электронов на тепловых колебаниях решетки; 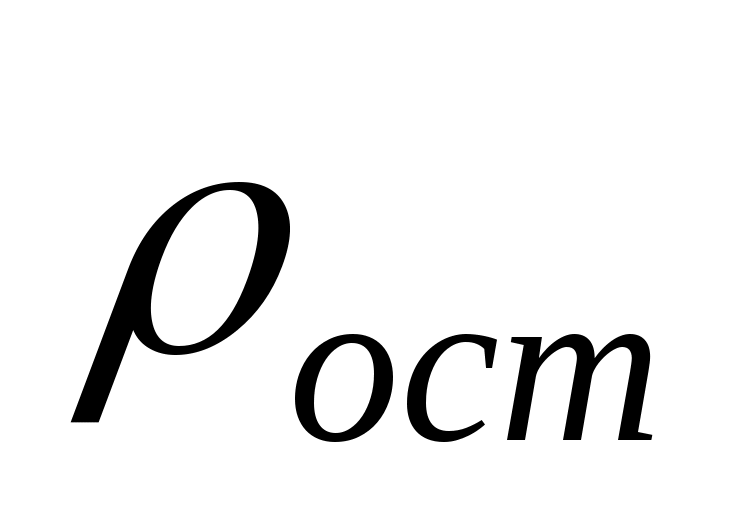 – остаточное сопротивление, связанное с рассеянием электронов на неоднородностях структуры. Для чистой меди – остаточное сопротивление, связанное с рассеянием электронов на неоднородностях структуры. Для чистой меди 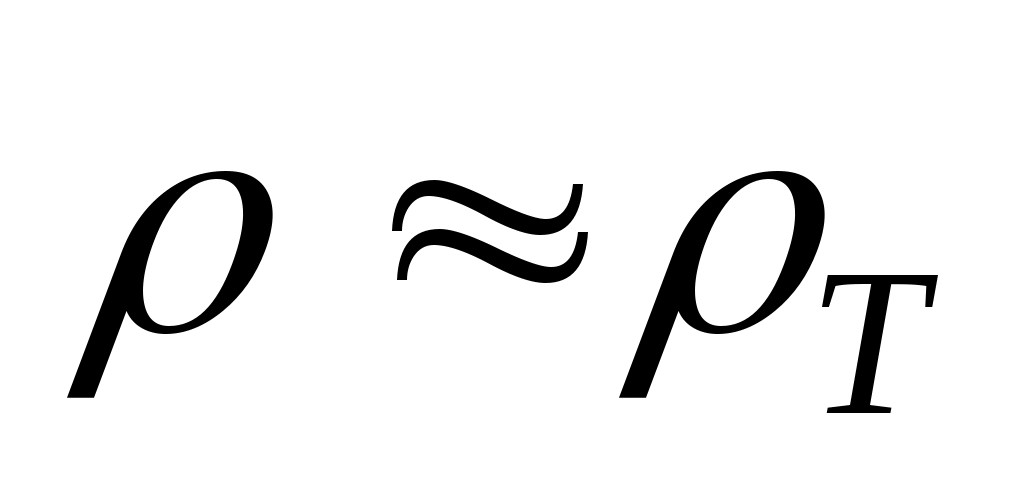 . При Т=300 К . При Т=300 К 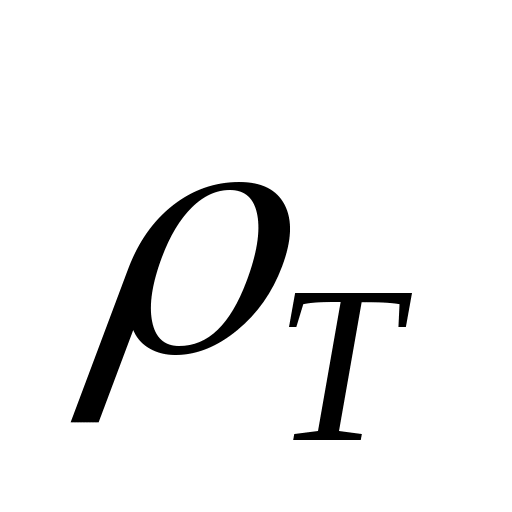 = 0,0168 мкОмм (см. Приложение). Вблизи температуры абсолютного нуля полное сопротивление реального металлического проводника равно остаточному сопротивлению. Отсюда следует, что = 0,0168 мкОмм (см. Приложение). Вблизи температуры абсолютного нуля полное сопротивление реального металлического проводника равно остаточному сопротивлению. Отсюда следует, что
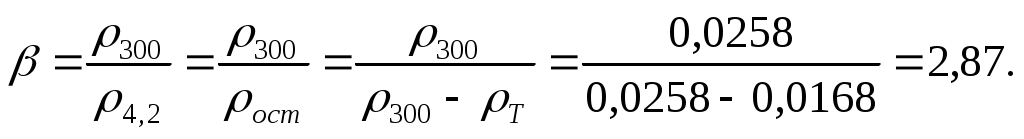
5 Сопротивление вольфрамовой нити электрической лампочки при 20 оС равно 35 Ом. Определить температуру нити лампочки, если известно, что при включении в сеть напряжением 220 В в установившемся режиме по нити проходит ток 0,6 А. Температурный коэффициент удельного сопротивления вольфрама при 20 оС равен 510–3 К–1.
Решение
С учетом линейной зависимости сопротивления металлического проводника от температуры имеем: 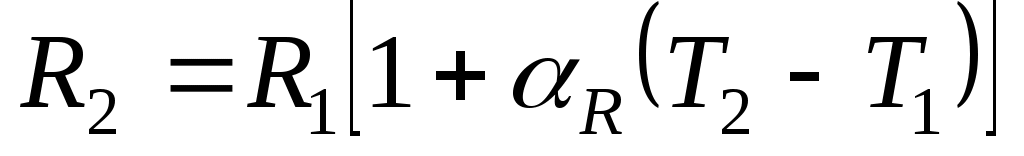 , где , где 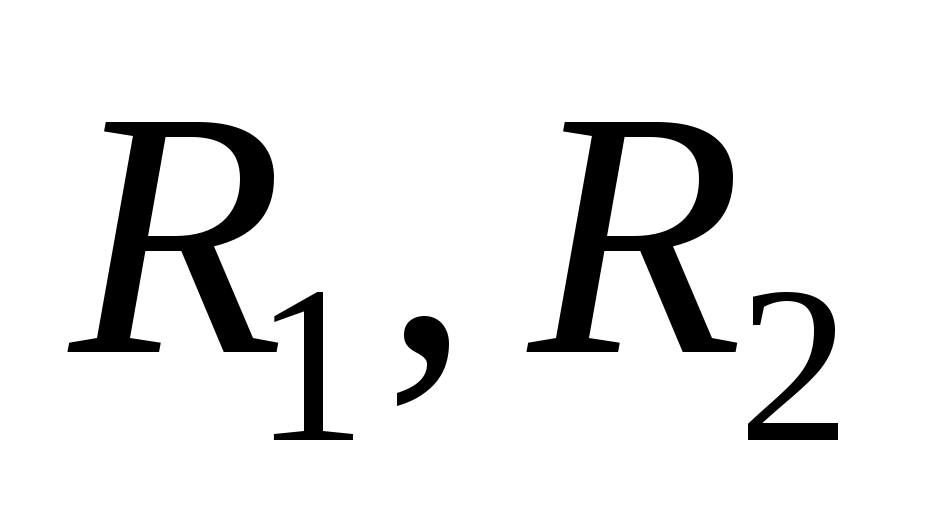 – сопротивления при комнатной температуре – сопротивления при комнатной температуре 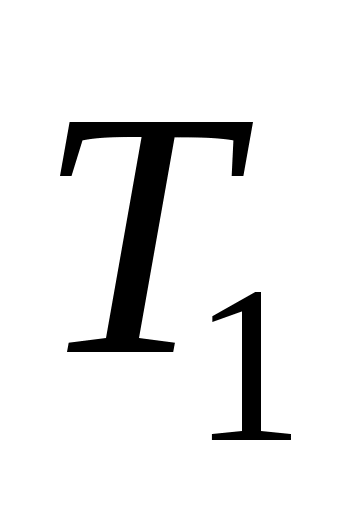 и при температуре и при температуре 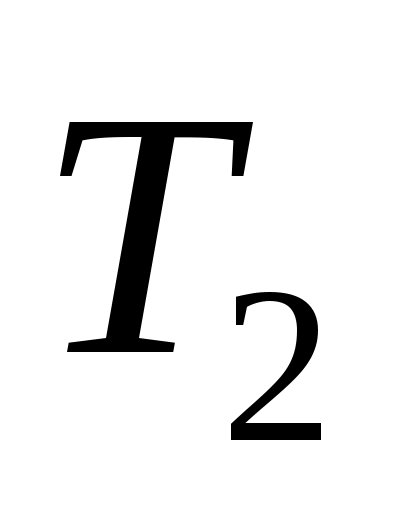 соответственно. Для вольфрама можно считать, что соответственно. Для вольфрама можно считать, что 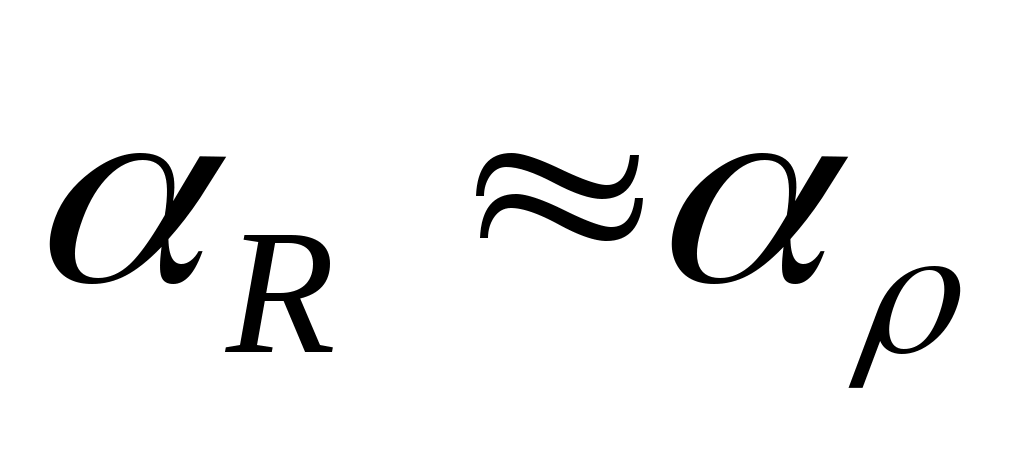 . Сопротивление нити лампочки в рабочем режиме . Сопротивление нити лампочки в рабочем режиме
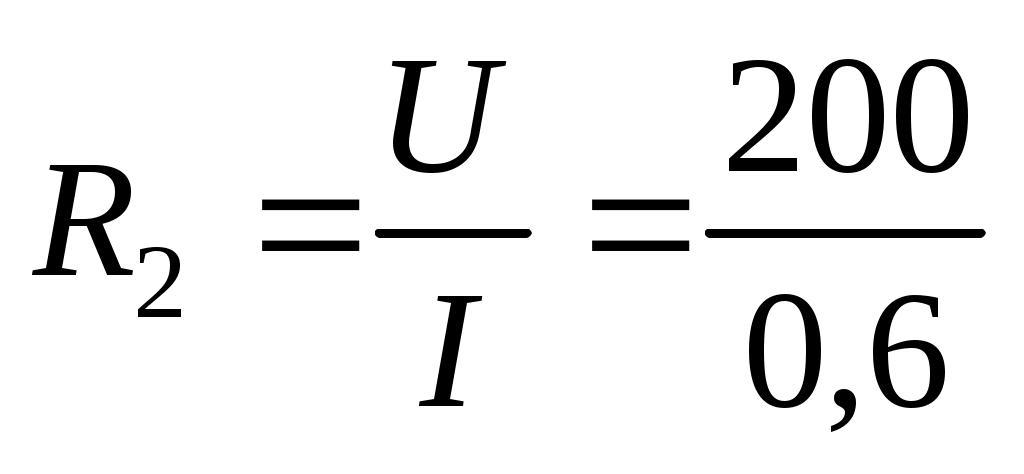 =366, Ом. =366, Ом.
Тогда
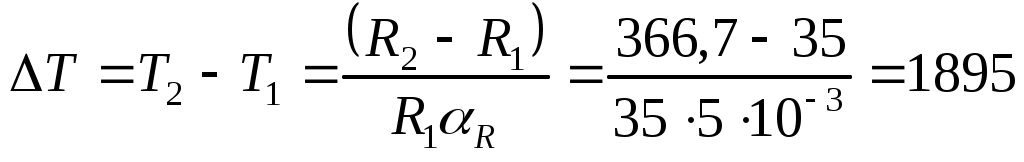 К. К.
Окончательно имеем 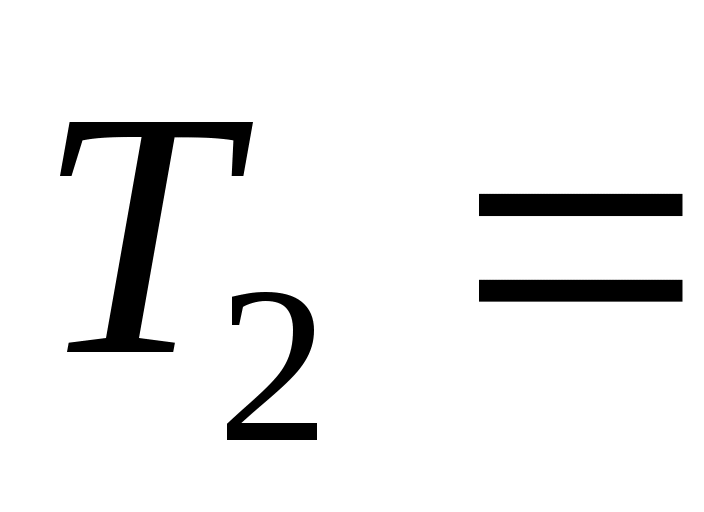 1895+293 =2188 К. 1895+293 =2188 К.
Пояснение: В общем виде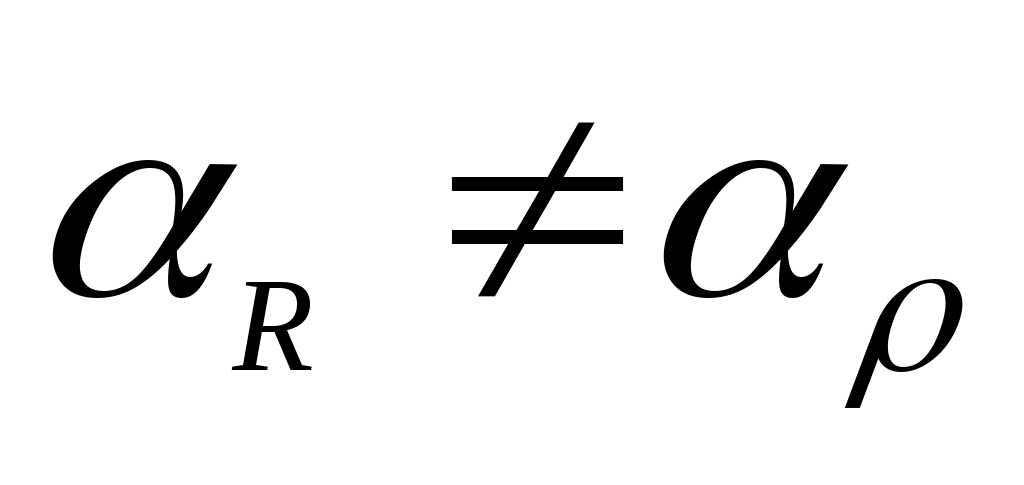 , т.к. l и S также зависят от Т. , т.к. l и S также зависят от Т.
6 Вычислить, во сколько раз сопротивление 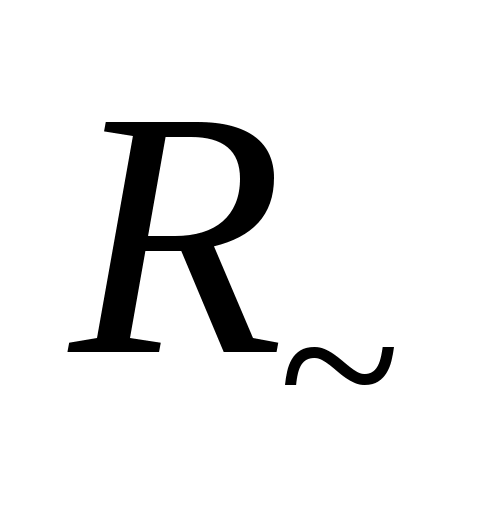 медного провода круглого сечения диаметром медного провода круглого сечения диаметром 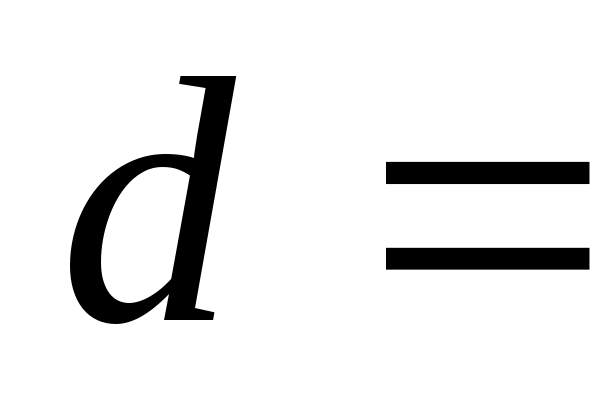 1 мм на частоте 1 мм на частоте 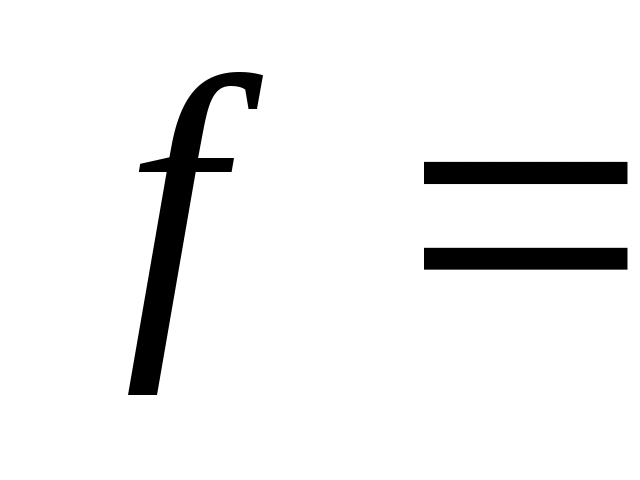 10 МГц больше сопротивления 10 МГц больше сопротивления 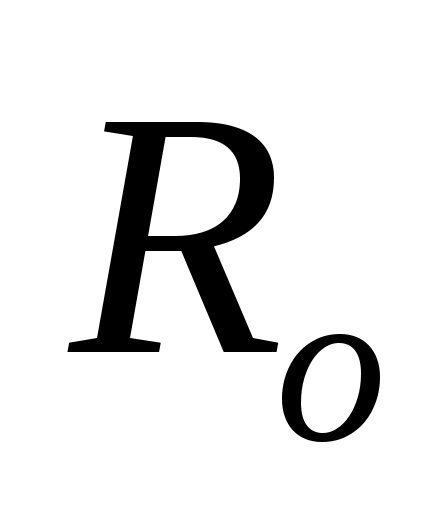 этого провода постоянному электрическому току. этого провода постоянному электрическому току.
Решение
Глубина проникновения электромагнитного поля в проводник 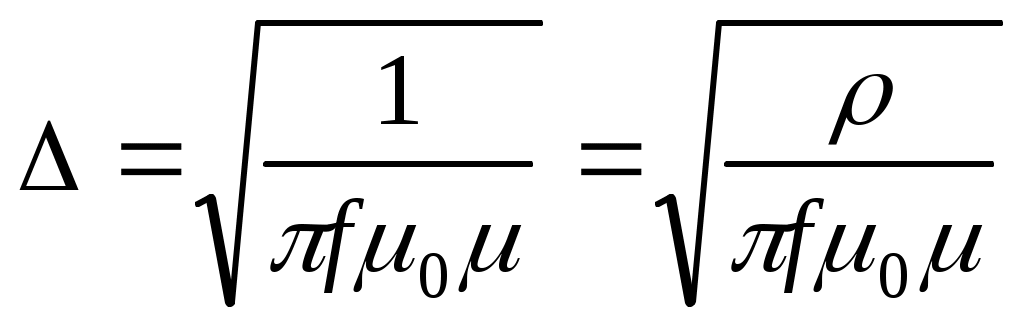 , где , где 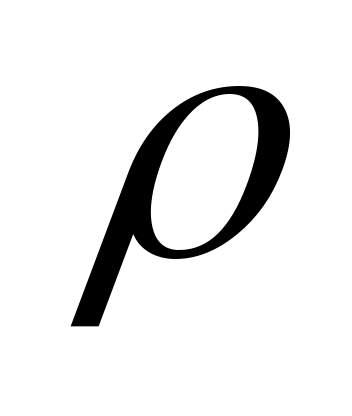 – удельное сопротивление проводника; – удельное сопротивление проводника; 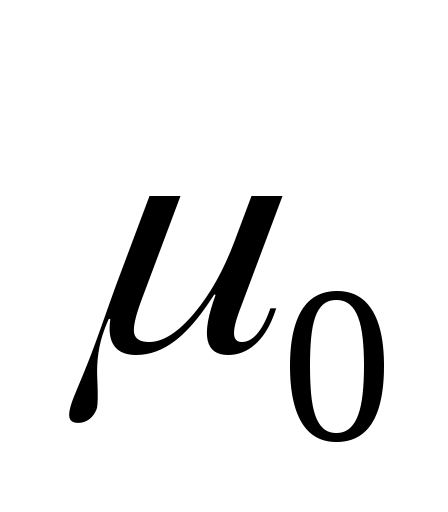 – магнитная постоянная; – магнитная постоянная; 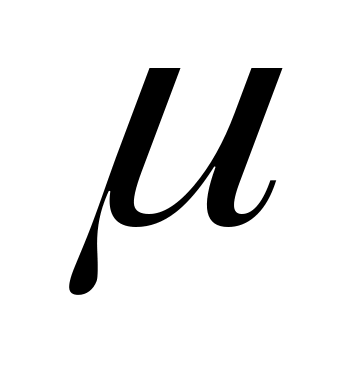 – относительная магнитная проницаемость материала. Поскольку медь диамагнитна, – относительная магнитная проницаемость материала. Поскольку медь диамагнитна, 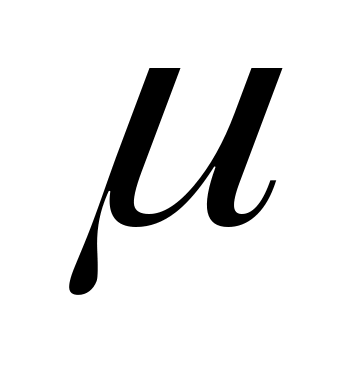 =1. Тогда для меди на частоте 10 МГц =1. Тогда для меди на частоте 10 МГц
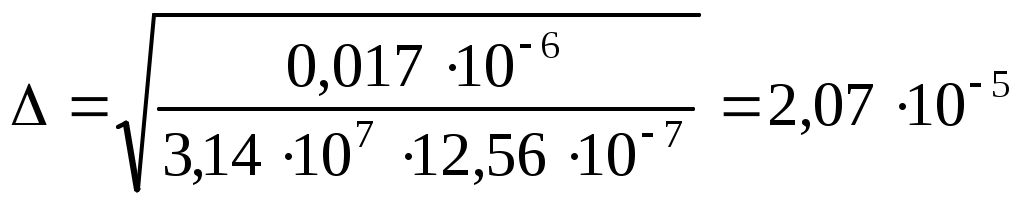 м. м.
Как видно, , т.е. сильно выраженный поверхностный эффект, а в этом случае коэффициент увеличения сопротивления провода круглого сечения обратно пропорционален отношению площадей, по которым протекает ток. , т.е. сильно выраженный поверхностный эффект, а в этом случае коэффициент увеличения сопротивления провода круглого сечения обратно пропорционален отношению площадей, по которым протекает ток.
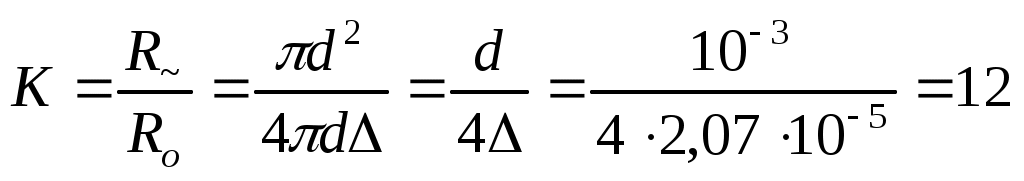 . .
7 Определить сопротивление шайбового высокочастотного резистора, изготовленного из пленки углерода с удельным поверхностным сопротивлением 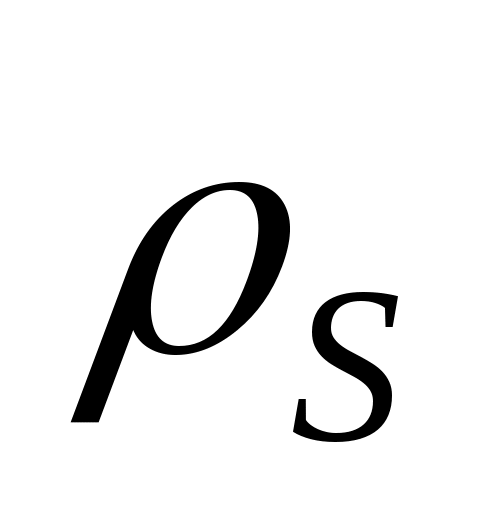 =300 Ом (см. рисунок). Размеры резистивного эле-мента: =300 Ом (см. рисунок). Размеры резистивного эле-мента: 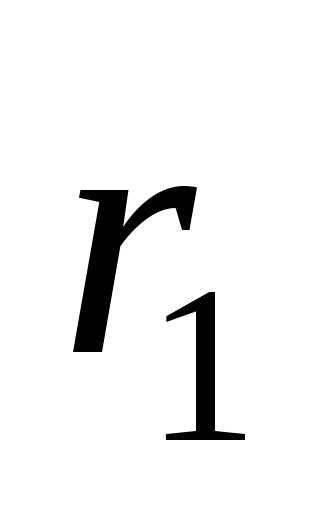 = 3 мм, = 3 мм, 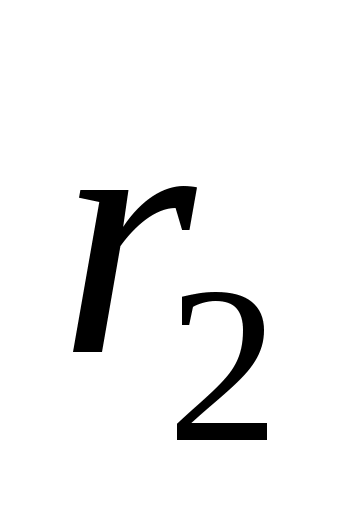 = 7 мм. = 7 мм.
Р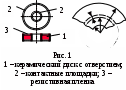 ешение ешение
Ток через такой резистор проходит радиально по резистивной пленке. Выделим в пределах резистивного элемента узкий кольцеобразный участок шириной 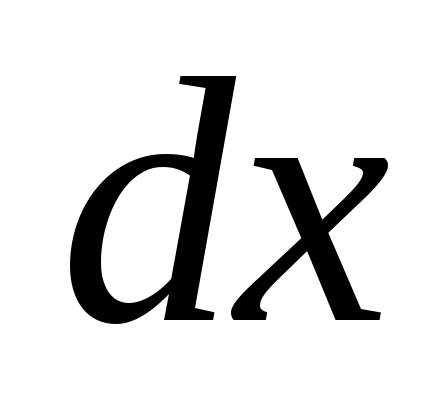 , имеющий координату , имеющий координату 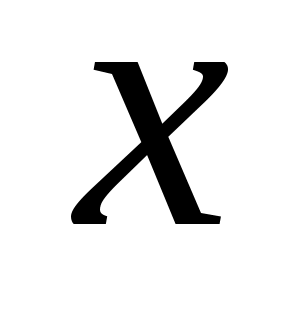 , отсчитываемую от центра. Сопротивление этого участка , отсчитываемую от центра. Сопротивление этого участка 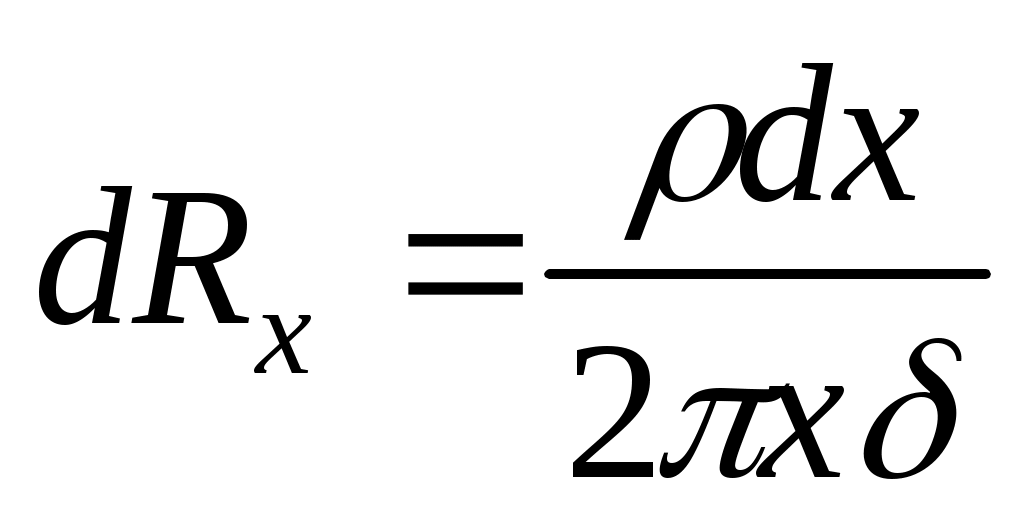 , где , где 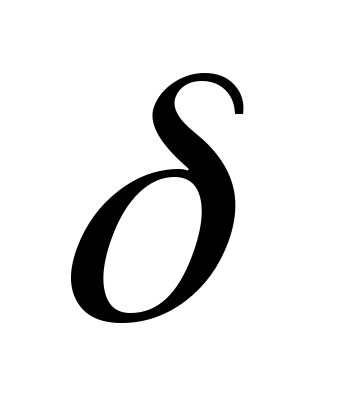 –толщина пленки, –толщина пленки, 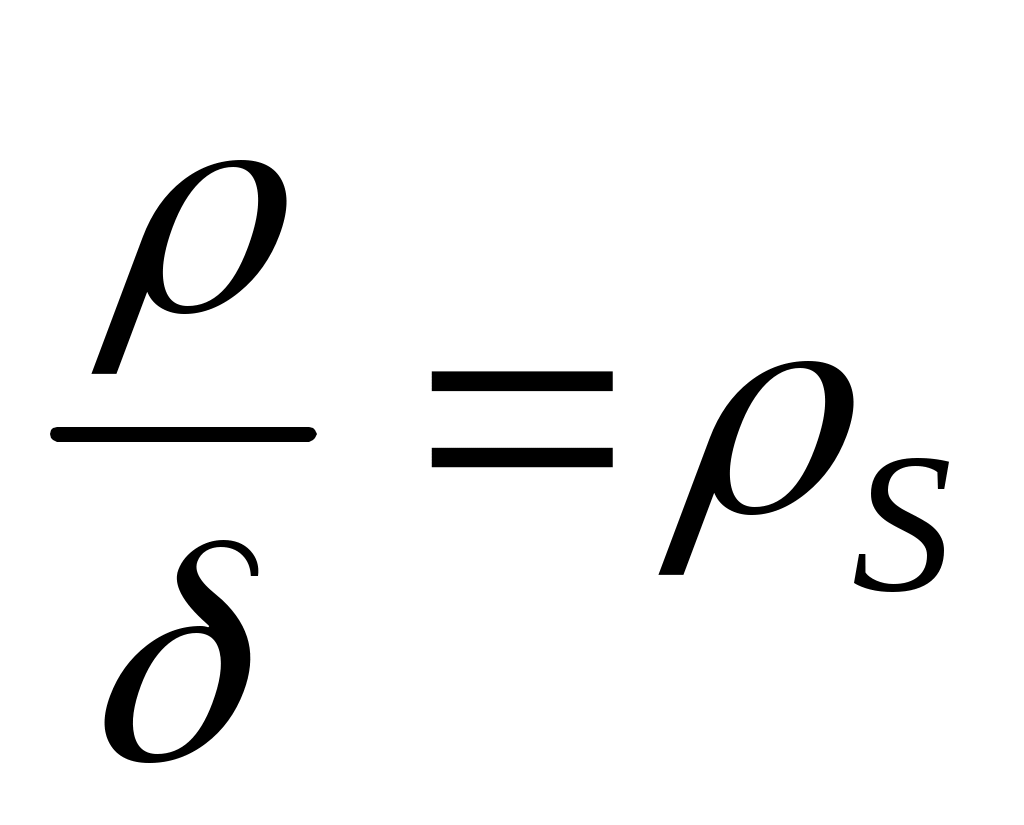 – сопротивление квадрата резистивной пленки. – сопротивление квадрата резистивной пленки.
Сопротивление резистивного элемента, расположенного с одной стороны диэлектрического диска с отверстием (шайбы): 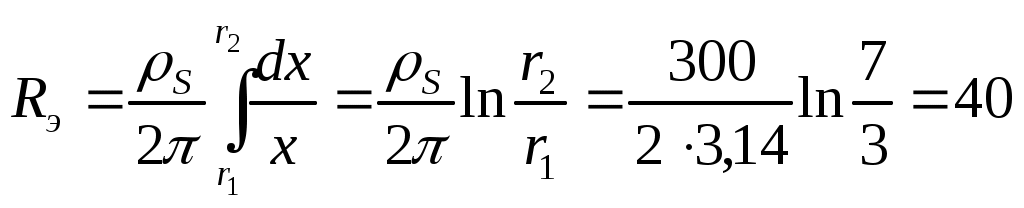 Ом. Ом.
Резистор содержит два таких элемента, включенных параллельно, т.е. сопротивление резистора 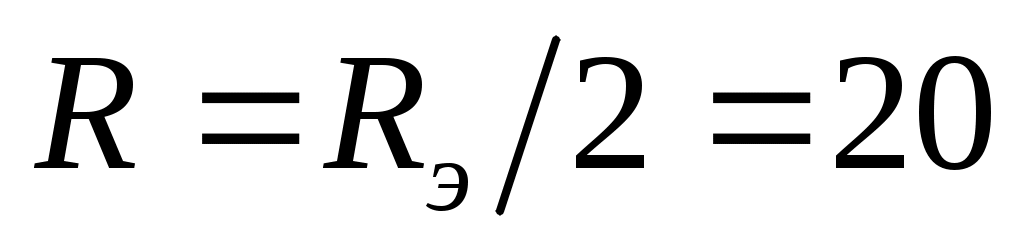 Ом. Ом.
8 Определить время, в течение которого электрон пройдет расстояние 1 км по медному проводу, если удельное сопротивление меди 0,017 мкОмм, а разность потенциалов на концах проводника = 220 В.
Решение
Из закона Ома следует, что удельная проводимость 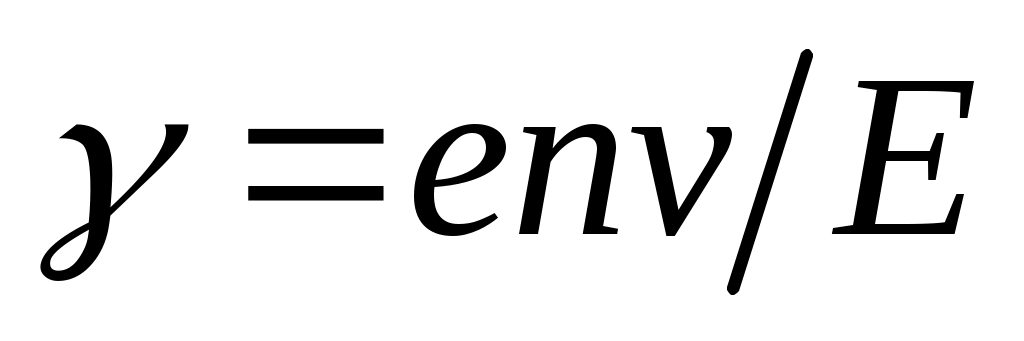 . Концентрация свободных электронов в меди: . Концентрация свободных электронов в меди: 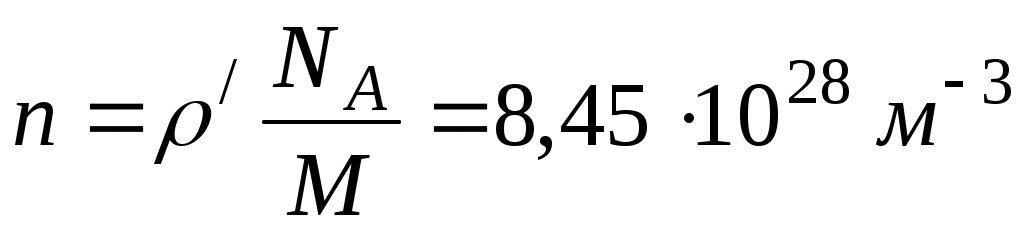 , где , где 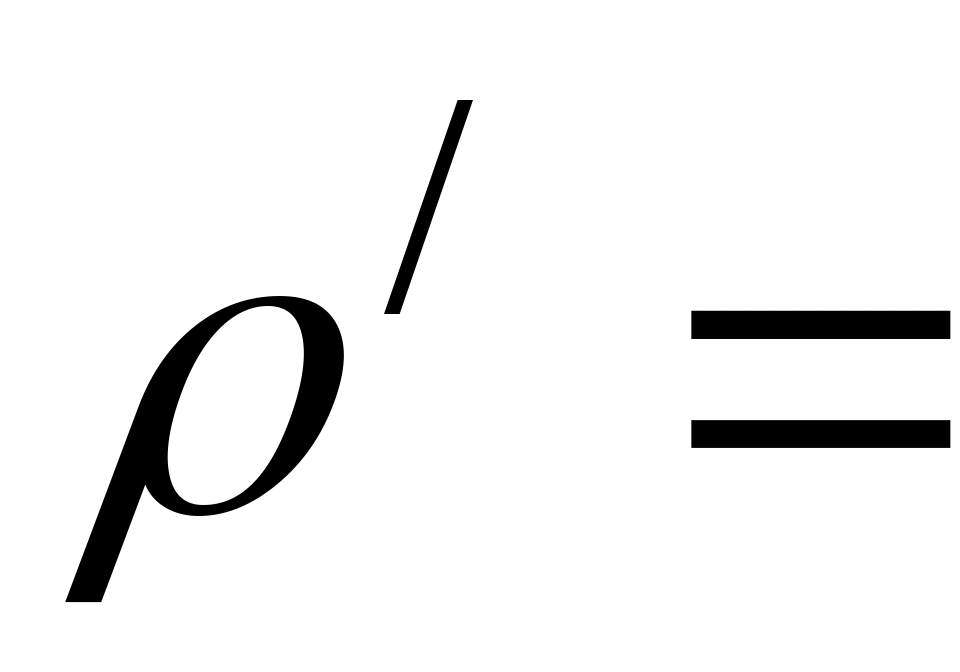 8920 кг/м3 – плотность меди, 8920 кг/м3 – плотность меди, 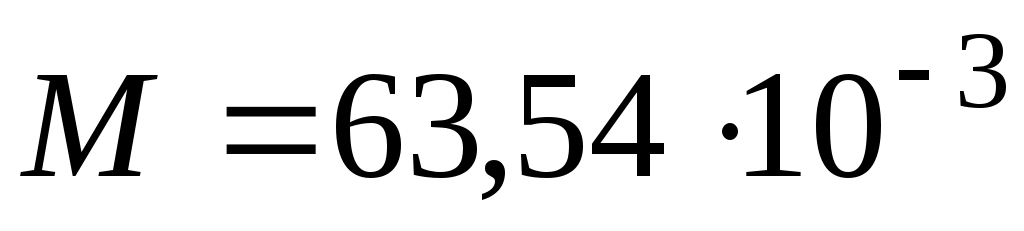 кг/моль, кг/моль, 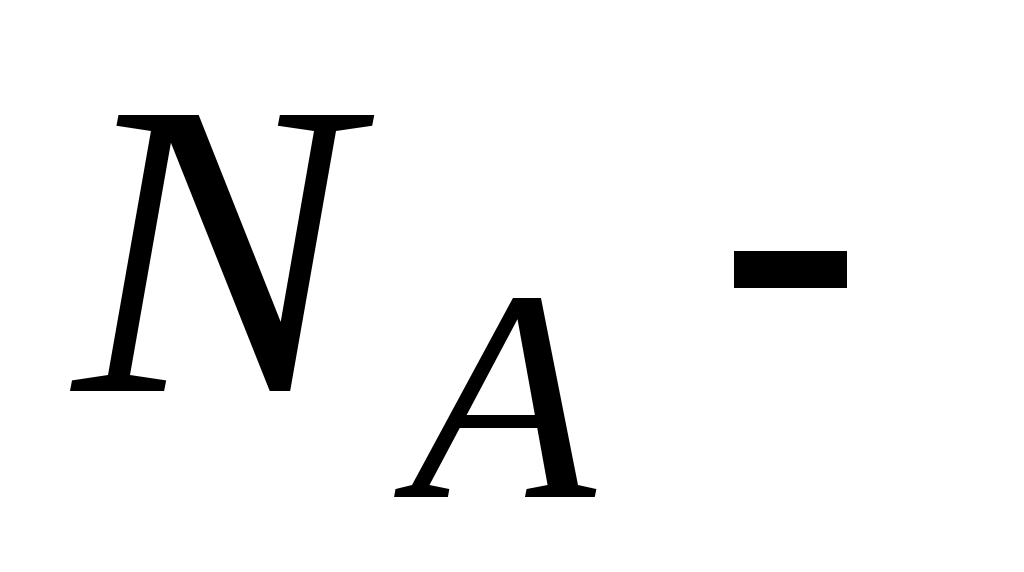 число Авогадро. Тогда средняя скорость дрейфа электронов число Авогадро. Тогда средняя скорость дрейфа электронов 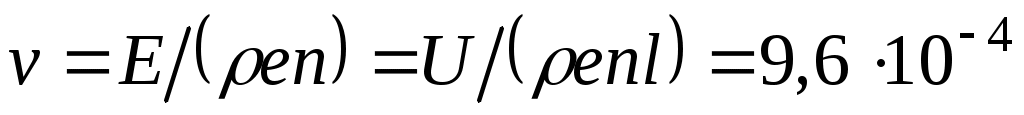 м/с. м/с.
|
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.
 ешение
ешение 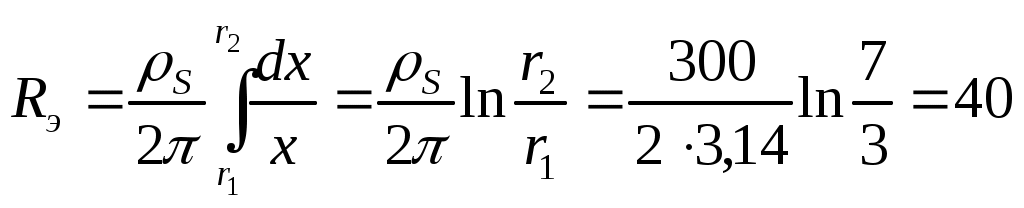 Ом.
Ом.