Методические рекомендации и указания

• Название: Методические рекомендации и указания
• Дата: 16.03.2023
• Размер: 0.62 Mb.
• Имя файла: 82487.doc
• Тип: Методические рекомендации; #994608
• страница: 5 из 6

1.4 Полупроводники

18 Найти положение уровня Ферми в собственном германии при 300 К, если известно, что ширина запрещенной зоны = 0,665 эВ, а эффективные массы плотности состояний для дырок валентной зоны и для электронов зоны проводимости соответственно равны: =0,388 ; = 0,55 , где – масса свободного электрона.

Решение

Положение уровня Ферми в собственном полупроводнике определяется выражением:

,

где 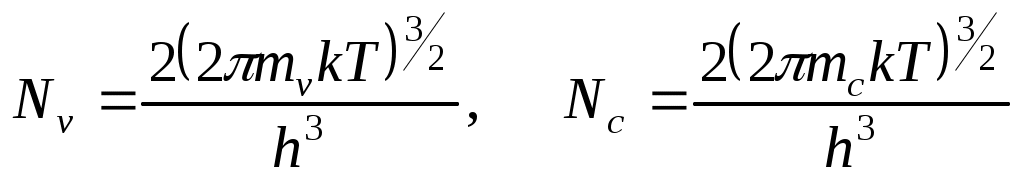– уровень, соответствующий середине запрещенной зоны;

– эффективная плотность состояний для дырок валентной зоны и для электронов зоны проводимости соответственно.

. Подставляя значения физических констант , а также температуру, получим: м^–3, м^–3. Таким образом,

Дж =

= –6,7810^–3 эВ.

Из-за малых значений энергия в физике полупроводников, как правило, вычисляется в электрон-вольтах (эВ). 1 эВ = 1,610^–19 Дж.

Таким образом, уровень Ферми в собственном германии при комнатной температуре расположен на 6,78 мэВ ниже середины запрещенной зоны.
19 Вычислить собственную концентрацию носителей заряда в кремнии при = 300 К, если ширина запрещенной зоны = 1,12 эВ, а эффективные массы плотности состояний .

Решение

Собственная концентрация носителей заряда

.

Эффективная плотность состояний для электронов в зоне проводимости и для дырок в валентной зоне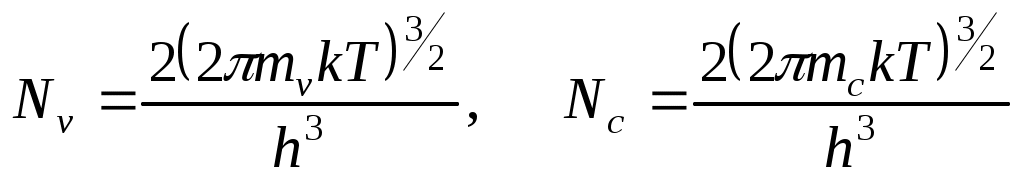

.

Отсюда следует, что собственная концентрация: м^–3.
20 Вычислить положение уровня Ферми при = 300 К в германии, содержащем 210²² м^–3 атомов мышьяка и 10²² м^–3 атомов галлия. Эффективная масса плотности состояний в зоне проводимости = 0,55 .

Решение

Галлий (элемент 3 группы) является донором для германия, а мышьяк (5 группа) – акцептором. Так как 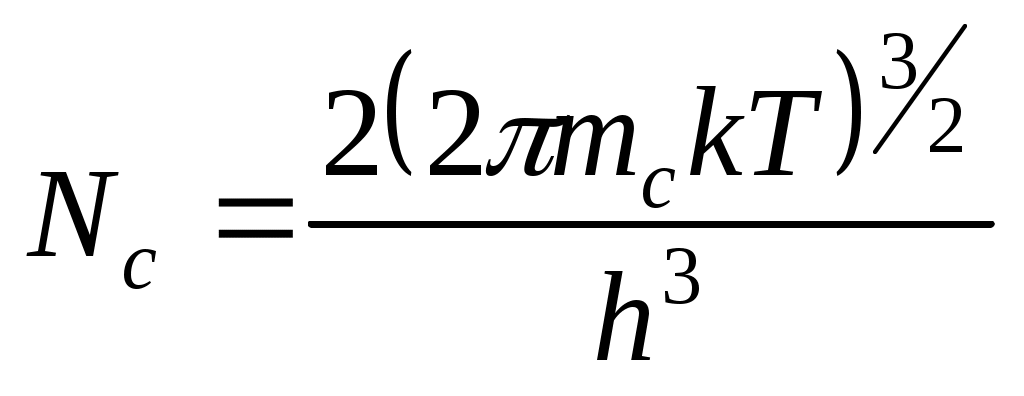, то такой частично компенсированный полупроводник обладает электропроводностью -типа. При этом избыточная концентрация доноров . При комнатной температуре все примеси ионизированы, поэтому концентрация электронов в зоне проводимости приблизительно равна избыточной концентрации доноров: . Из выражения, связывающего концентрацию электронов в зоне проводимости с положением уровня Ферми относительно дна зоны проводимости, найдем искомое положение уровня Ферми относительно дна зоны проводимости:

, где = 1,0210²⁵ м^–3,

, Дж =

= 0,179 эВ.

Из-за малых значений энергия в физике полупроводников, как правило, вычисляется в электрон-вольтах (эВ). 1 эВ = 1,610^–19 Дж
21 Рассчитать концентрацию электронов и дырок в германии -типа с удельным сопротивлением 0,05 Омм при температуре 300 К. Собственная концентрация носителей заряда при комнатной температуре = 2,110¹⁹ м^–3, подвижность электронов = 0,39 м²/(Вс), подвижность дырок = 0,19 м²/(Вс).

Решение

Удельное сопротивление связано с концентрацией электронов и дырок уравнением

, .

Для концентрации дырок получаем квадратное уравнение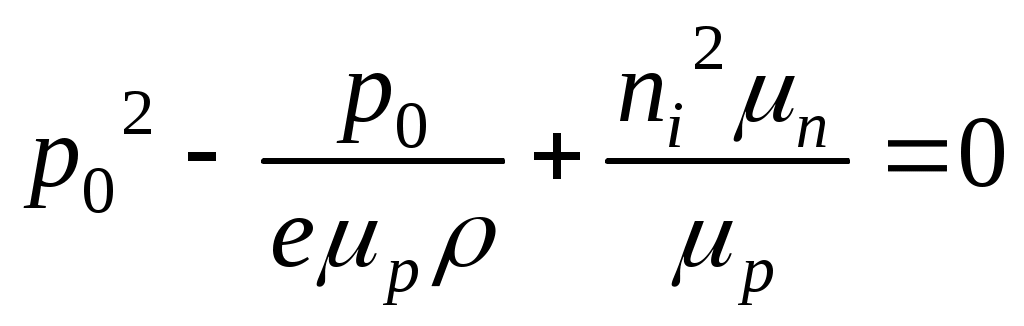

.

Подставляя исходные данные, имеем:

,

откуда 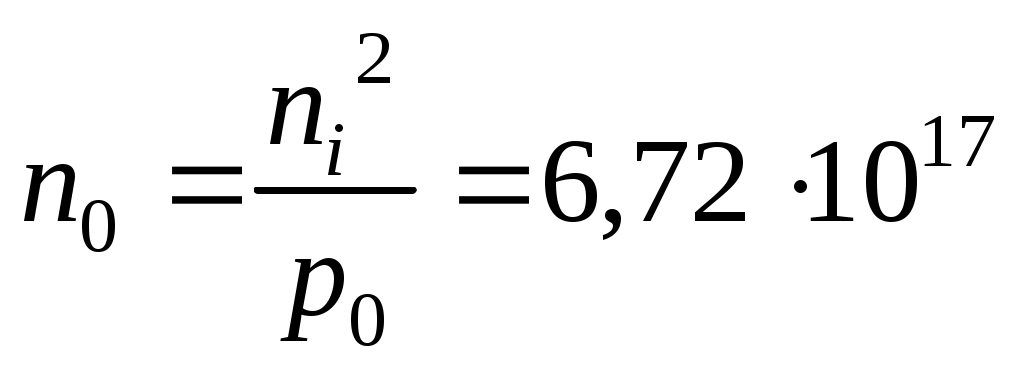м^–3. Второе решение квадратного уравнения отбрасываем, так как оно соответствует полупроводнику -типа.

м^–3.
22 В идеально скомпенсированном полупроводнике концентрация электронов равна концентрации дырок. Можно ли считать, что при всех температурах удельное сопротивление такого полупроводника равно собственному удельному сопротивлению?

Решение

В скомпенсированном полупроводнике больше, чем в собственном нарушений периодического потенциала кристаллической решетки, вызывающих рассеяние носителей заряда. Такими нарушениями являются ионизированные доноры и акцепторы. Различия в подвижности носителей заряда, а значит, и в удельном сопротивлении собственного и скомпенсированного полупроводников сильнее проявляются в области более низких температур.
23 Определить скорость оптической генерации неравновесных носителей заряда в пластине кремния на глубине 100 мкм от освещаемой поверхности при фотовозбуждении монохроматическим излучением интенсивностью 10²⁰ м^–2с^–2, если показатель поглощения материала 510⁴ м^–1, а коэффициент отражения излучения от поверхности равен 0,3.

Решение

Скорость оптической генерации, т.е. число носителей заряда, возбуждаемых светом в единицу времени в единице объема полупроводника, зависит от показателя поглощения и интенсивности излучения на заданной глубине . Изменение интенсивности излучения подчиняется закону Бугера-Ламберта

,

где – интенсивность на глубине ;

– коэффициент отражения излучения;

– показатель поглощения материала.

Число квантов, поглощаемых в слое единичной площади толщиной , определяется выражением . Скорость оптической генерации

2,3610²² м^–3с^–1.