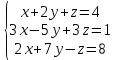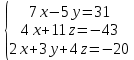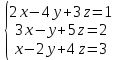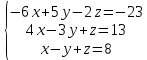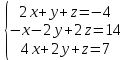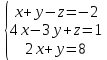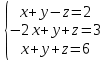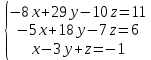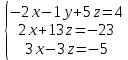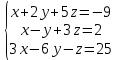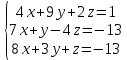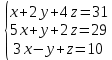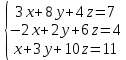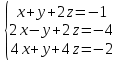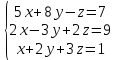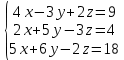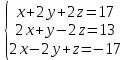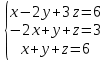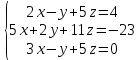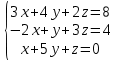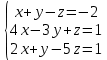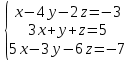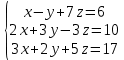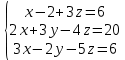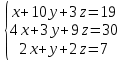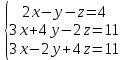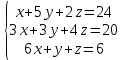Решить систему уравнений матричным методом (с помощью обратной матрицы), по правилу Крамера или методом Гаусса.
Даны координаты вершин треугольника ABC.
Найти: 1) уравнения сторон треугольника;
2) уравнение высоты СН, опущенной из вершины C на сторону AB;
3) уравнение медианы к стороне AC;
4) угол A;
5) сделать чертеж в системе декартовой координат OХУ
|
A(1, 5), B(5, 2), C(1, 2).
|
|
A(1, 2), B(5, 5), C(5, 2).
|
|
A(5, 2), B(1, 5), C(5, 5
|
|
A(5, 5), B(1, 2), C(1, 5).
|
|
A(−4, 0), B(−1, 6), C(−5, 6)
|
|
A(−2, 3), B(−6, 6), C(−2, 6)
|
|
A(−2, 6), B(−6, 3), C(−6, 6)
|
|
A(−6, 6), B(−2, 3), C(−6, 3)
|
|
A(−5, −1), B(−2, −5), C(−2, −1)
|
|
A(−2, −1), B(−5, −5), C(−2, −5)
|
|
A(−2, −5), B(−5, −1), C(−5, −5)
|
|
A(−5, −5), B(−2, −1), C(−5, −1)
|
|
A(3, −1), B(8, −4), C(8, −1)
|
|
A(8, −1), B(3, −4), C(8, −4)
|
|
A(8, −4), B(3, −1), C(3, −4)
|
|
A(3, −4), B(8, −1), C(3, −1)
|
|
A(−2, 3), B(4, 3), C(2, 5)
|
|
A(0, 1), B(4, 3), C(2, 5)
|
|
A(−2, 3), B(4, 3), C(0, 1)
|
|
A(−2, 3), B(2, 5), C(0, 1)
|
|
A(0, 1), B(4, 3), C(2, −1)
|
|
A(2, −1), B(2, 5), C(4, 3)
|
|
A(−5, 2), B(−5, 4), C(−3, 0)
|
|
A(−2, −2), B(4, −2), C(0, −4)
|
|
A(−2, −1), B(4, −2), C(2, 0)
|
|
A(2, 0), B(0, −4), C(4, −2)
|
|
A(−2, −2), B(0, −4), C(2, 0)
|
|
A(0, 2), B(2, 0), C(−2, −2)
|
Используя преобразование параллельного переноса, привести уравнение линии второго порядка к каноническому виду и схематично построить кривую.
|
a) 5x2 + 10x + 9y2 − 4 = 0
b) 4x − y2 − 2y − 5 = 0
|
|
a) 3x2 + 12x − y + 17 = 0
b) 4x2 + 16x − y2 − 6y + 11 = 0
|
|
a) x2 + 4x − 4y2 − 8y + 4 = 0
b) x2 + y2 − 2y + 3 = 0
|
|
a) 4x2 − 8x + 3y2 + 12y + 4 = 0
b) 2x2 − 16x + y + 35 = 0
|
|
a) 16x2 − 64x − 9y2 − 54y − 161 = 0
b) x2 + 10x − 2y + 11 = 0
|
|
a) x2 − 6x − 5y2 − 10y + 9 = 0
b) x2 + 4x + y + 9 = 0
|
|
a) 4x2 − 8x + 2y2 + 8y + 11 = 0
b) y2 − 8y + x + 21 = 0
|
|
a) x2 + 4x − 9y2 + 18y + 4 = 0
b) 3x2 − 6x − y + 1 = 0
|
|
a) x2 + 4x + 4y2 − 8y + 4 = 0
b) x + y2 − 4y + 9 = 0
|
|
a) x2 + 6x − 9y2 − 18y − 9 = 0
b) 4x2 − 8x − y + 1 = 0
|
|
a) 4x2 + 8x + 5y2 − 20y + 4 = 0
b) x + y2 − 2y + 2 = 0
|
|
a) 9x2 + 36x − 2y2 − 4y + 16 = 0
b) 2x2 − 4x − y = 0
|
|
a) 4x2 − 16x + 3y2 − 24y + 52 = 0
b) 5x − y2 − 2y − 11 = 0
|
|
a) 5x2 + 10x − y2 + 10y − 30 = 0
b) 3x2 + 30x − y + 77 = 0
|
|
a) 4x2 − 16x − 3y2 − 6y + 1 = 0
b) 2x2 − 4x + y + 7 = 0
|
|
a) 4x2 + 8x + y2 − 10y + 25 = 0
b) x − y2 + 2y + 3 = 0
|
|
a) 4x2 − 24x + 9y2 − 36y + 36 = 0
b) 3x − y2 − 2y − 4 = 0
|
|
a) 5x2 + 10x − y2 − 2y + 29 = 0
b) 4x2 + 8x − y − 1 = 0
|
|
a) 9x2 + 18x + 4y2 − 16y − 11 = 0
b) x + y2 + 2y + 3 = 0
|
|
a) x2 − y2 + 2y − 4 = 0
b) 2x2 + 20x − y + 48 = 0
|
|
a) 4x2 + 8x + 3y2 − 12y + 4 = 0
b) 4x2 + 8x + y + 6 = 0
|
|
a) x2 + 4x − 5y2 + 30y − 46 = 0
b) x − y2 − 2y − 5 = 0
|
|
a) 2x2 − 8x + y2 − 2y + 7 = 0
b) x + y2 − 2y + 3 = 0
|
|
a) 3x2 + 24x − y2 + 10y + 20 = 0
b) y2 + 2y − 4x − 11 = 0
|
|
a) x2 + 4x + 5y2 − 10y + 4 = 0
b) 4x2 − 8x − y + 1 = 0
|
|
a) 9x2 − 18x − 4y2 − 24y + 9 = 0
b) 3x − y2 − 2y − 16 = 0
|
|
a) x2 + 10x + 4y2 − 8y + 25 = 0
b) 2x2 + 4x + y + 3 = 0
|
|
a) x2 + 4x − 3y2 + 6y + 4 = 0
b) 4x − y2 + 2y + 11 = 0.
| |
 Скачать 6.51 Mb.
Скачать 6.51 Mb.