Методические рекомендации по выполнению итоговой контрольной работы для специальности 09. 02. 07
 Скачать 6.51 Mb. Скачать 6.51 Mb.
|
|
Задание 9. Вычислить значения выражений с использованием замечательных пределов 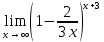 Решение: Проверим тип неопределенности, подставив х=∞ в функцию и получаем:  Данный предел можно свести к второму замечательному пределу. 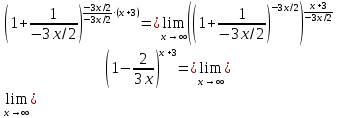 Выражение в скобках фактически и есть второй замечательный предел 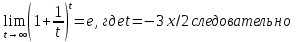 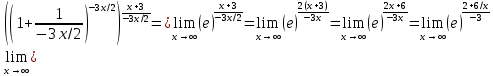  Ответ: е-2/3 З адание 10. Доказать, что функция  непрерывна в точке . непрерывна в точке .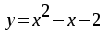 , х0=2 , х0=2Решение: Задание 11. Провести полное исследование функций и построить их графики. а) 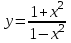 Р  ешение: ешение: б) 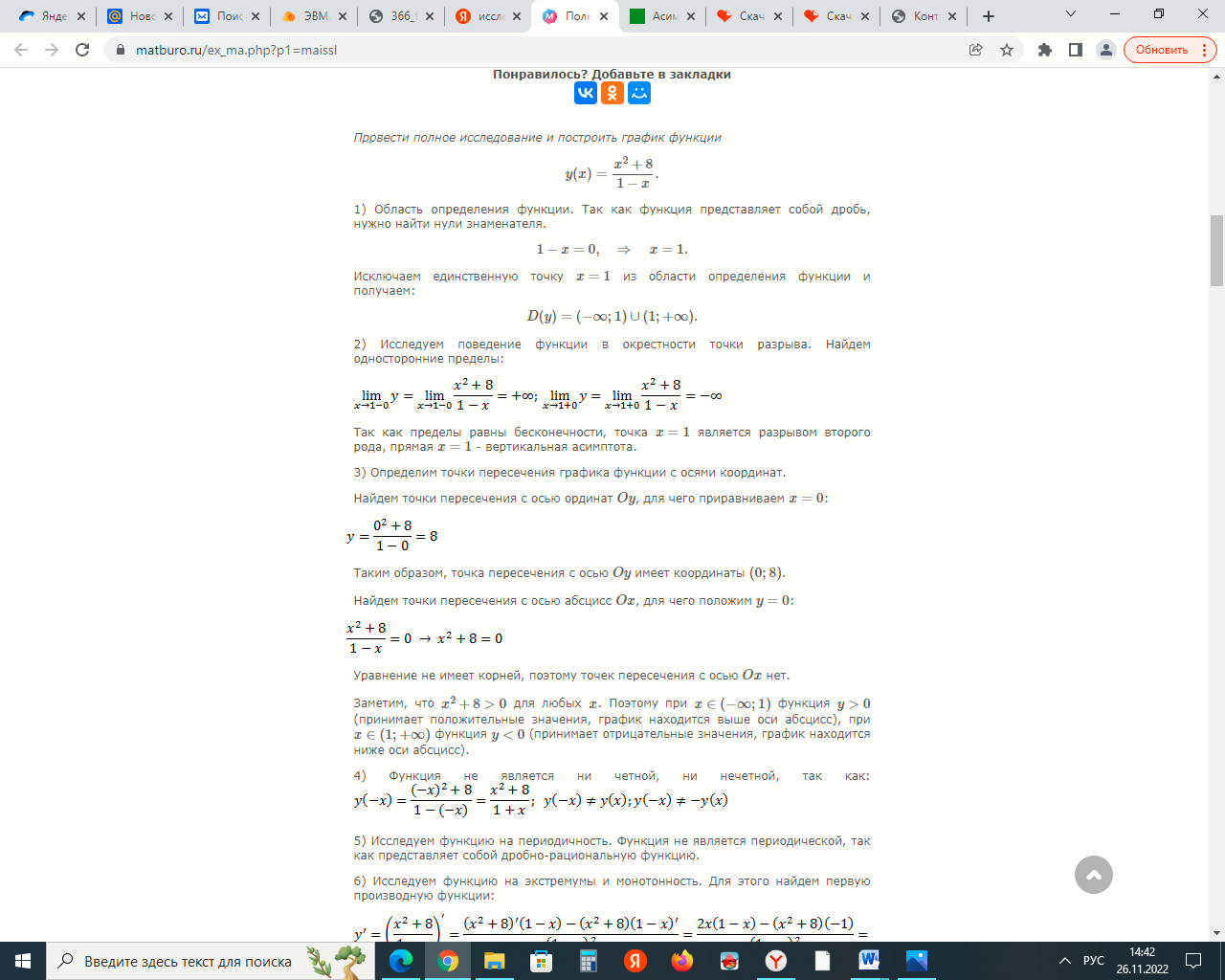   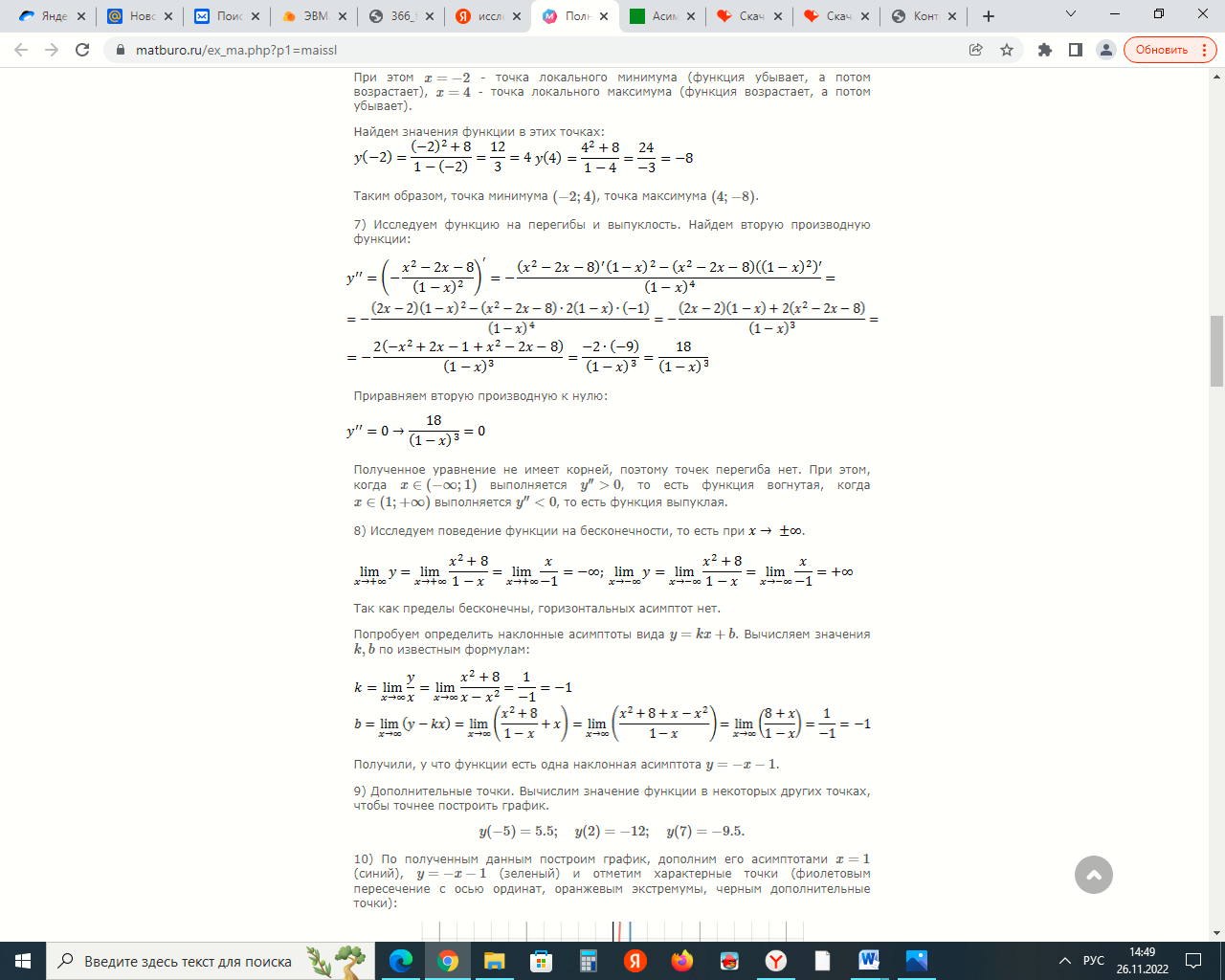 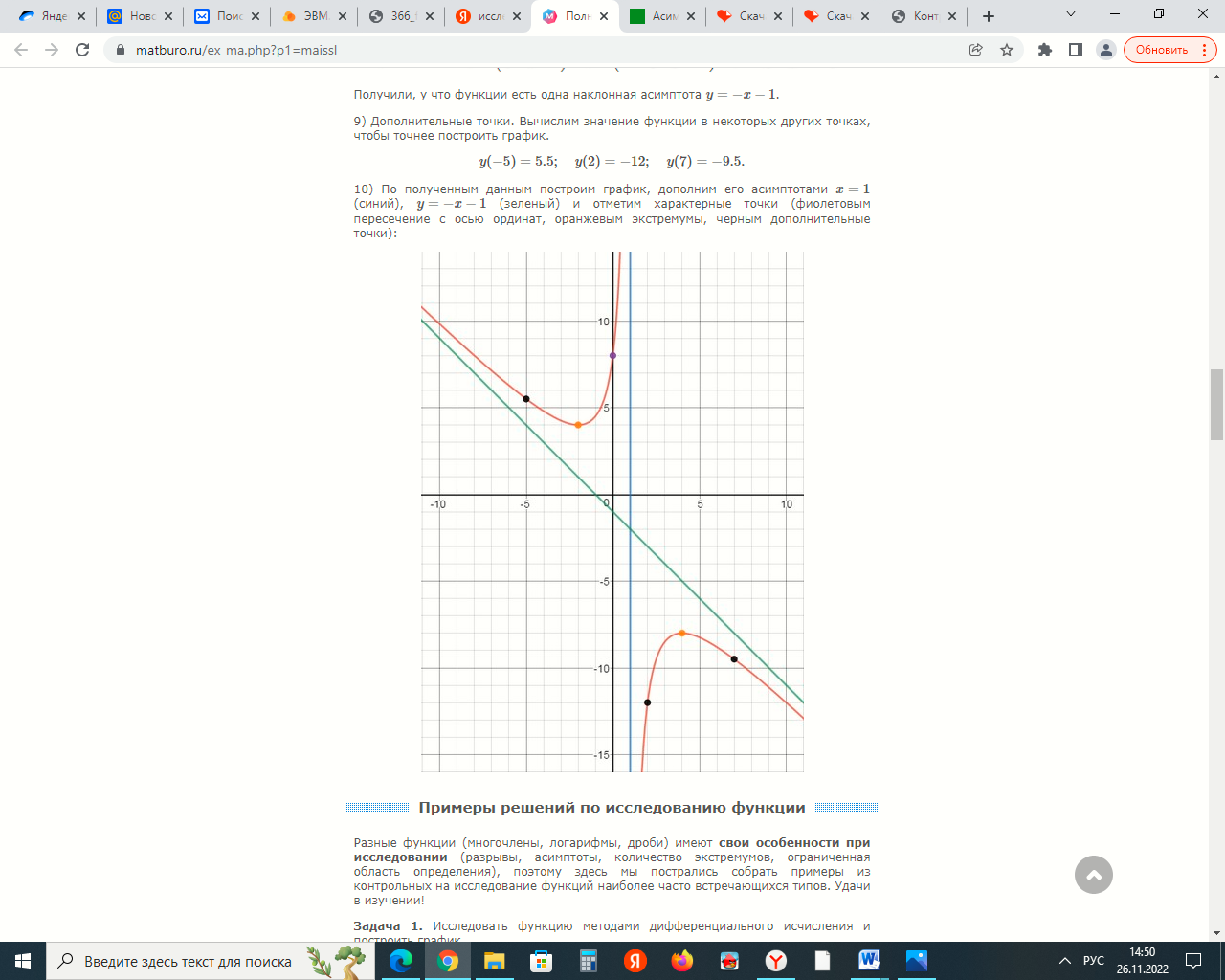 Задание 12. а) Вычислить производную функции 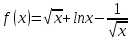 в точке x=4, в точке x=4, т.е найти 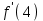 Решение: Для решения данного примера необходимо сначала найти производную, затем в полученное выражение поставить значение х. Для нахождения производной приведем корни к степенным функциям: 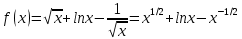 Применяя правило дифференцирования суммы и разности, а также формулы из таблицы производных, получаем: 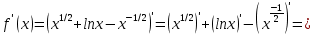 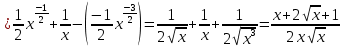 Подставим х = 4, получаем 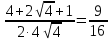 Ответ: 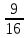 б) Найти производную функции 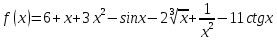 в точке х=0, т.е. найти в точке х=0, т.е. найти 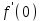 Решение: Для решения данного примера необходимо сначала найти производную, затем в полученное выражение поставить значение х. Для нахождения производной приведем корни к степенным функциям: 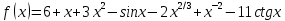 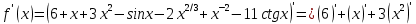 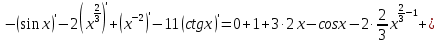 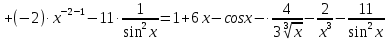 Ответ: 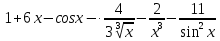 Задание 13. Вычислить вторую производную в точке х: 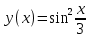 , x=1 , x=1 Решение: Найдем первую производную: 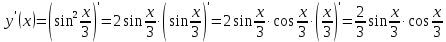 На каждом шаге смотрим, нельзя ли что-нибудь упростить. Воспользуемся формулой:  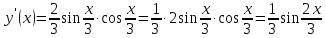 Находим вторую производную 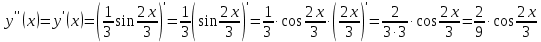 Подставляем в полученную производную 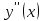 значение х=1. значение х=1.Получаем 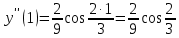 Ответ: 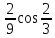 Задание 14. Вычислить неопределенный интеграл:  Задание 15. Вычислить неопределенный интеграл (методом интегрирования по частям) а) 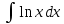 Решение: В искомом интеграле выделим функции u и v, затем выполним интегрирование по частям, используя формулу: 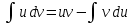 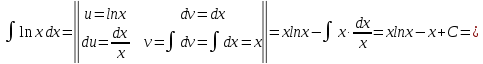  Ответ: 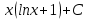 б  ) ) 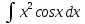 Решение: В искомом интеграле выделим функции u и v, затем выполним интегрирование по частям, используя формулу: 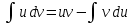 . Для решения данного интеграла эту операцию необходимо повторить 2 раза. . Для решения данного интеграла эту операцию необходимо повторить 2 раза.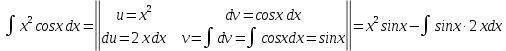 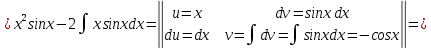 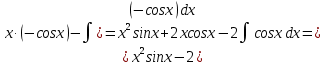 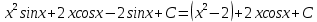 Ответ: 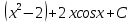 Задание 16. Вычислить определенный интеграл а) 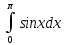 Решение: По таблице интегралов находим: 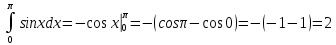 Ответ: 2 б)  Решение: По таблице интегралов находим: 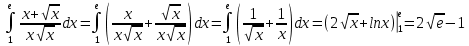 Ответ: 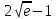 в) 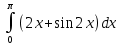 Решение: По таблице интегралов находим: 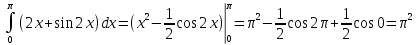 Ответ: 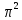 Задание 17. Вычислить площади фигур, ограниченных графиками функций 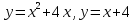   Задание 18. Найти общее решение дифференциального уравнения а) 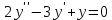 Решение: Имеем однородное линейное уравнение 2-го порядка с постоянными коэффициентами. Запишем и решим его характеристическое уравнение. Для этого, выполним замену  Получим 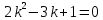 . . 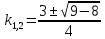 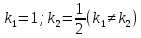 Поскольку корни характеристического уравнения действительные и различные, общее решение исходного дифференциального уравнения имеет вид 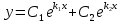 , где , где  – произвольные постоянные. – произвольные постоянные.Тогда, подставляя значения 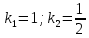 получаем общее решение уравнения получаем общее решение уравнения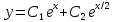 , , Ответ: 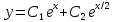 , , 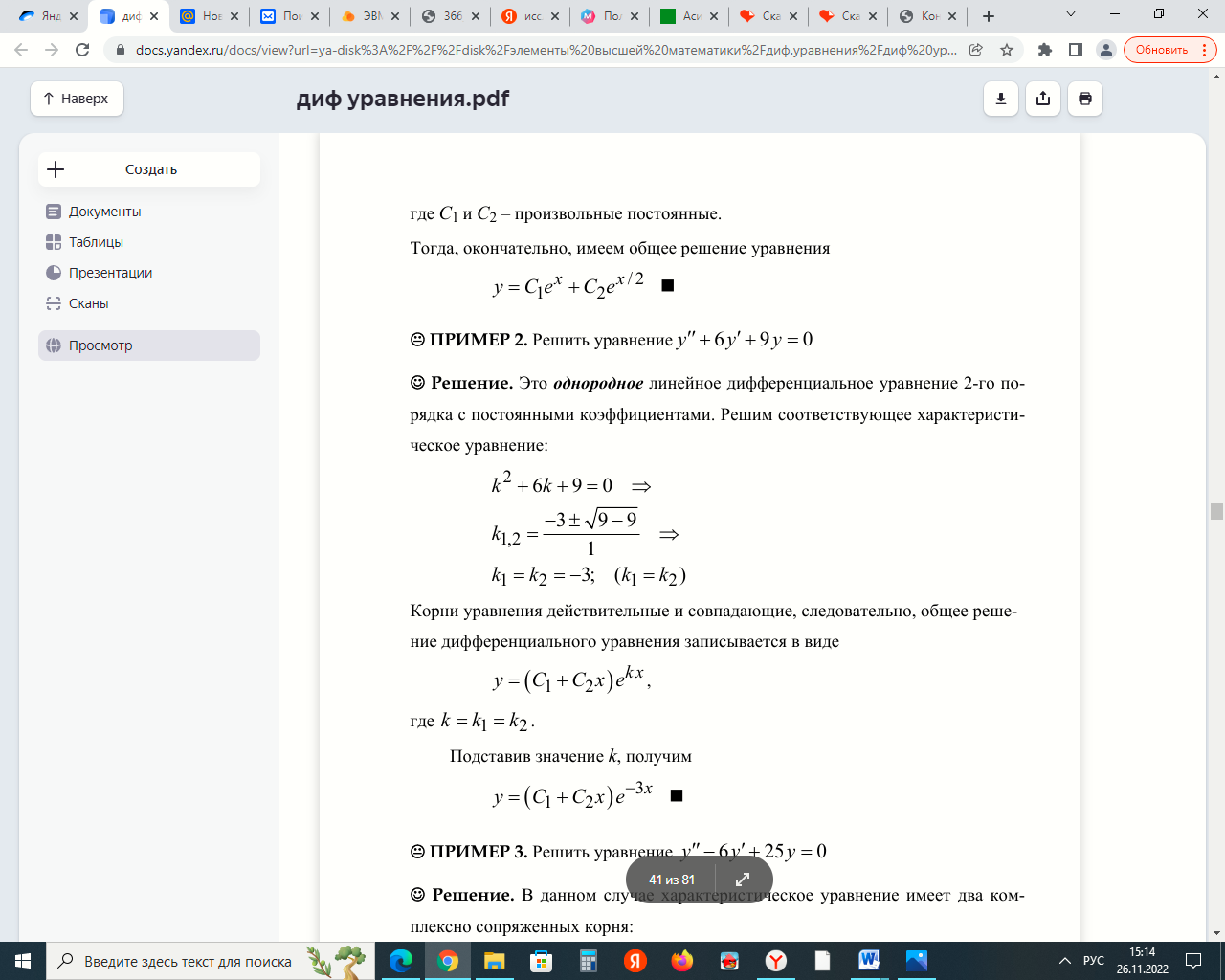  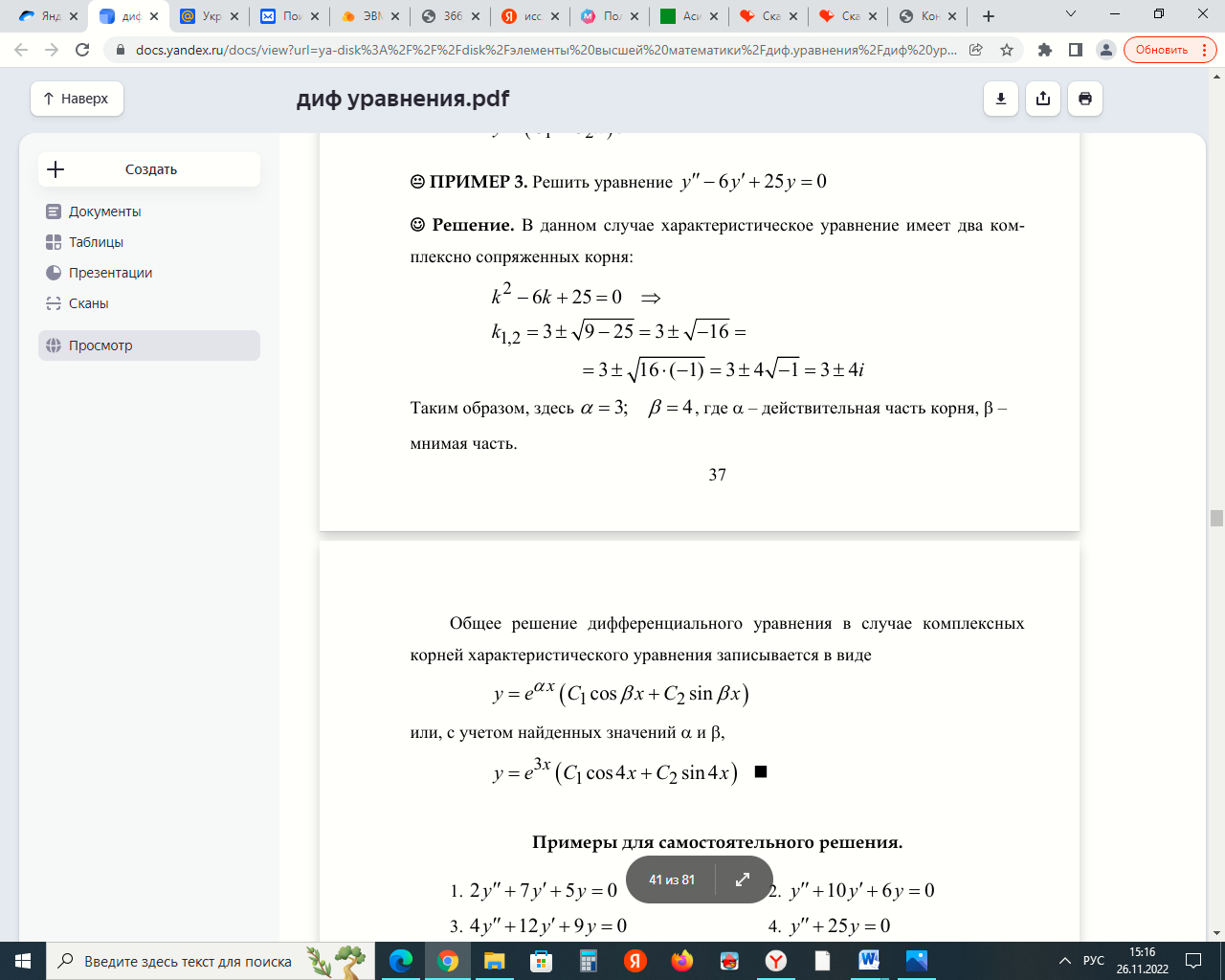  Задание 19. Найти общее решение дифференциального уравнения x(x-1) 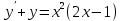 линейное неоднородное дифференциальное уравнение первого порядка. Будем искать его решение в виде линейное неоднородное дифференциальное уравнение первого порядка. Будем искать его решение в виде 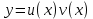 , тогда , тогда 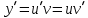 . Подставляем выражения для y и yʹ в исходное уравнение, . Подставляем выражения для y и yʹ в исходное уравнение,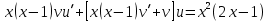 Функцию 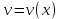 находим из условия находим из условия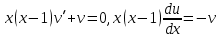 Разделяем переменные 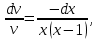 Интегрируем 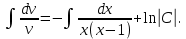 Вычислим интеграл 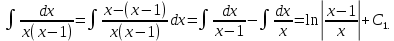 Окончательно получаем 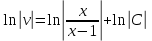 Откуда 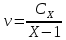 . Возьмём, например, частное решение . Возьмём, например, частное решение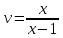 ,тогда получаем ,тогда получаем , из которого находим функцию , из которого находим функцию 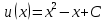 . . Следовательно, общее решение исходного уравнения имеет вид 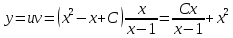 Пример 1. Решить дифференциальное уравнение 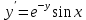 с начальным условием y(0)=0 с начальным условием y(0)=0 Решение. Заданное уравнение представляет собой дифференциальное уравнение 1-ого порядка с разделяющимися переменными. Проведём разделение переменных: 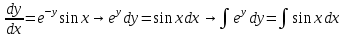 Находя интегралы, получим 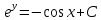 Решение можно оставить в неявном виде (в виде общего интеграла дифференциального уравнения). Здесь, однако, несложно выразить искомую функцию явно, т.е. получить общее решение дифференциального уравнения:  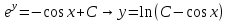 Для нахождения частного решения подставим начальное условие в найденное общее решение: 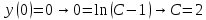 Тогда искомое частное решение 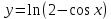 Пример 2. Решите уравнение 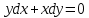 Решение. Имеем дифференциальное уравнение 1-ого порядка с разделяющимися переменными, записанное через дифференциалы. Разделение переменных даёт: 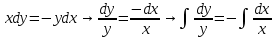 После интегрирования получаем  (Произвольная постоянная интегрирования здесь записана в логарифмическом виде для удобства дальнейших преобразований). 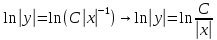 Отсюда находим общее решение уравнения 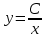 Задание 20. Найти частные производные и полный дифференциал а) 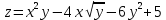 Решение: 1) Вычислим 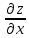 , при этом y считаем константой и выносим за знак производной: , при этом y считаем константой и выносим за знак производной: 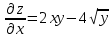 2) Вычислим 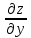 , при этом x считаем константой и выносим за знак производной: , при этом x считаем константой и выносим за знак производной: 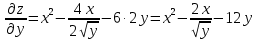 3) Вычислим 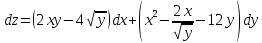 б) 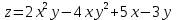 Решение: 1) Вычислим 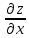 , при этом y считаем константой и выносим за знак производной: , при этом y считаем константой и выносим за знак производной: 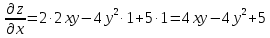 2) Вычислим 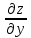 , при этом x считаем константой и выносим за знак производной: , при этом x считаем константой и выносим за знак производной: 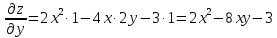 3) Вычислим 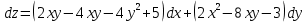 Задание 21. а) Найти первые четыре члена ряда по заданному общему члену: 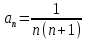 Решение: 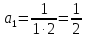 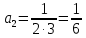 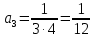 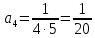 б) Найти первые три члена ряда по заданному общему члену: 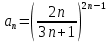 Решение: Подставляя в формулу общего члена последовательно n=1, 2, 3, 4 получим 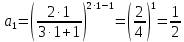 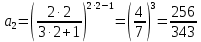 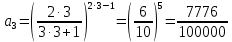 Задания контрольной работы Дано комплексное число z. Найти Re z, Imz, z, arg z, 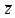 . Построить числа z и . Построить числа z и 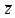 в одной системе координат. в одной системе координат.
|
