Методические рекомендации по выполнению контрольной работы по дисциплине Методы оптимизации
 Скачать 486 Kb.
|
|
Например, Задание 55 Ф = 4x1 + 5x2 → maх, 2  x1 + x2 ≥ 22x1 + 2x2≤ 20 1 ГРАФИЧЕСКИЙ СПОСОБ 1.1 Точки пересечения линий ограничений 2x1 + x2 = 22: x2 = 22 – 2x1: x1 = 0 → x2 = 22, x2 = 0 → x1 = 11; x1 + 2x2 = 20: x2 = ( 20 – x1 )/2: x1 = 0 → x2 = 10, x2 = 0 → x1 = 20. График  График с линиями ограничений 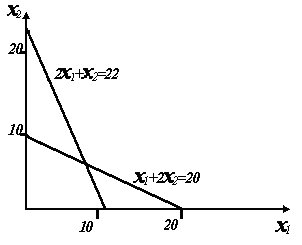 1.3 Многоугольник ограничений отметить стрелками т.к. 2x1 + x2 ³ 22, полуплоскость ниже этой линии т.к. x1 + 2x2£ 20, полуплоскость выше этой линии 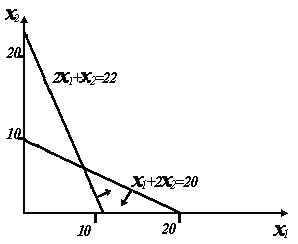 Пояснения: Так как точка (0,0) удовлетворяет рассматриваемому неравенству 2x1 + x2 ³ 22, приходим к выводу, что ограничению неравенства удовлетворяют точки полуплоскости, расположенные выше этой линии ограничений. Так как точка (0,0) не удовлетворяет рассматриваемому неравенству x1 + 2x2£ 20, приходим к выводу, что ограничению неравенства удовлетворяют точки полуплоскости, расположенные ниже этой линии ограничений. С учётом того, что x1 ³ 0 и x2³ 0, отмечаем область ограничений стрелками, указывающими направления, соответствующие полуплоскостям, в которых удовлетворяются ограничения. Максимум ЦФ в находится одной из угловых точек образовавшегося треугольника ограничений) 1.4 Линия уровня целевой функции, проходящая через точку (0,0): Ф = 4x1 + 5x2 = 0 Пояснение: подставив в выражение для линии уровня, например, x1 =5, получаем x2 = – 4x1 /5 = – 4·5/5 = – 4, то есть что рассматриваемая линия уровня проходит через точку (5, – 4) – проводим такую линию: 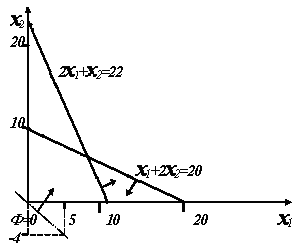 1.5 Провести линию уровня, соответствующую max, и найти maxФ Пояснения: Определяем в каком направлении необходимо перемещать линию уровня параллельно себе самой, чтобы значение Ф=0, чтобы значение ЦФ возрастало. Поскольку коэффициенты при x1 и x2 в выражении для целевой функции положительны, то увеличение Ф будет происходить при увеличении x1 и x2 , т.е. Ф необходимо перемещать вправо и вверх – см. график. очевидно, что в рассматриваемой области ограничений maxФ = Ф(20,0) = 4·20 + 5·0 = 8 – изобразить соответствующую линию уровня с указанием в выноске Ф =80. 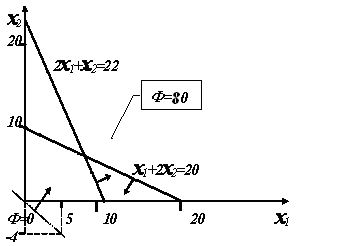  1.6 Решение для многоугольника ограничений, прилегающего к началу координат Запись ограничений: 2 x1 + x2 ≤22x1 + 2x2≤ 20 Для нахождения значения экстремума найдем координаты точки пересечения линий ограничения, записанных в виде 2x1 + x2 – 22 = 0 и x1 + 2x2– 20 = 0. Исходяиз того, что 2x1 + x2 – 22 =x1 + 2x2– 20 , в результате упрощения последнего равенства получаем x2=x1 – 2. Поставив x2=x1 – 2 в любое выражение для линии пересечения, получим 3x1 – 24 = 0, и, таким образом, координаты точки экстремума x1=8, x2=x1 – 2 = 6. Следовательно, в данном случае maxФ = Ф(8,6) = 4·8 + 5·6 = 62. Линии ограничений и линия уровня целевой функции, проходящая через точку (0,0) – прежние, однако многоугольник ограничений другой (отметим новыми малыми стрелками). Изобразим линию уровня, проходящую через точку экстремума, укажем на графическом изображении для линии уровня в выноску с надписью Ф =62  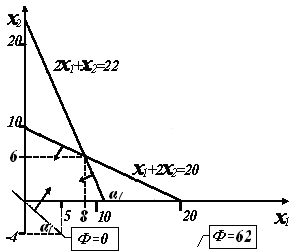 Определим координаты точек пересечения с осями линии уровня, соответствующей maxФ =62, воспользовавшись вычислениями с использованием tgα=  (см. рисунок).Как видно из рисунка, координаты точки пересечения линии уровняmaxФ =62 с осью x1 равны (8 + 6 / ,0) =(15 ,0),в то время как координаты точки пересечения с осью x2 (0,6+15  ,0) ==(0,12)2 АНАЛИТИЧЕСКОЕ РЕШЕНИЕ (решение для исходных ограничений) 2 x1 + x2 ≥22x1 + 2x2≤ 20 2.1 Получение и проверка базисного решения Приведём неравенства к равенствам (путём введения дополнительных переменных) 2 x1 + x2 – x3 = 22x1 +2x2 + x4 = 20 Найдем БР (в базисе дополнительных переменныхх3, х4 ) x3 = – 22 + 2x1 + x2x4 = 20 – x1 – 2x2 (при этом свободными являются переменные x1 и x2). Анализ БР не ДБР (вследствие наличия отрицательного свободного коэффициента во втором уравнении) 2.2 Приведение БР к ДБР всеми возможными попытками. Пояснение: при двух свободных переменных и двух уравнениях возможны 4 попытки. 1) перевод x1 в первом ур. (уравнении): x  3 = – 22 + 2x1 + x2 →x1 = ( 22 +x2 – x3)= 11 – x2 + x3x4 = 20–x1 – 2x2= 20 –(11 – x2 – x3)– 2x2 = 9 – x2 – x3ДБР (свободные коэффициенты неотрицательны во всех уравнениях). Проверка ДБР на оптимальность: выразим целевую функцию Ф = 4x1 + 5x2через свободные переменныеx2 и x3, принимая во внимание, что в ДБР x1 =11 – x2 + x3)Ф = 4(11 – x2 + x3)+5x2 = 4 x1+5 x2 =44+3x2 +2x3 .ДБР не оптимально (при поиске максимума свободные переменные со знаком +). 2) x2 в первом ур. x3 = – 22 + 2x1 + x2 → x2 = 22 – 2x1 + x3x4 =20–x1 – 2x2 = 20 – x1 – 2(22 – 2x1 + x3)=–24+3x1 –2x3 не ДБР (вследствие наличия отрицательного свободного коэффициента во втором уравнении). 3) x1 во втором ур. x 3 = – 22 + 2x1 + x2=22 +2(20 –2x2 – x4) + x2 = 18 – 3x2 – 2x4x4 = 20–x1 – 2x2 → x1 = 20 – 2x2 – x4 ДБР Проверка ДБР на оптимальность (выразим ЦФ Ф = 4x1 + 5x2через свободные переменные x1 и x3, принимая во внимание, что в ДБР x1 = 20 – 2x2 – x4) Ф = 4x1 + 5x2 =4(20 – 2x2 – x4) + 5x2 =80 – 3 x2 – 4x4 ДБР оптимально (при поиске максимума свободные переменные со знаками минус} maxФ =80 совпадает с графическим решением 4) x2 во втором ур.  x3 =–22 +2x1+x2=–22+2x1 +(10 – x1 – x4) =–12+ x1 – x4 x4 = 20–x1 – 2x2 → x2 = (20 – x1 – x4 )=10 – x1 – x4 |