Площадь криволинейной трапеции

• Название: Площадь криволинейной трапеции
• Дата: 08.02.2022
• Размер: 132.2 Kb.
• Имя файла: 7580a4dd5c9cb48ab13807c5dbacf0a8.docx
• Тип: Решение; #354602

Задания по теме «Площадь криволинейной трапеции»
Учитель математики

высшей квалификационной категории

МОУ Левобережной СОШ г.Тутаева

Борисова Елена Леонидовна

Пример 1

Найти площадь плоской фигуры, ограниченной линиями , .

Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы 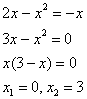 и прямой . Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:


Значит, нижний предел интегрирования , верхний предел интегрирования .
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:

А теперь рабочая формула: Если на отрезке 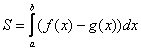 некоторая непрерывная функция больше либо равна некоторой непрерывной функции , то площадь фигуры, ограниченной графиками данных функций и прямыми , , можно найти по формуле:

В рассматриваемом примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из  необходимо вычесть

Завершение решения может выглядеть так:

Искомая фигура ограничена параболой  сверху и прямой  снизу.
На отрезке 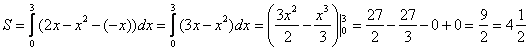  , по соответствующей формуле:


Ответ:

Пример 2

Вычислить площадь фигуры, ограниченной линиями , ,  , .

Решение: Сначала выполним чертеж: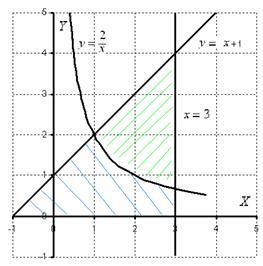


Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована зеленым цветом!

Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:

1) На отрезке  над осью  расположен график прямой ;

2) На отрезке  над осью  расположен график гиперболы .

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:



Ответ:

Пример 3

Вычислить площадь фигуры, ограниченной линиями: у = 4х – х2, у = 5, х = 3. Решение: х0 = 2, у0 = 4 Sф = SОАВД – SОСД Sпрям. = SОСД = F(3) – F(0), где F(x) первообразная для функции f(х) = 4х – х2 F(х)= ; SОСД= Sф = 15 – 9 = 6. Ответ: 6.

Пример 4

Вычислить площадь фигуры, ограниченной линиями ,

Решение:
Представим уравнения в «школьном» виде ,  и выполним поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: .
Но чему равен нижний предел?! Понятно, что это не целое число, но какое? Может быть ? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что . Или корень. А если мы вообще неправильно построили график?

В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.

Найдем точки пересечения прямой  и параболы .
Для этого решаем уравнение: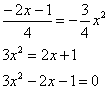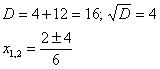


,

Действительно, .

Дальнейшее решение тривиально, главное, не запутаться в подстановках и знаках, вычисления здесь не самые простые.

На отрезке 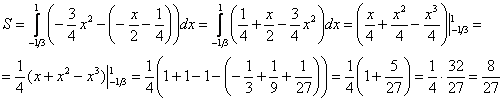   , по соответствующей формуле:


Ответ:

Пример 5

Вычислить S фигуры, ограниченной линиями у = (х + 2)², х = 0, у = 0.

Решение:

АОВ – криволинейный треугольник или криволинейная трапеция. (рис 10.)

S = F(0) – F(-2) = F(x) = x2 +4x+4; F(x) = S =

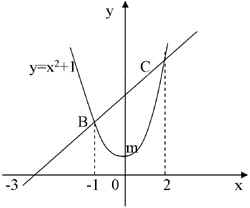
Ответ:

Пример 6

Найти S фигуры, ограниченной параболой у = х² + 1 и прямой у = х + 3.

Решение:

Построим в одной системе координат графики данных функций.

1) у = х² + 1, х₀ = 0, у₀ = 0.

х	-3	-2	-1	0	1	2	3
у	10	5	2	1	2	5	10

2) у = х + 3

3) х² + 1 = х + 3

х1 = 1, х2 =2. Sф = S1АВСД – S2АВmСД Sтр.АВСД = SАВmСД = F(2) – F(-1), F(x) = , S = 6 Sф = S1 – S2 = 4,5.

II способ.

S_АВСД = F(2) – F(-1), F(x) = .

Ответ: S_ф = 4,5.

Пример 7:

Найдите 3 четверти площади фигуры, ограниченной параболой, заданной уравнением у = – х2+4х-3 и осью абсцисс. Решение: 1) хВ=2, уВ=1 2) – х2+4х-3=0 х1=3, х2=1 Функция неотрицательна на [1;3] F(x) = Sф = F(3) – F(1) = 3) Умножим Sф на . Sиск.= Ответ: 1

Пример 8
Найти S фигуры, ограниченной линиями f₁(x) = x²; f₂(x) = 2x – x² .

Решение: 1) Схематично изобразим данную фигуру (рис. 12) f2(x) = – x2 + 2x х0 = , у0 = 1

2) Найдем абсциссы точек пересечения этих линий

х² = 2x – x²

2x² – 2х = 0

х = 0, х = 1

3) Найдем площадь фигуры

F₂(x) = x² –

S₂ = F(1) – F(0) =

F₁(x) = ; S₁ = .

4) S_ф = S₂ – S₁ = .

Ответ: S_ф = .
Пример 9

Вычислить S фигуры, ограниченной линиями: у=х3+1, у=0, х=0, х=2. Решение: F(x) = S = F(2) – F(0) = 16/4 + 2 – 0/4 + 0 = 6 Ответ: 6.

Пример 10

Вычислить площадь фигуры, ограниченной линиями , ,  и осью

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Что делать, если криволинейная трапеция расположена под осью ?

Решение:
Выполним чертеж: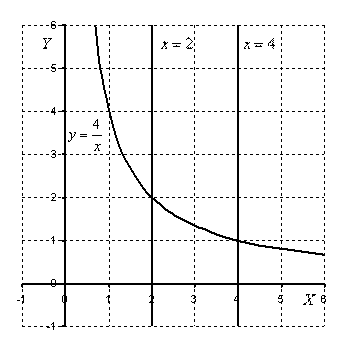

На отрезке   график функции  расположен над осью , поэтому:

Ответ:
Примечание: В задачах на нахождение площадей преподаватели часто требуют записывать ответ не только точно, но и, в том числе, приближенно.

Пример 11 : Найти площадь фигуры, ограниченной линиями ,

.Решение:
Выполним чертеж:

На отрезке  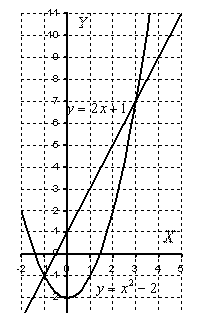  , по соответствующей формуле:

Ответ:

Пример 12:

Найти площадь фигуры, ограниченной линиями , .

Решение:
Выполним чертеж.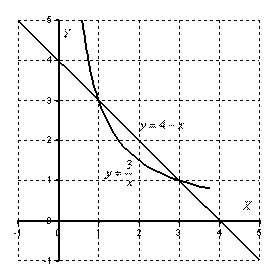

На отрезке 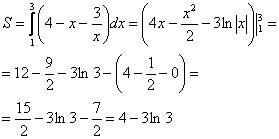   , по соответствующей формуле:

Ответ:

Используемые ресурсы:

1. 
   https://infourok.ru/samostoyatelnaya-rabota-po-teme-neopredelenniy-integral-klass-761699.html
   
2. 
   http://festival.1september.ru/articles/566339/
   
3. 
   http://school-collection.edu.ru/catalog/rubr/8a790bee-ba9d-4b2b-9c3a-6e370cc2df5b/113019/?
   
4. 
   ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)
   
5. 
   Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России