Пример решения контрольной работы
Задание № 1
Задание 55: f(x,y)=2x3+xy2+5x2+y2
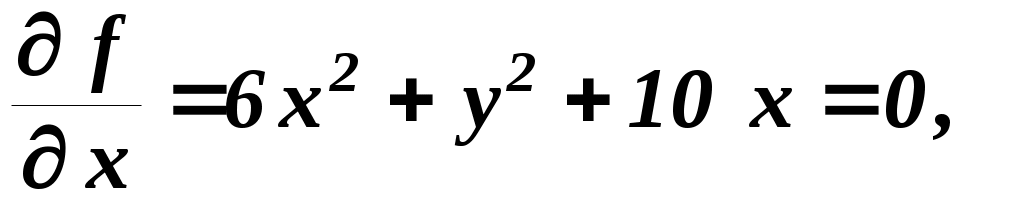 (1) (1)
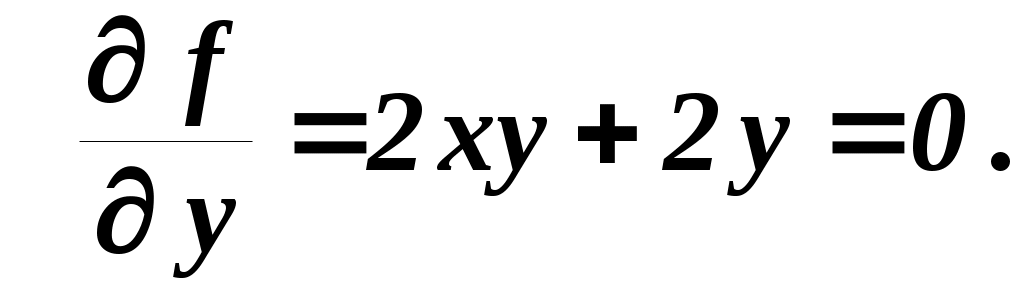 (2) (2)
Из (2) 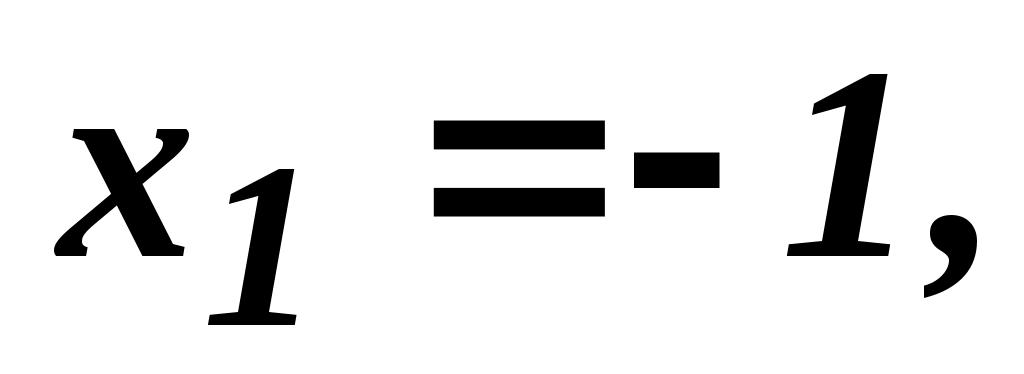 либо либо 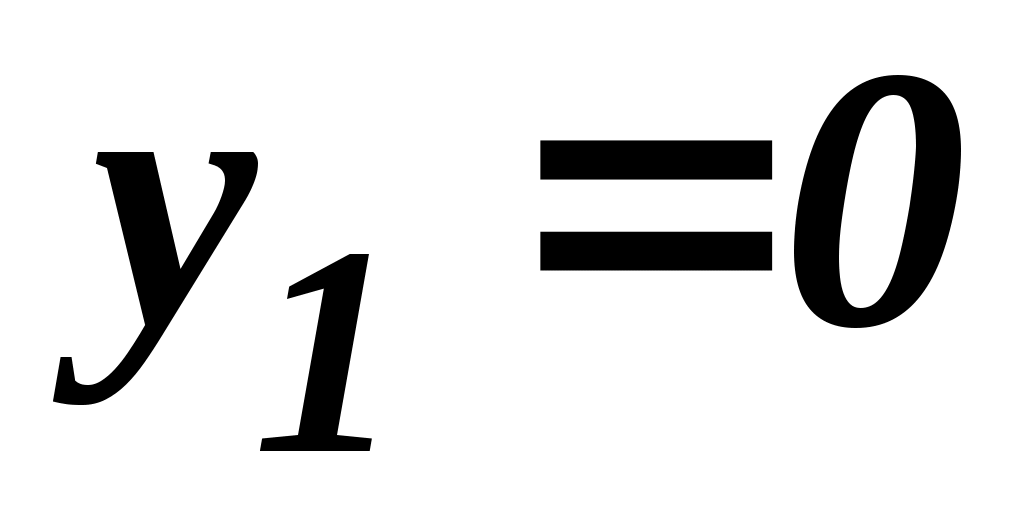
Из (3):
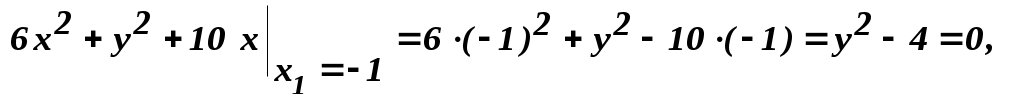
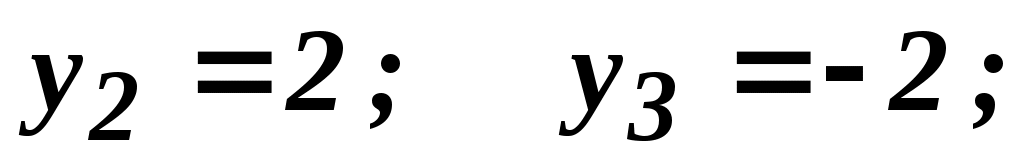
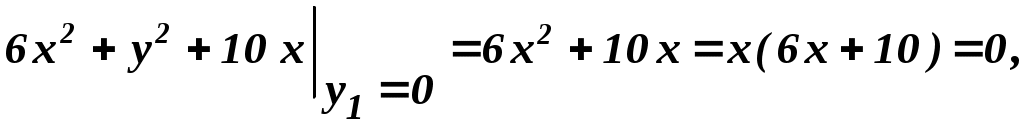
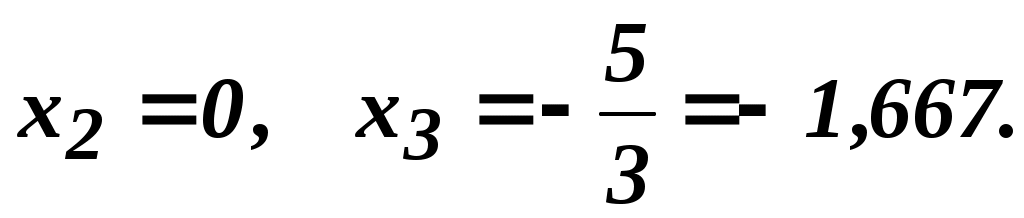
Проверка: 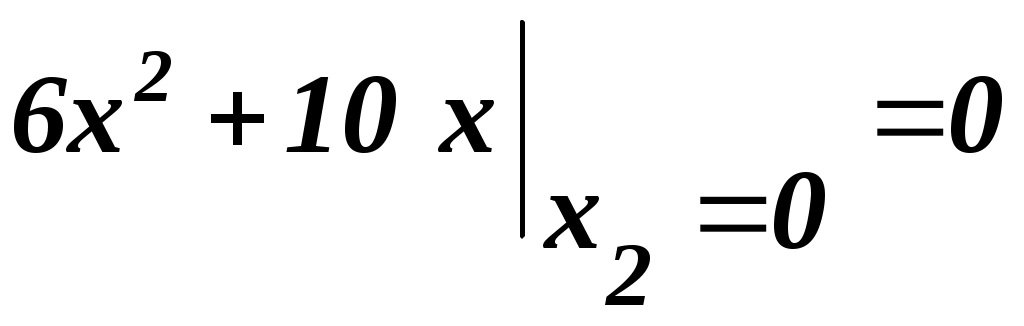 ; ;
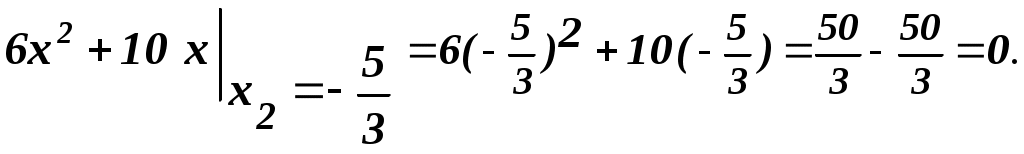

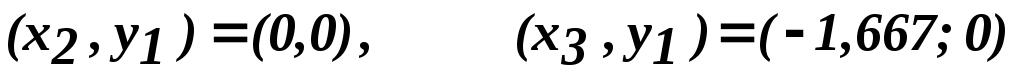
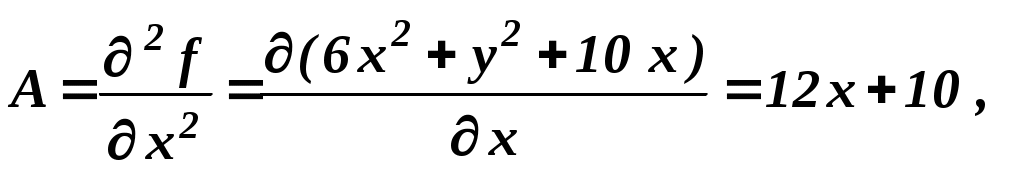 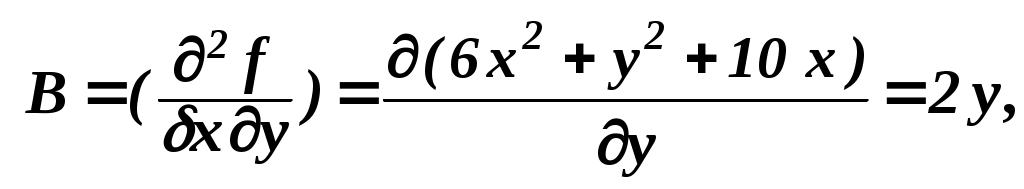
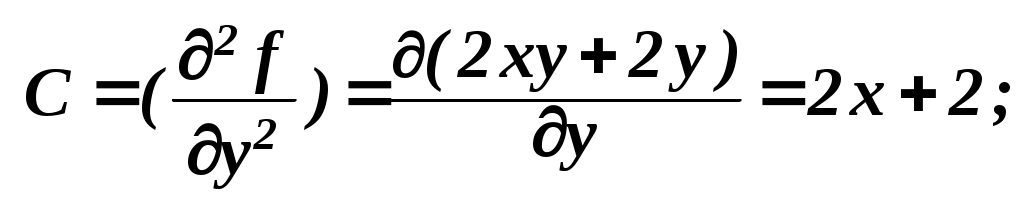
(0,0):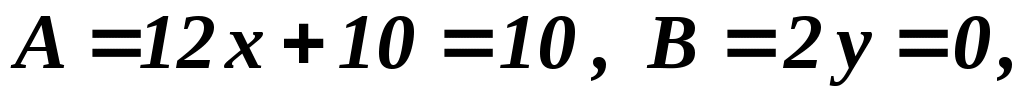 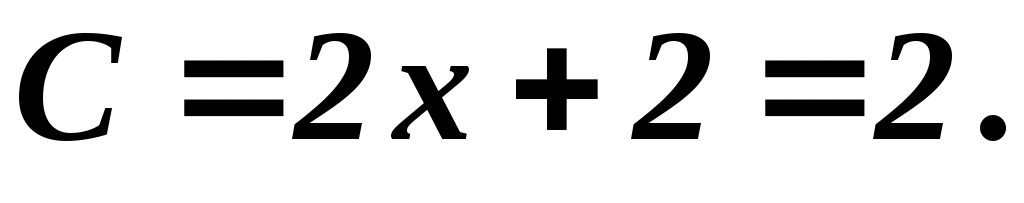
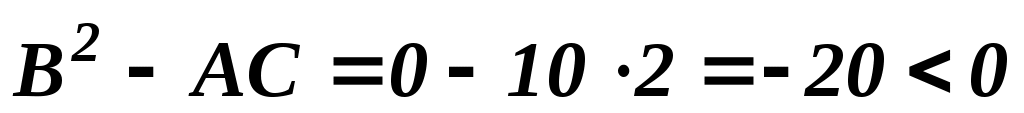 экстремум, экстремум,
А и С положительны – минимум
f(0,0) = 0;
(–1,667;0):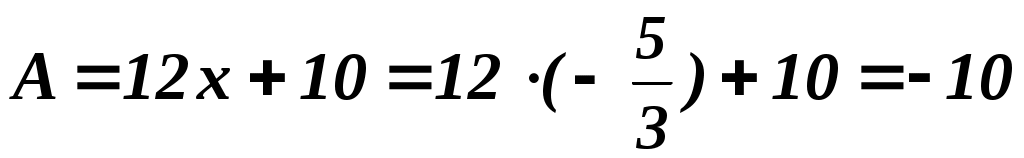 , , 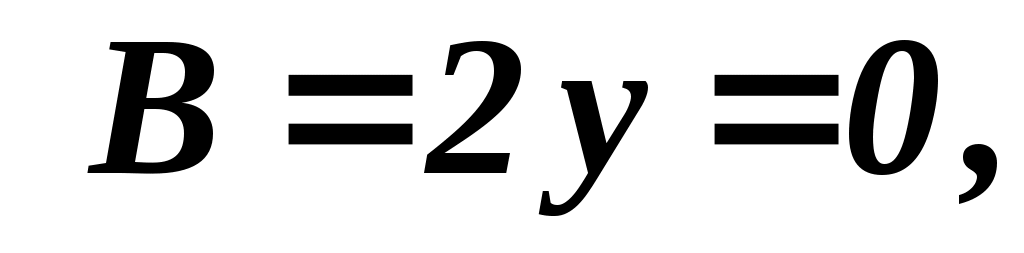
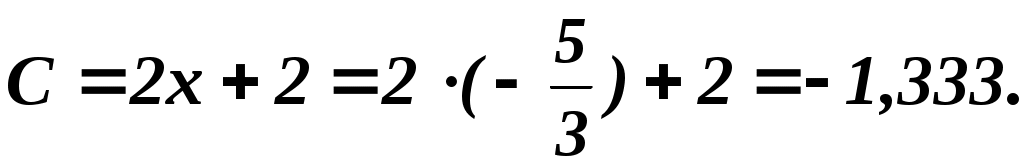
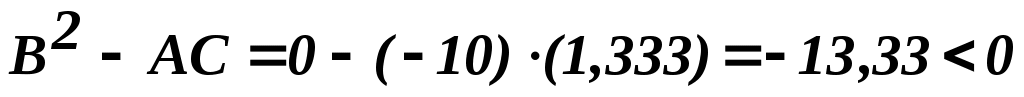 , экстремум, А и С отрицательны – максимум , экстремум, А и С отрицательны – максимум
f(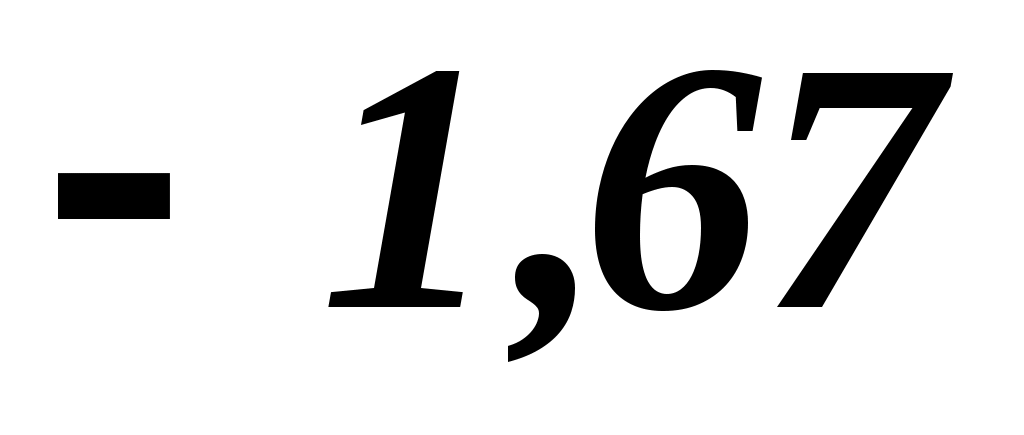 ;0)= 2 ;0)= 2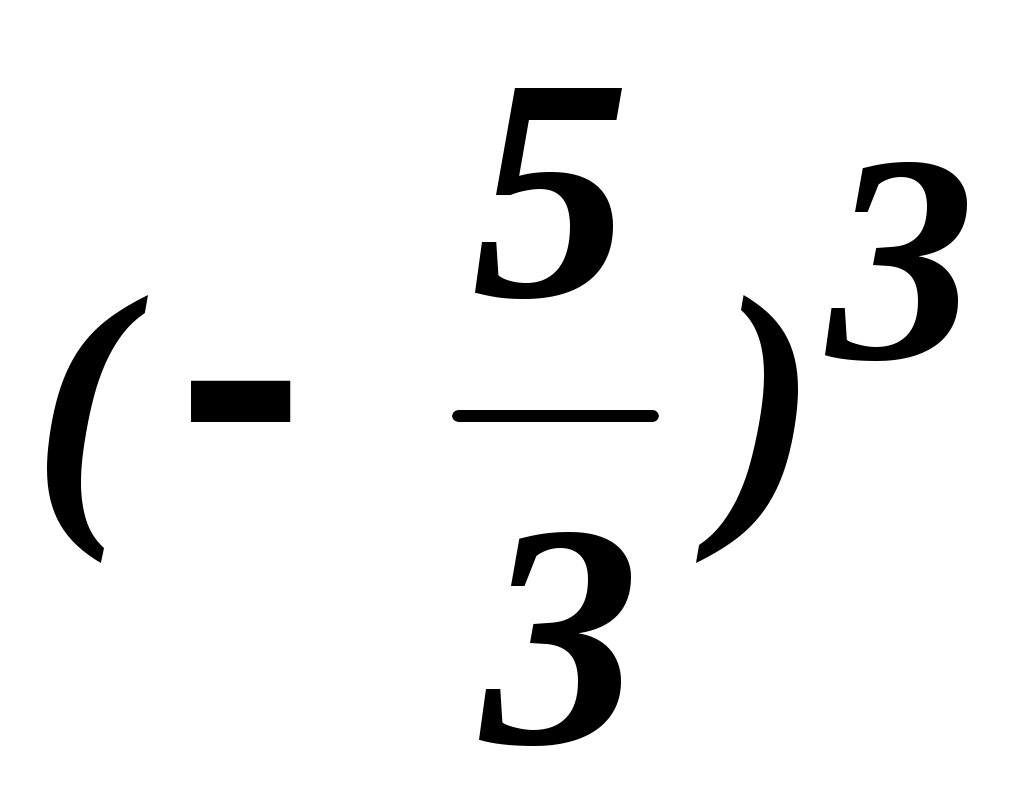 +5 +5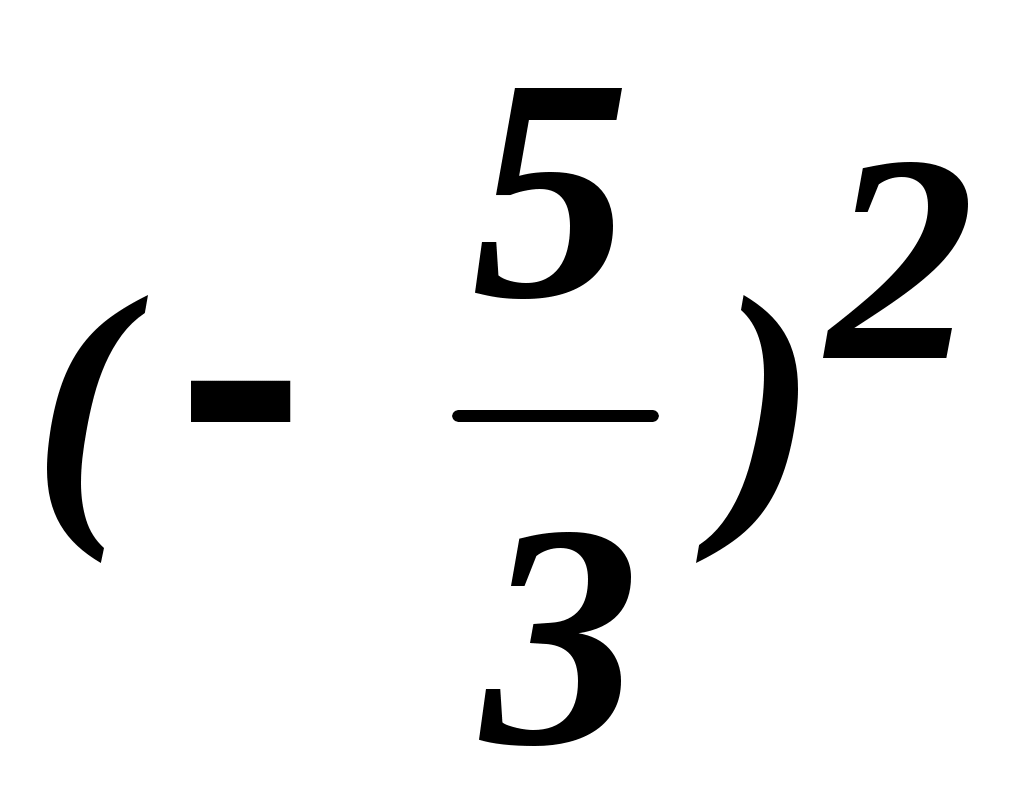 = 4,630; = 4,630;
(-1,2): 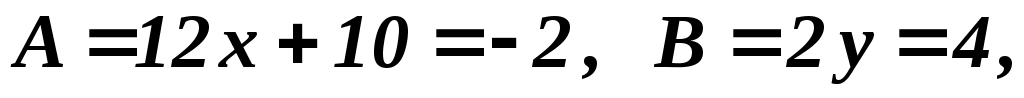 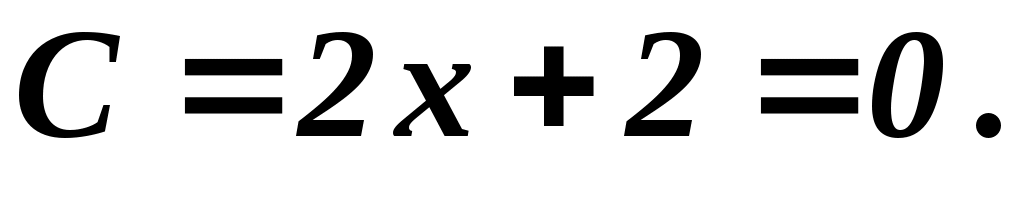
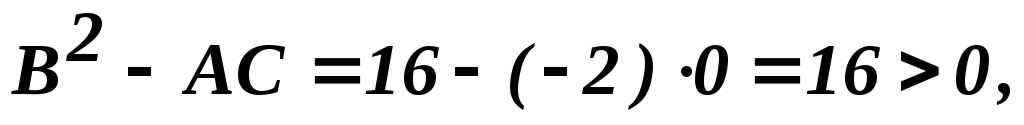 не экстремум не экстремум
f(–1,2) = 2x3+xy2+5x2+y2 = 3;
(–1,–2): 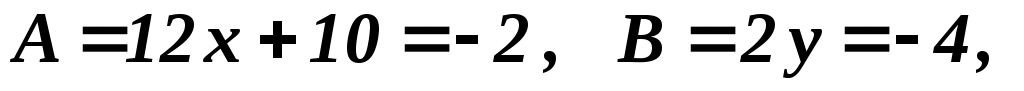
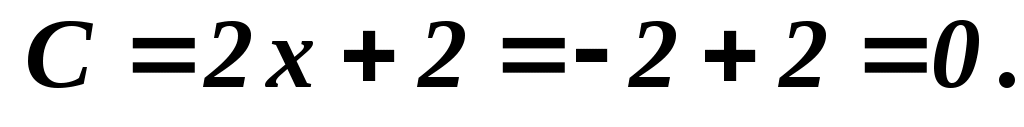
 не экстремум не экстремум
f(–1, –2) = 2x3+xy2+5x2+y2 = 3.
Задание № 2
«РЕШЕНИЕ ЗАДАЧИ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ГРАФИЧЕСКИ И АНАЛИТИЧЕСКИ»
(методические указания)
Цель контрольной работы: исследование способов решения задачи линейного программирования
Задача: Найти максимум целевой функции Ф = k1 x1+ k2 x2 при ограничениях ( - один из знаков ≤ , ≥) - один из знаков ≤ , ≥)
a 11x1 + a12x2 11x1 + a12x2  b1 , a21x1 + a22x2 b1 , a21x1 + a22x2  b2 , b2 ,
1 ГРАФИЧЕСКИЙ СПОСОБ
1.1 Вычислить точки пересечения линий ограничений с осями декартовой системы координат.
1.2 Построить график с изображением линий ограничений в декартовой системе координат.
1.3 Определить многоугольник ограничений
1.4 Построить линию уровня целевой функции, проходящую через точку (0,0)
1.5. Провести линию уровня, соответствующую max, и найти значение экстремума целевой функции (ЦФ)
1.6. Записать ограничения и найти значение экстремума для многоугольника ограничений, прилегающего к началу координат, а также координаты точек пересечения с осями линии уровня, соответствующей max.
2 АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
6. Найти решение для исходных ограничений задачи, используя способ перевода свободной переменной в базисные со всеми возможными попытками получения ДБР.
Примечание: числа, не являющиеся целыми, представлять правильными дробями
Варианты задания 2
1
|
maxФ = 7 x1 + 8 x2
|
5 x1 + 2 x2 ≤ 40
|
x1 + 2 x2≥16
|
2
|
maxФ = 6 x1 + 7 x2
|
5 x1 + 2 x2 ≥ 40
|
x1 + 2 x2≤16
|
3
|
maxФ = 6 x1 + 5 x2
|
2 x1 + x2 ≤ 16
|
2x1 + 5 x2≥40
|
4
|
maxФ = 5 x1 + 4 x2
|
2 x1 +2 x2 ≥ 16
|
2x1 + 5x2≤40
|
5
|
maxФ = 3 x1 +2 x2
|
3x1 + x2 ≤ 18
|
2x1 +5 x2≥ 60
|
6
|
maxФ = 6 x1 + 4 x2
|
3x1 + x2 ≥ 18
|
4x1 + 6x2≤ 60
|
7
|
maxФ = 5 x1 + 4 x2
|
2x1 + x2≤14
|
x1 + 3 x2≥18
|
8
|
maxФ = 4 x1 + 5 x2
|
2x1 + x2≥10
|
x1 +3 x2≤18
|
9
|
maxФ = 6 x1 + 8 x2
|
9 x1 + 5 x2 ≤ 90
|
3 x1 + 5 x2≥ 60
|
10
|
maxФ = 5 x1 + 7 x2
|
9 x1 + 5 x2 ≥ 90
|
3 x1 + 8x2≤ 60
|
11
|
maxФ = 6 x1 + 7 x2
|
5 x1 + 3 x2 ≤ 60
|
5 x1 + 9 x2≥ 90
|
12
|
maxФ = 5 x1 + 6 x2
|
5 x1 + 3 x2 ≥ 60
|
5 x1 + 9 x2≤ 90
|
13
|
maxФ = 5 x1 + 5 x2
|
3 x1 +2 x2 ≤ 30
|
x1 + 4 x2≥ 20
|
14
|
maxФ = 3 x1 + 3 x2
|
3 x1 +2 x2 ≥ 30
|
x1 + 4 x2≤ 20
|
15
|
maxФ = 2 x1 + 7 x2
|
4 x1 + x2 ≤ 20
|
2 x1 + 3 x2≥ 30
|
16
|
maxФ = 6 x1 + 5 x2
|
4 x1 + x2 ≥ 20
|
2 x1 + 3 x2≤ 30
|
17
|
maxФ = 5 x1 + 4 x2
|
2 x1 + x2 ≥ 22
|
x1 + 2x2≤ 20
|
18
|
maxФ = 10 x1 + 8 x2
|
2 x1 + x2 ≤ 20
|
x1 + 2x2≥ 18
|
19
|
maxФ = 4 x1 + 5 x2
|
2 x1 + x2 ≥ 20
|
x1 + 2x2≤ 18
|
20
|
maxФ = 7 x1 + 8 x2
|
5 x1 + 2 x2 ≤ 40
|
x1 + 2 x2≥16
|
21
|
maxФ = 6 x1 + 7 x2
|
5 x1 + 2 x2 ≥ 40
|
x1 + 2 x2≤16
|
22
|
maxФ = 5 x1 + 3 x2
|
3 x1 + x2 ≤ 18
|
x1 + 3 x2≥ 20
|
23
|
maxФ = 5 x1 + 4 x2
|
3 x1 + x2 ≥ 15
|
x1 + 3 x2≤ 18
|
24
|
maxФ = 6 x1 +4 x2
|
3x1 + x2 ≤ 18
|
x1 + x2≥10
|
25
|
maxФ = 5 x1 + 4 x2
|
3x1 + x2 ≥ 18
|
x1 + x2≤10
|
26
|
maxФ = 5 x1 + 3 x2
|
4 x1 + 5x2≤ 80
|
x1 + 3 x2≥18
|
27
|
maxФ = 4 x1 + 5 x2
|
4 x1 + x2≥ 40
|
x1 +3 x2≤18
|
28
|
maxФ = 6 x1 + 8 x2
|
9 x1 + 5x2 ≤ 90
|
3 x1 + 5 x2≥ 60
|
29
|
maxФ = 8 x1 + 7 x2
|
9 x1 + 5 x2 ≥ 90
|
3 x1 + 5x2≤ 60
|
30
|
maxФ = 6 x1 + 3 x2
|
6 x1 +5 x2 ≤ 90
|
2 x1 + 4 x2≥ 40
| |
 Скачать 486 Kb.
Скачать 486 Kb.
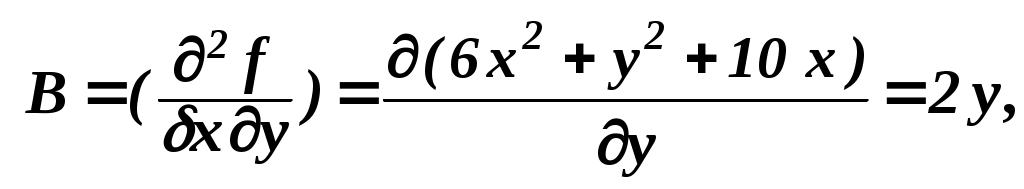
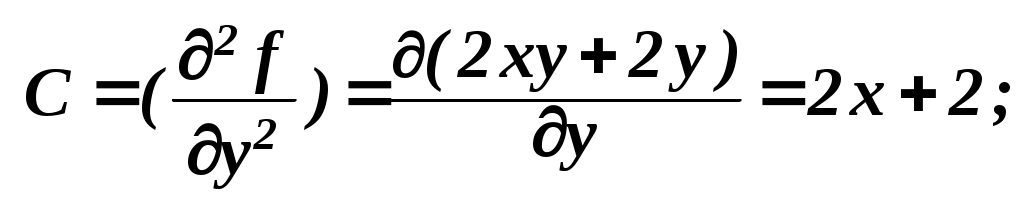
 11x1 + a12x2
11x1 + a12x2 