Методические рекомендации по выполнению контрольной работы по дисциплине Методы оптимизации
 Скачать 486 Kb.
|
|
не ДБР (вследствие наличия отрицательного свободного коэффициента в первом уравнении). Пример оформления контрольной работы Задании № 2 Вариант 55 Ф = 4x1 + 5x2 → maх, 2  x1 + x2 ≥ 22x1 + 2x2≤ 20 ГРАФИЧЕСКИЙ СПОСОБ Для исходных ограничений 2x1 + x2 = 22: x2 = 22 – 2x1: x1 = 0 → x2 = 22 x2 = 0 → x1 = 11 x1 + 2x2 = 20: x2 = ( 20 – x1 )/2: x1 = 0 → x2 = 10 x2 = 0 → x1 = 20 2x1 + x2 £ 22, полуплоскость ниже линии x1 + 2x2³ 20, полуплоскость выше линии 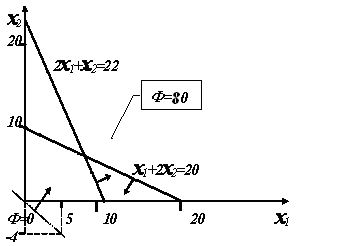  Линия уровня x1 =5, x2 = – 4x1 /5 = – 4·5/5 = – 4 maxФ = Ф(20,0) = 4·20 + 5·0 = 80 Для многоугольника ограничений, прилегающего к началу координат Запись ограничений: 2 x1 + x2 ≤22 x1 + 2x2≤ 20 Линии ограничения: 2x1 + x2 – 22 = 0 x1 + 2x2– 20 = 0 (1) 2x1 + x2 – 22 =x1 + 2x2– 20 , x2=x1 – 2. Подставим в (1): x1 + 2(x1 – 2) – 20 = 0, x1=8 maxФ = Ф(8,6) = 4·8 + 5·6 = 62.  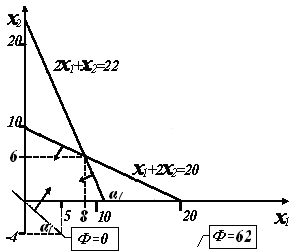 tgα=  (8 + 6/ ,0) =(15 ,0),(0,6+15  ,0) ==(0,12)АНАЛИТИЧЕСКОЕ РЕШЕНИЕ для исх. огр.
x3 = 22 – 2x1 – x2x4 = – 20 + x1 + 2x2 не ДБР 1) x1 в первом ур. x  3 = – 22 + 2x1 + x2 →x1 = ( 22 +x2 – x3)= 11 – x2 + x3x4 = 20–x1 – 2x2= 20 –(11 – x2 – x3)– 2x2 = 9 – x2 – x3ДБР Ф = 4(11 – x2 + x3)+5x2 = 4 x1+5 x2 =44+3x2 +2x3ДБР не оптимально – свободные переменные со знаком +. 2) x2 в первом ур. x3 = – 22 + 2x1 + x2 → x2 = 22 – 2x1 + x3x4 =20–x1 – 2x2 = 20 – x1 – 2(22 – 2x1 + x3)=–24+3x1 –2x3 не ДБР 3) x1 во втором ур. x 3 = – 22 + 2x1 + x2= 22 +2(20 –2x2 – x4) + x2 = 18 – 3x2 – 2x4x4 = 20–x1 – 2x2 → x1 = 20 – 2x2 – x4 ДБР Ф = 4x1 + 5x2 =4(20 – 2x2 – x4) + 5x2 =80 – 3 x2 – 4x4 оптиум – свободные переменные со знаками минус. maxФ =80 совпадает с графическим решением 4) x2 во втором ур.  x3 =–22 +2x1+x2=–22+2x1 +(10 – x1 – x4) =–12+ x1 – x4 x4 = 20–x1 – 2x2 → x2 = (20 – x1 – x4 )=10 – x1 – x4не ДБР |