Гидравлика. Сборник лабораторных работ. Методические указания дл. Методические указания для студентов очного обучения направления 551800 технологические машины и оборудование
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
УКАЗАНИЯ К выполнению работыЗадачи данного раздела можно решать без записи уравнения Бернулли. Так, если дана задача на истечение через отверстие, насадок или дроссель (жиклер) и задан коэффициент расхода Следует знать, что коэффициент расхода Указанное выше основное выражение для расхода справедливо при истечении через отверстия, насадки и дроссели. Последние могут иметь форму отверстия или насадка, но всегда истечение через них происходит в среду, заполненную той же самой жидкостью (истечение под уровень). При этом кинетическая энергия, теряемая на вихрообразования, учитывается коэффициентом расхода. Если истечение жидкости происходит при переменном напоре (опорожнение резервуаров), то в каждый данный момент движение жидкости можно рассматривать как установившееся.
выводы по работе.3. Объекты и средства выполнения работыОбъектом исследования является цилиндрическая оболочка с жидкостью, имеющая насадок диаметром d основные параметры которой приведены в таблице 1. Для выполнения работы студент должен иметь линейку, карандаш, лист миллиметровой бумаги, ПЭВМ. 4. Задание на работу
Примечание. Во всех вариантах расчета геометрические параметры сосуда, приведенные в табл. 1 увеличить в 100 раз. 5. Порядок выполнения работы
6. Отчет по работеОтчёт по работе должен включать :
ЛАБОРАТОРНАЯ РАБОТА №31. Цель и задачи работыЦель работы—изучение теоретических основ гидродинамики применительно к исследованию истечения жидкости через профилированные насадки. 2. Основные теоретические положения При решении некоторых простейших задач о движении жидкостей часто в первом приближении делают допущение о том, что движущаяся жидкость является идеальной. Под идеальной понимают жидкость, лишенную перечисленных выше свойств, т. е. жидкость абсолютно несжимаемую и нерасширяемую, не способную сопротивляться растяжению и сдвигу, а также лишенную свойства испаряемости ( Следовательно, в движущейся идеальной жидкости возможен лишь один вид напряжений — напряжение сжатия, т. е. давление Уравнение расхода представляет собой условие неразрывности (сплошности) потока несжимаемой жидкости, или, что то же самое, равенство объемных расходов в каких-то двух поперечных сечениях одного и того же потока, например 1 и 2,т.e. т. е. скорости обратно пропорциональны площадям поперечных сечений потоков. При этом предполагается, что скорость во всех точках данного сечения одинакова. Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Под удельной понимают энергию, отнесенную к единице веса, объема или массы жидкости. Обычно удобнее бывает относить энергию к единице веса. В этом случае уравнение Бернулли, записанное для сечений 1 и 2 элементарной струйки или потока идеальной жидкости имеет вид где Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение (2.2) примет вид, которым также часто пользуются: Если же энергию жидкости отнести к единице массы, то можно получить 3-ю формулу записи уравнения (2.2): Для потока реальной (вязкой) жидкости уравнение Бернулли следует писать в таком виде: где Различают два вида гидравлических потерь напора: местные потери и потери на трение по длине. Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется — расширяется, сужается, искривляется — имеет место более сложная деформация. Местные потери выражают формулой Вейсбаха где Числовое значение коэффициента Здесь Число Рейнольдса определяет режим движения жидкостей (и газов) в трубах. При При Можно считать, что при турбулентном режиме коэффициенты местных сопротивлений где А — число, определяемое формой местного сопротивления; где 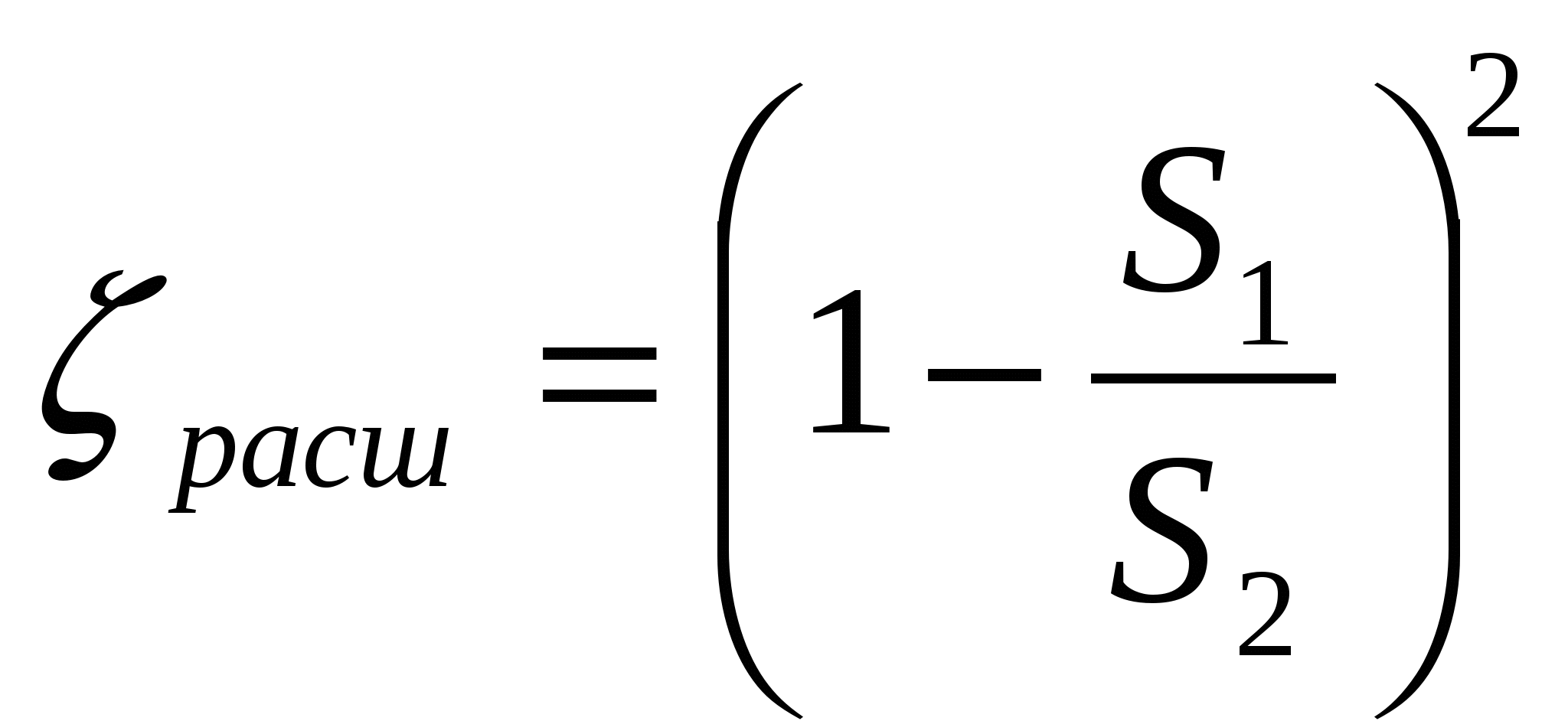 , (2.8) , (2.8)где При внезапном сужении трубы без закругления коэффициент сопротивления определяют по формуле Идельчика где Коэффициенты сопротивлений для постепенно расширяющихся (конических) труб — диффузоров, плавно сужающихся труб — сопл, поворотов и других, более сложных местных. гидравлических сопротивлений (кранов, фильтров и т. п.) - находят в справочной литературе. В задачах данного сборника коэффициенты Потери напора на трение по длине где безразмерный коэффициент сопротивления трения при ламинарном режиме при турбулентном режиме (Подробнее об этом см. в гл. 4.) Распределение скоростей по поперечному сечению круглой трубы радиусом причем максимальная скорость на оси трубы в два раза больше средней. При ламинарном течении в зазоре где число Рейнольдса Формула (2.13) справедлива также для зазора, образованного двумя соосными цилиндрическими поверхностями при условии, что зазор При ламинарном течении в трубке квадратного сечения вместо (2.11) и (2.13) можно принимать Частный случай течения жидкости (газа) через профилированный насадок. Во многих случаях приходится встречаться с движением газа с большими скоростями (например, в ракетной технике, в газовых турбинах и т. д.). Физический процесс таких течений очень сложен. Рассмотрим лишь одну характерную особенность течения газа с большой скоростью по трубам переменного сечения, заключающуюся в том, что скорость газа с увеличением площади сечения трубопровода не всегда убывает, как то имеет место при движении несжимаемой жидкости, а может и возрастать (если скорость газа превышает скорость звука). Рассмотрим этот вопрос более подробно. Как известно, при движении несжимаемой жидкости по трубе переменного диаметра d, а следовательно, и переменной площади поперечного сечения S средняя скорость в соответствии с уравнением сплошности увеличивается с уменьшением d (т.е. с уменьшением S), и, наоборот, уменьшается с увеличением d.(рис. 1). 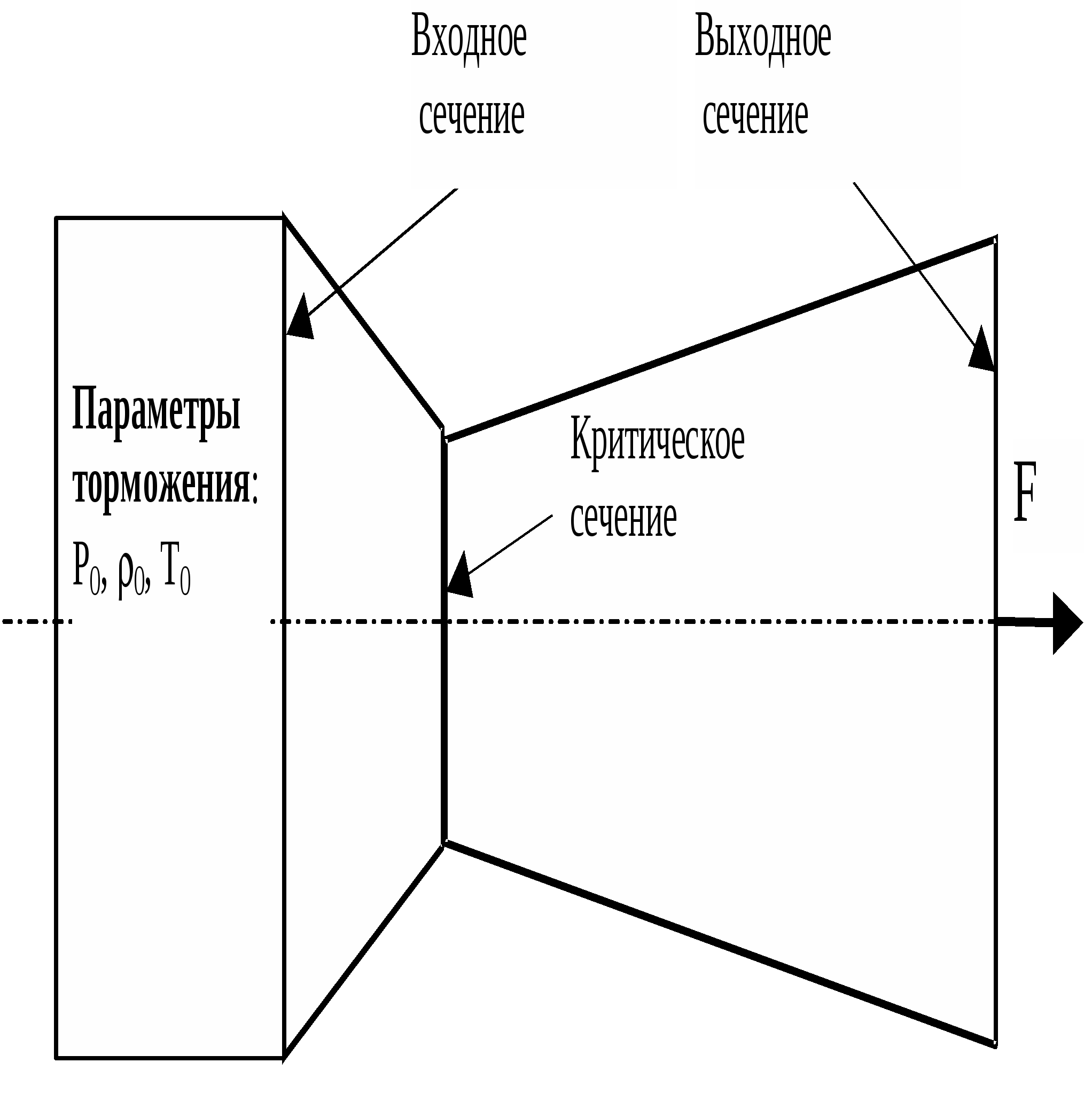 Рис. 1 Сопло Лаваля При движении газа такое соотношение может и не сохраниться. Рассмотрим, например, случай установившегося движения невязкой газообразной жидкости. По условию постоянства массового расхода вдоль трубопровода (уравнение неразрывности) и, разделив его на произведение , найдем откуда следует Определим теперь, чему равно Если для упрощения задачи принять трубу горизонтальной, то z=const и dz=0. В этом случае уравнение Бернулли упрощается: откуда Делая подстановку в (*), найдем 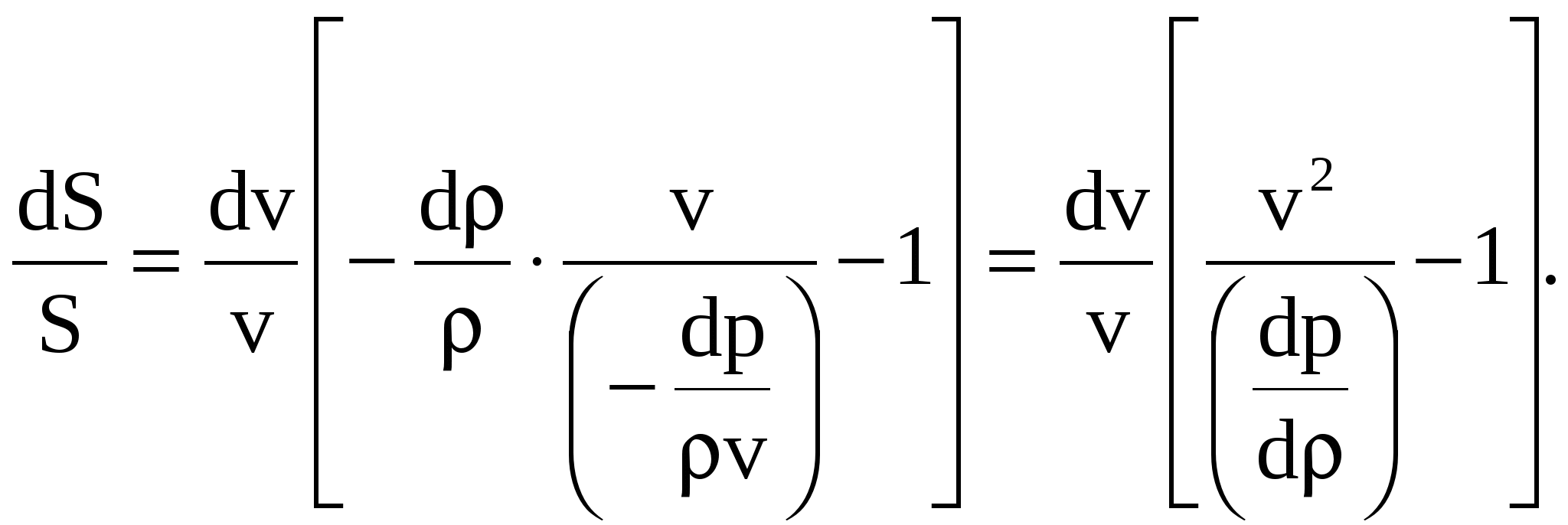 Учитывая, что для изоэнтропийного процесса местная скорость звука равна где: М — число Маха. Это уравнение показывает, что поток ускоряется вдоль канала переменного сечения ( Таким образом, для непрерывного увеличения скорости газа необходимо сначала сужать дозвуковой поток, пока скорость не достигает скорости звука, а затем расширять сечение сверхзвукового потока. В узком сечении сопла, где М = 1, величина Система уравнений, описывающих одномерное установившееся изоэнтропическое движение газа в канале переменного сечения, включают следующие зависимости: уравнение неразрывности G = VS , уравнение Бернулли уравнение адиабаты где P, , i, V, G — давление, плотность, полная энтальпия, скорость и расход газа в некотором сечении канала; Для перевода газа из состояния покоя в движение со скоростью V, необходимо израсходовать часть его энтальпии равную: где i0 = CрТ0, i = CрТ. Здесь и далее индексом “0” отмечены параметры торможения. Деля обе части уравнений (1) на квадрат скорости звука с2=RT и учитывая, что Принимая во внимание, что Или 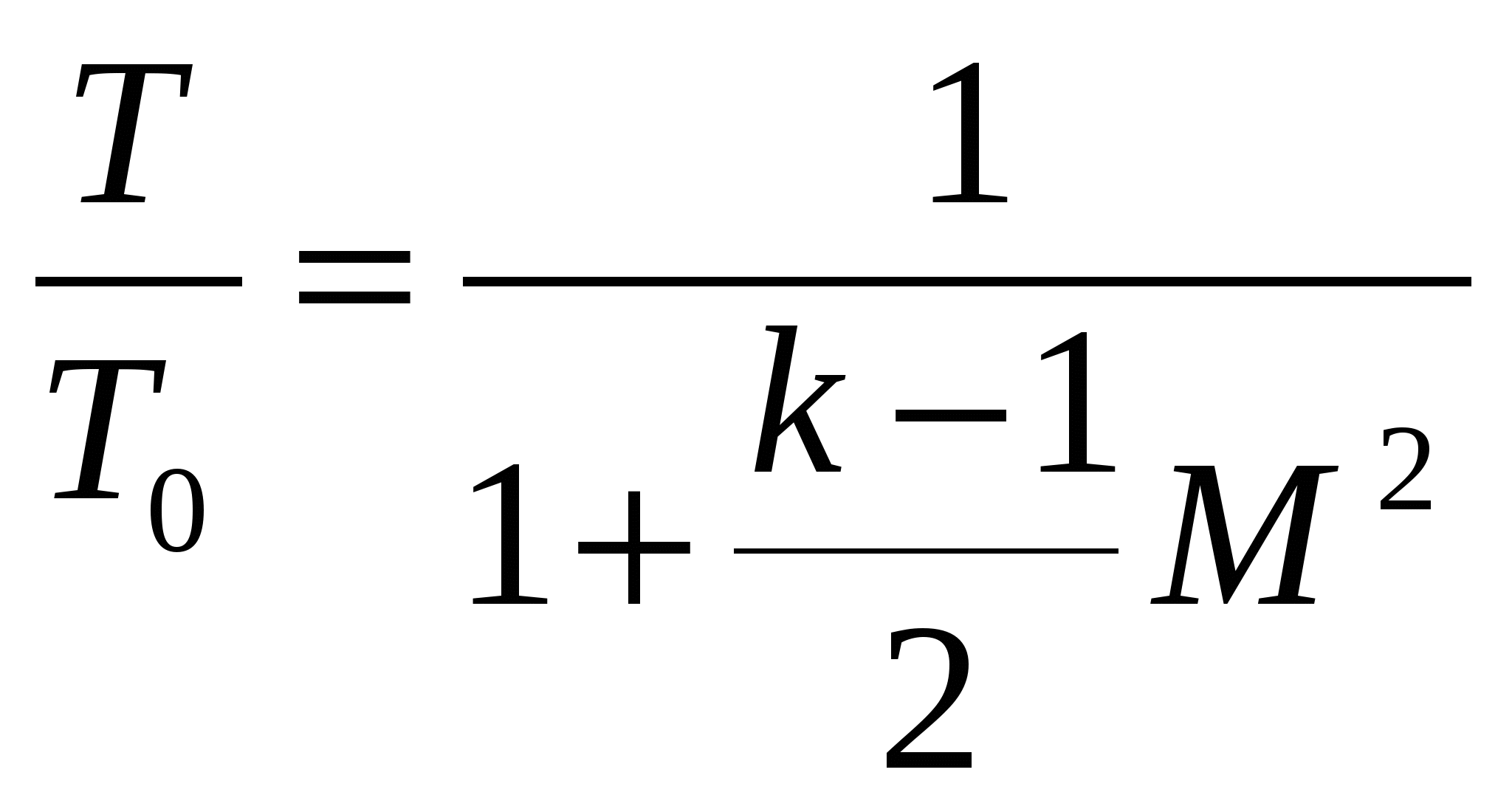 (2) (2)Пользуясь соотношениями для идеальной адиабаты: можно получить формулы для вычисления давления и плотности в идеальном потоке через параметры торможения: 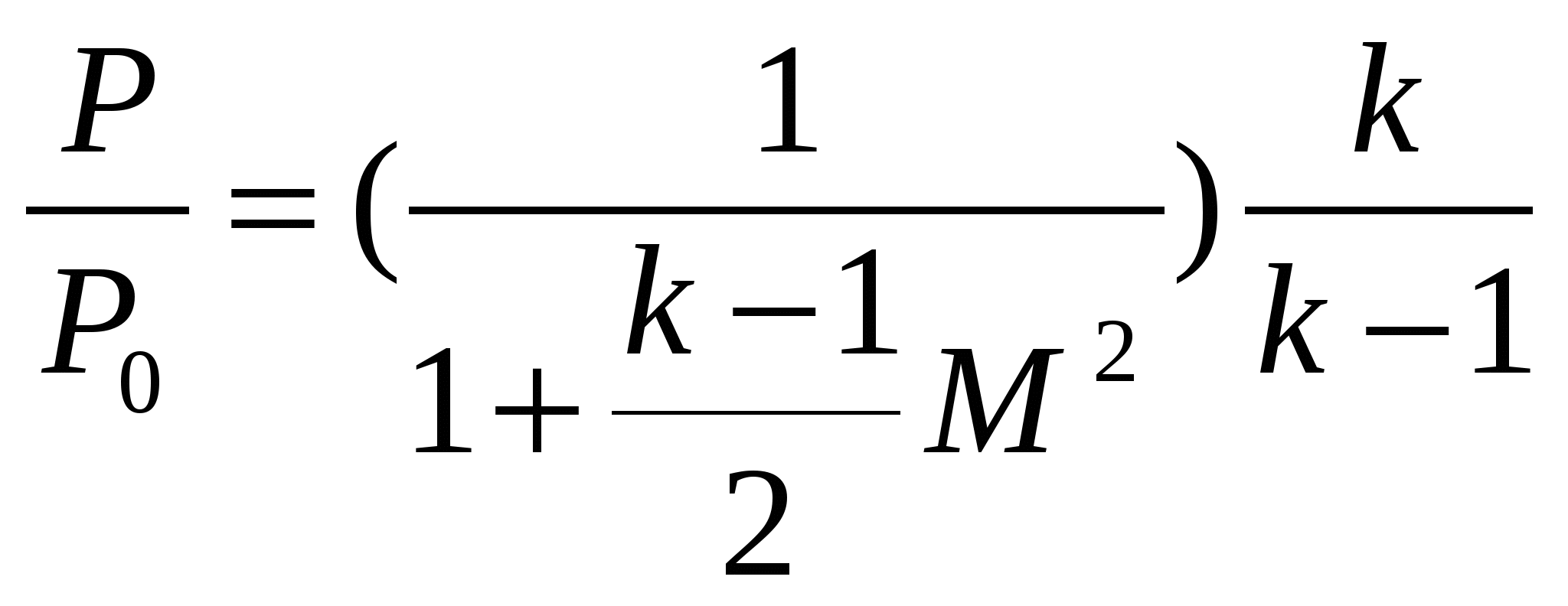 (3) (3)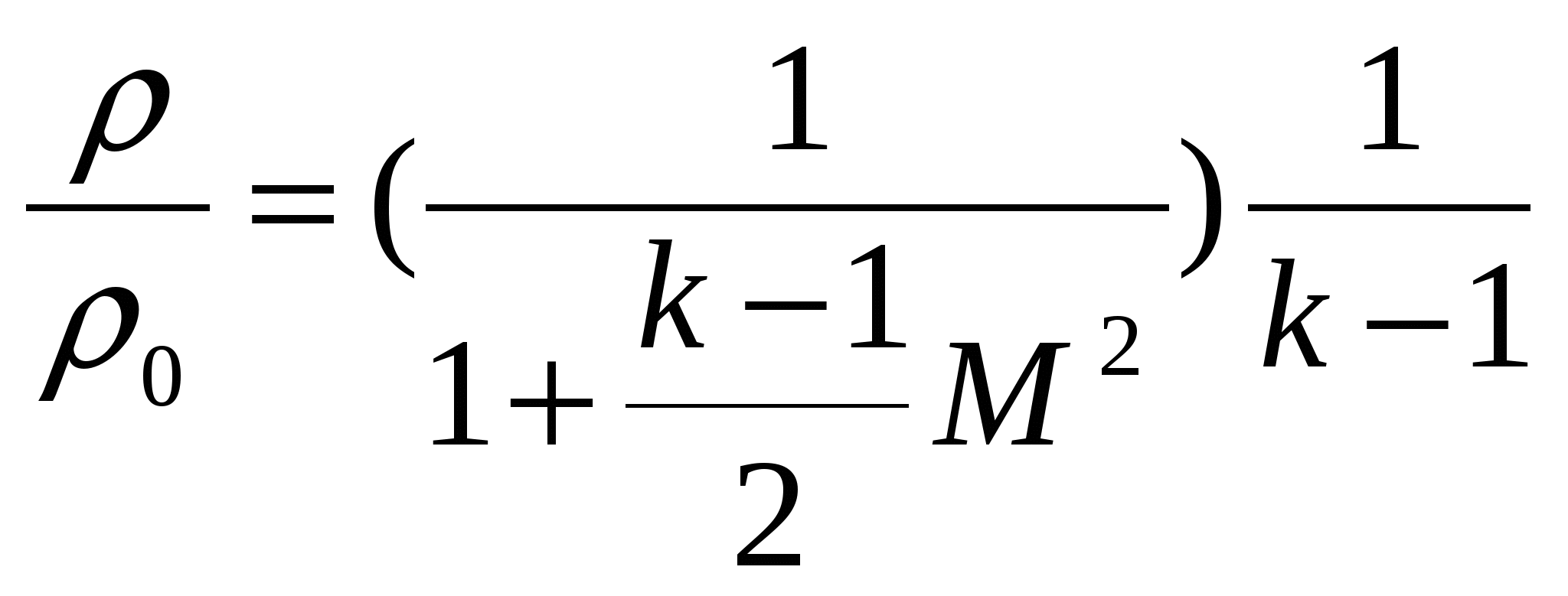 (4) (4)В критическом режиме скорость течения газа равна скорости звука и из уравнений (2), (3), (4) можно получить следующие выражения для критических значений параметров газа: Отсюда также следует, что скорость звука в критическом режиме течения определяется по формуле: Можно характеризовать степень преобразования энтальпии в кинетическую энергию ещё одним способом. Разделив уравнение (1) на квадрат критической скорости звука и вводя понятие приведённой скорости газа 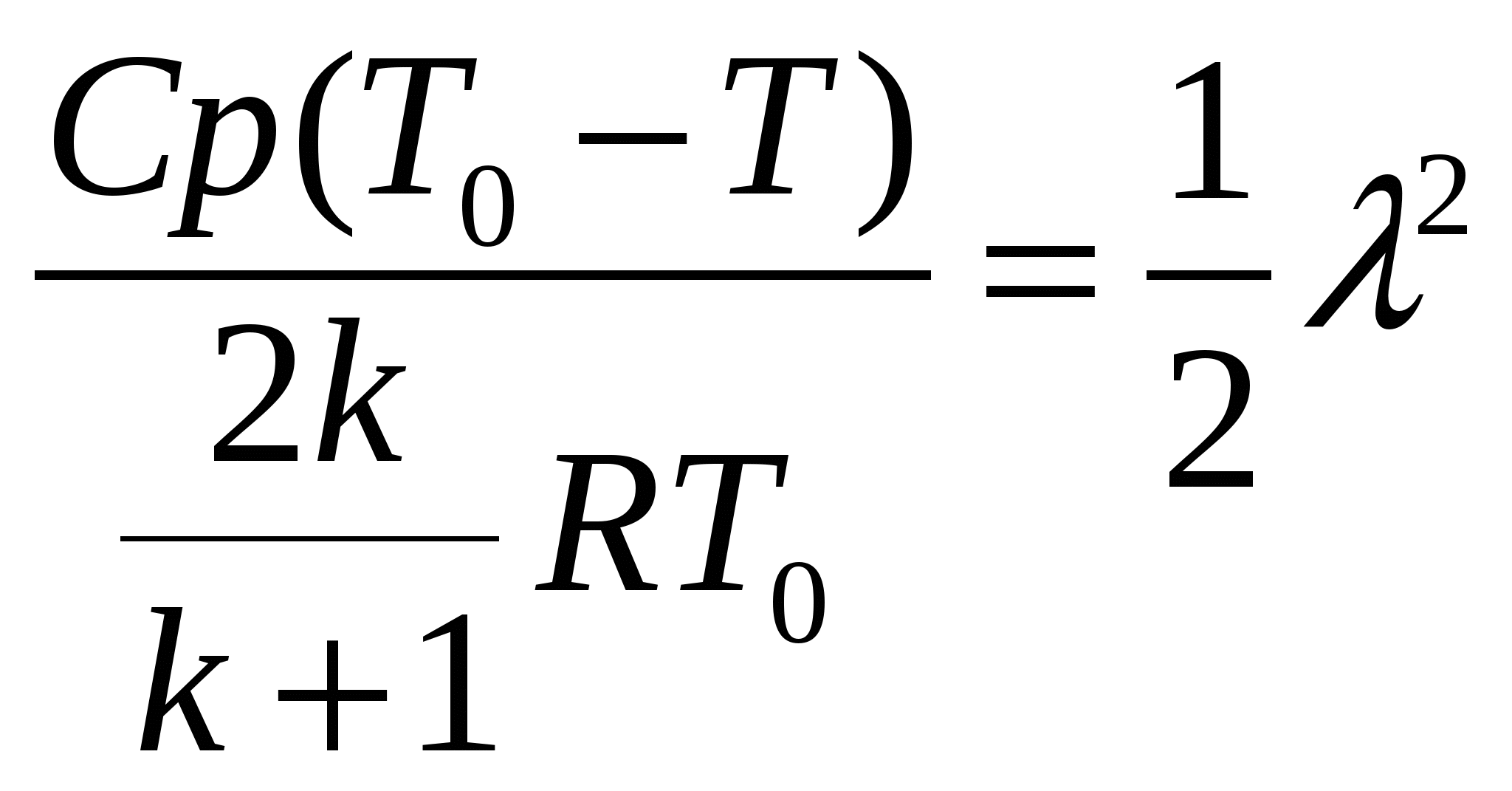 . .Отсюда принимая во внимание, что или Пользуясь соотношениями для идеальной адиабаты и зависимостью (6) можно получить формулу для давления и плотности: Связь между числами и М легко установить, сравнивая выражения (2) и (6): 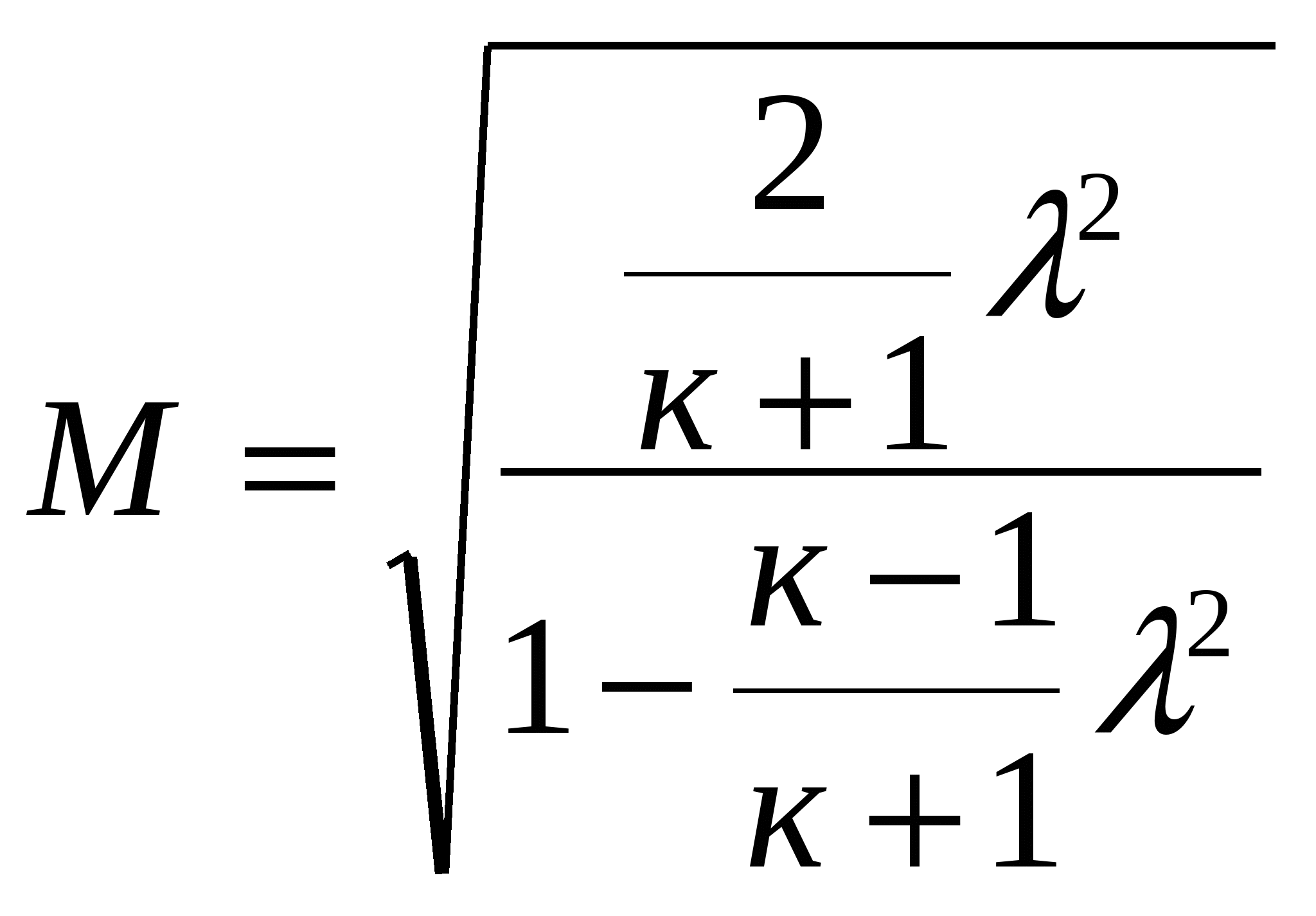 (9). (9).Зная значение числа или числа М и параметры торможения P0, T0, 0 c помощью приведённых соотношений легко найти параметры P, T, , характеризующие состояние движущегося газа. Реактивная сила, создаваемая струёй, истекающей из сопла Лаваля, может быть определена по формуле С изменением степени расширения сопла Если при Ркр > РС окажется РВ=РС, то говорят, что сопло работает в расчётных условиях, а истекающую струю считают расчётной. При РВ>РС истекающая струя будет недорасширенной, а при РВ < РС перерасширенной. На практике обычно обеспечивают степень расширения сопла Лаваля такой, чтобы сопло работало в расчётном режиме. Приведём зависимости для определения конструктивных параметров сопла, обеспечивающего получение заданной реактивной силы при минимальных затратах газа. При Рс=РВ из формулы (16) имеем: Поскольку Рс=РВ, то расчётное значение В можно найти с помощью газодинамической функции (): Добавляя к уравнениям (17) и (18) зависимость получим замкнутую систему уравнений, позволяющую при известных значениях F, P0, Pc, k определить площади кр и В сопла Лаваля, работающего в расчётном режиме. |
