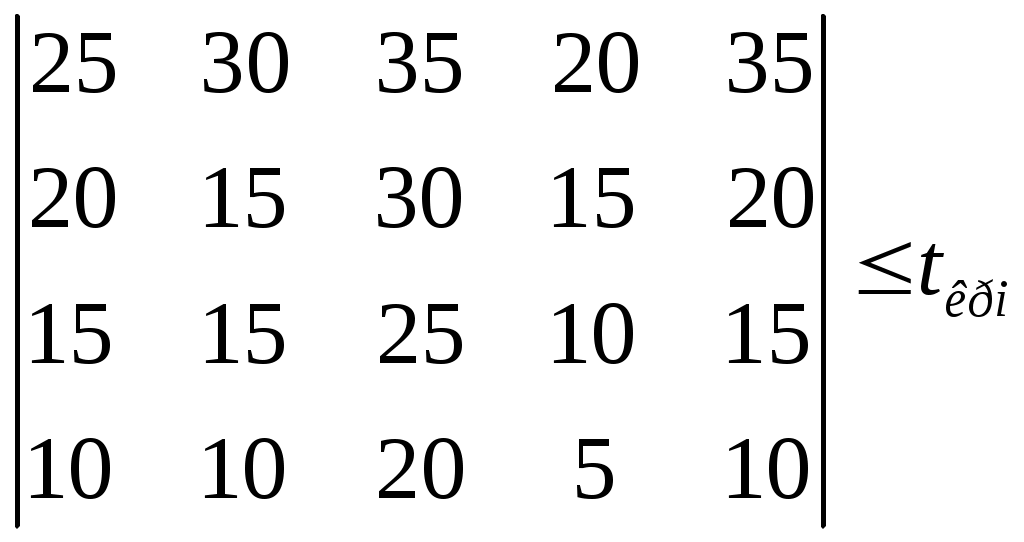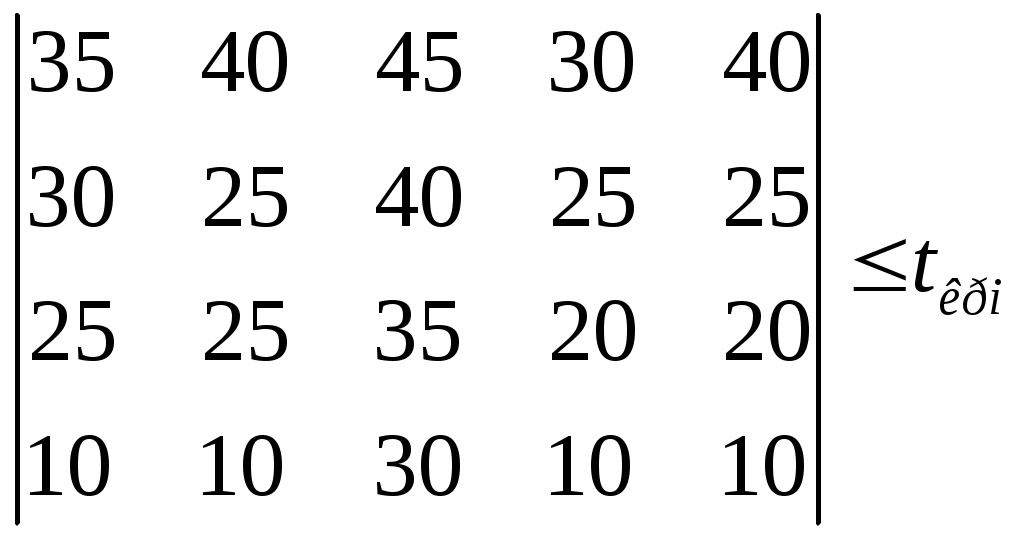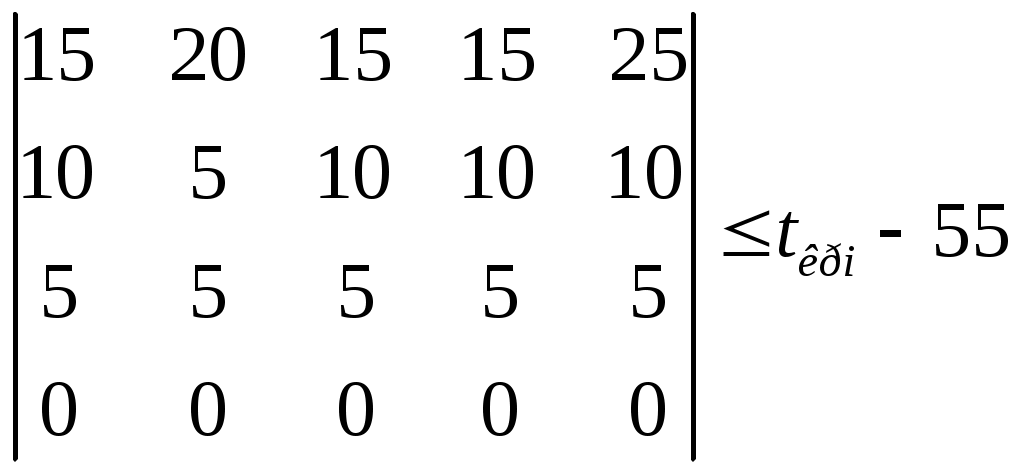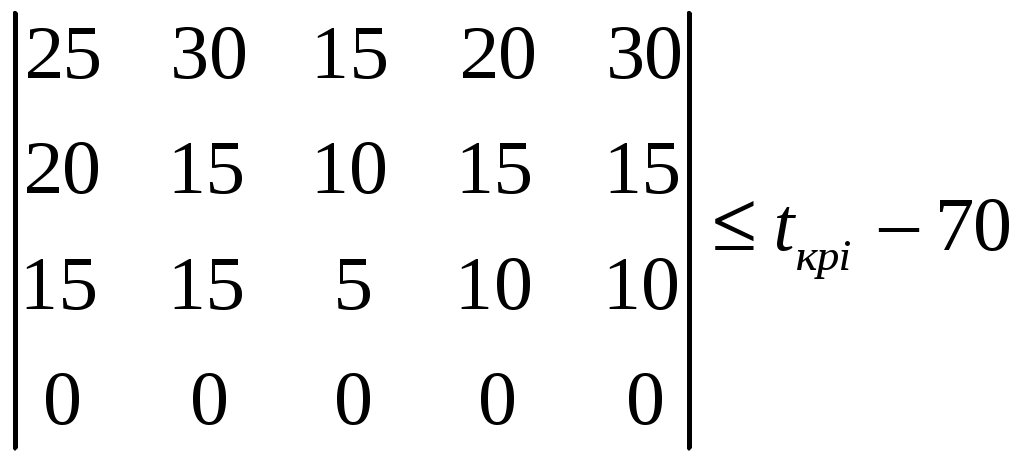Метод указ для контр работ. Методические указания для выполнения контрольной работы для студентовзаочников
 Скачать 175.5 Kb. Скачать 175.5 Kb.
|
|
Федеральное агентство по образованию Пензенская государственная технологическая академия Кафедра «Прикладная экономика» Юдаева Н.Ю. Логистика Методические указания для выполнения контрольной работы для студентов-заочников Пенза 2010 Методические указания предназначены и разработаны на кафедре «Прикладная экономика» ПГТА для студентов-заочников Контрольная работа №1 Формирование оптимальных логистических систем Контрольная работа заключается в разработке сложных логистических систем, интегрирующих необходимые этапы изменений материального потока. Решение задачи становится возможным при использовании экономико-математического моделирования. Цели контрольной работы: помочь студентам закрепить полученные в процессе обучения знания по применению основного принципа логистики – принципа интеграции; научить студентов применять полученные знания на практике; стимулировать самостоятельную творческую работу студентов при решении конкретных логистических задач; помочь студентам овладеть методами математического программирования для получения наиболее эффективных решений. Методические указания по выполнению контрольной работы Логистические системы. Оптимизация логистических систем. Логистическая система – это адаптивная система с обратной связью, выполняющая те или иные логистические функции. Она, как правило, состоит из нескольких подсистем и имеет развитые связи с внешней средой. В качестве элементов могут рассматриваться как отдельные предприятия (рис 1.,а), так и элементы предприятия (рис 1.,б). 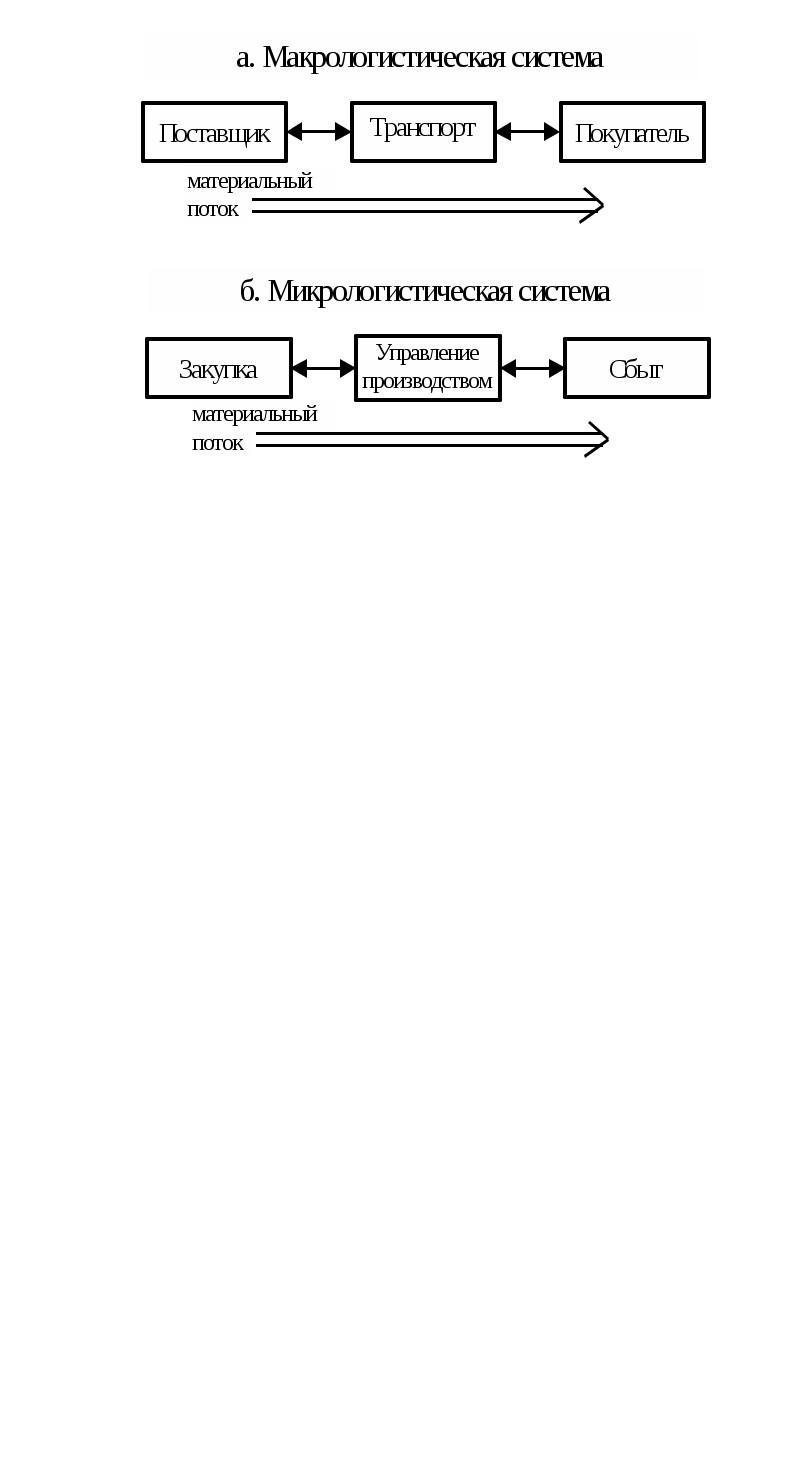 Рис.1. Принципиальная схема логистических систем. Одним из свойств логистической системы является наличие интегративных качеств, присущих системе в целом, но несвойственных ни одному из ее элементов в отдельности. Так, например, оптимальная эффективность системы, как правило, не совпадает с оптимальной эффективностью отдельных ее элементов. Если элементами логистической системы являются отдельные предприятия, очевидно возникновение противоречий между ними в процессе функционирования системы. Эти противоречия устраняются использованием компромиссов. Экономические компромиссы – категория, применяемая в процессе принятия решений по комплексу вопросов предпринимательской деятельности. Она выражается в расчетах, отражающих интересы, как различных подразделений фирм, так и всех фирм участниц логистической системы. Причём критерий эффективности системы всегда должен иметь приоритет перед эффективностью отдельных ее элементов. Компромисс здесь может быть достигнут за счет справедливого распределения прибыли системы, которая, как правило, должна быть больше потерь, возникающих у отдельных элементов, образующих эту логистическую систему. Наиболее действенным путем создания логистических систем, обеспечивающих эффективное управление сквозными материальными потоками, является переход к единому руководству. Задание. Выполнение контрольной работы предусматривает: А. Разработку оптимальной логистической системы. Для этого необходимо использовать экономико-математическое моделирование, оптимизационные методы решения этих задач. Б. Организацию рационального управления материальным потоком в элементах системы – процессе производства и материальных запасах. Исходные данные по вариантам выполнения контрольной работы представлены: для задачи А в таблицах 1, 2. для задачи Б в таблицах 1, 4. А. Разработка оптимальных логистических систем. Постановка задачи. В связи с тем, что свойства логистических систем на макро- и микро- уровнях совпадают, обоснованным является использование общих методов их формирования и оптимизации. Рассмотри два типичных примера из производственно-хозяйственной деятельности, требующих постановки и решения подобных задач. I. Формулировка задачи, требующей создания макрологистических систем. Производственная фирма в процессе расширения приобрела ряд организаций, обеспечивающих ранее доставку материалов и их складирование, складирование готовой продукции и её транспортировку на основную торговую базу, работу по сортировке груза и распределению в сеть магазинов. Единое управление всеми элементами логистической цепи создало условия для сквозного материального потока. Как известно, он определяется возможностью планировать параметры на выходе материального потока (т. А рис.2).  Рисунок 2. Управление сквозным материальным потоком. Для этого, по распоряжению руководства фирмы, работниками вновь вошедших в ее состав предприятий совместно с отделом логистики были разработаны альтернативные варианты модернизации всех элементов деятельности этих предприятий для достижения уже общей для всех цели – получения максимальной прибыли от производства и реализации продукции фирмы. Каждый вариант в итоге определялся стоимостными затратами, связанными с временем выполнения логистических функций, необходимых для эффективной деятельности фирмы. Появилась необходимость в выборе таких вариантов, которые обеспечили бы минимальные затраты для всего материального потока. II. Формулировка задачи, требующей создания микрологистической системы. Производственная фирма получила предложения от потребителя на новый вид продукции. Причем ей ставятся условия, чтобы продукция была изготовлена в необходимом количестве в заданный срок. Была названа и сумма, которую готов затратить потребитель за выполнени заказа. Анализируя возможности выполнения заказа, каждый отдел фирмы, являющийся частью логистической системы, (рис. 1б), разработал различные альтернативные варианты выполнения заказа: по закупке материалов и комплектующих, их складированию; по складированию готовой продукции. Каждый из этих вариантов имеет определенные стоимостные и временные затраты. Необходимо выбрать наиболее эффективные варианты, которые определили бы максимальную эффективность выполнения заказа для всей логистической системы (исходные данные в таблице). Для решения подобных задач целесообразна разработка экономико-математической модели и алгоритма ее решения. Решение задачи в общем виде. Экономико - математическая модель и алгоритм решения. Формализация задачи. Имеется m i-x логистических функций (закупка материала, его складирование, обработка, складирование готовой продукции и др.) каждая из них может быть выполнена различными j-ми способами (j=1,2,3,..,n) за определенное время tij. Каждому способу выполнения соответствуют определенные стоимостные затраты (Сij). Необходимо выбрать такой способ выполнения каждой логистической функции, который, образуя систему, позволил бы выполнить все функции, определяющие заказ, за необходимое время по заданному критерию эффективности. Критерий эффективности. За критерий эффективности принимаем максимальную прибыль: П=Ц-С , где Ц – цена заказа (по согласованию с потребителем); С – суммарная стоимость выполнения заказа. В связи с тем, что Ц определена, максимальная прибыль может быть получена при минимальном значении С. Экономико – математическая модель задачи. Под экономико – математической моделью понимается математическое описание исследуемого процесса или объекта. Для рассматриваемой задачи такая модель представляется следующим образом: 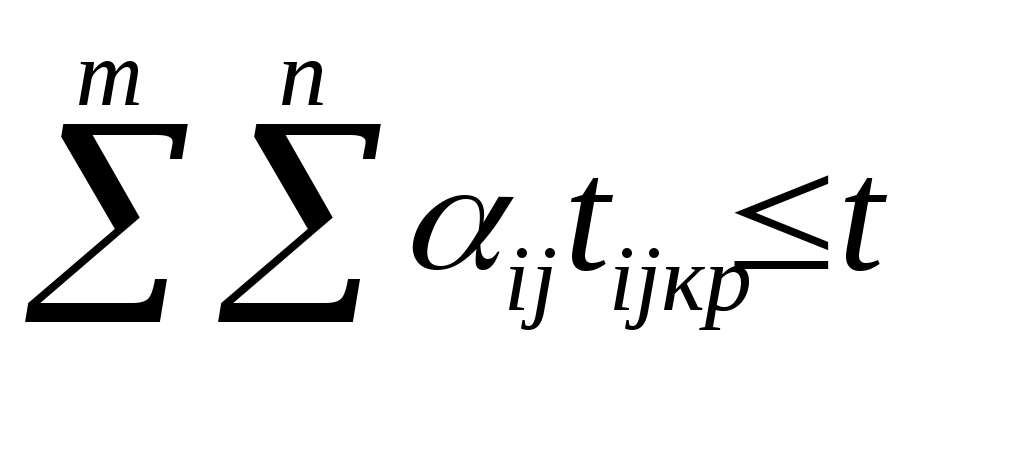 (0) (0)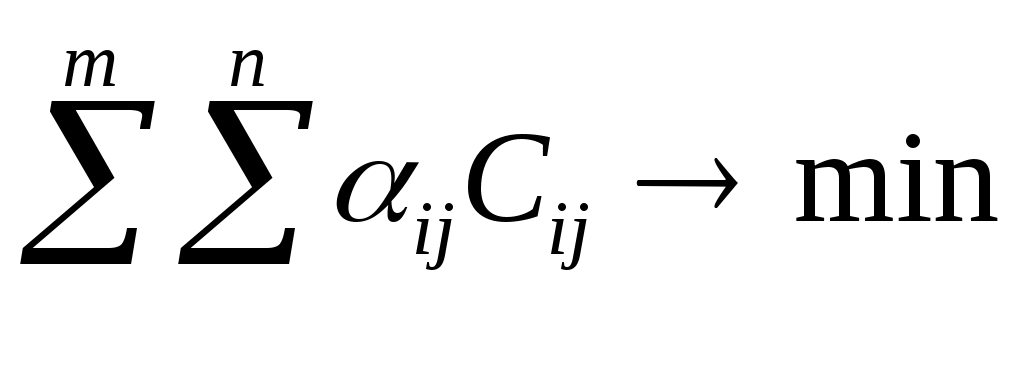 (0), (0),где tij – время выполнения i-й логистической функции j–м способом; Cij – стоимостные затраты при выполнении i-й – функции j- м способом; ij – параметр управления уравнением; αij=1 - если вариант оптимален, 0 - в противном случае. Эту задачу можно записать и иначе. Исходные значения времени выполнения i – х логистических функций, выполняемых j- ми способами представим в виде матрицы: 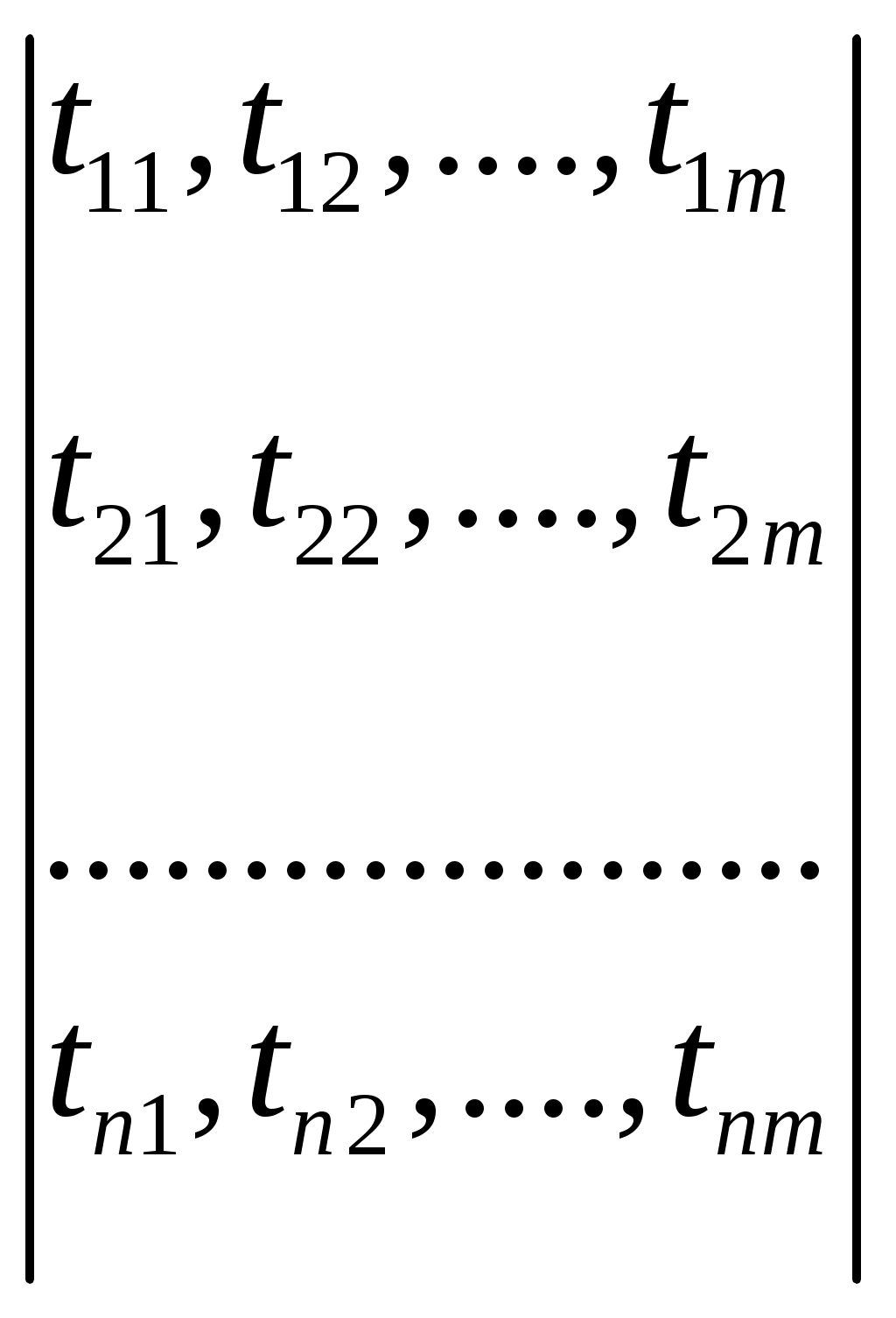 (0) (0)а значения стоимостных затрат – матрицей: 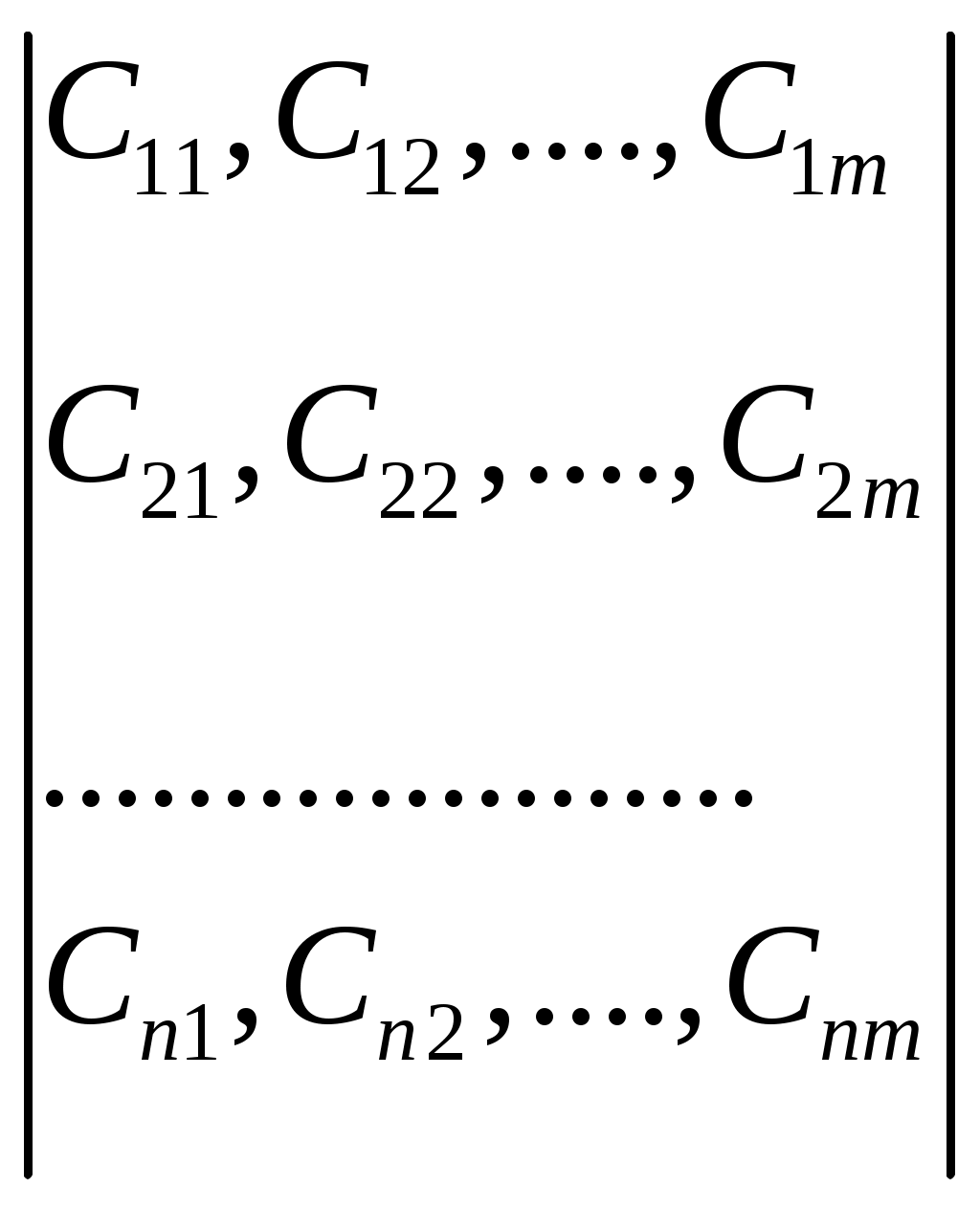 (0) (0)где n – количество альтернативных способов выполнения логистических функций; m – количество логистических функций выполняемых системой. Требования, выраженные условиями (1) и (2), сводятся к тому, чтобы для каждой i-й функции выбрать один вариант выполнения, т.е. в каждом столбце матрицы (3) и (4) оставить по одному значению tij и Cij, соответствующим затратам оптимальных вариантов для всей логистической системы. Алгоритм решения задачи Алгоритм решения задачи – точное предписание последовательности действий. Ряд задач, связанных с оптимизацией логистических систем, целесообразно решать методом динамического программирования. Под динамическим программированием понимается вычислительный метод, опирающийся на аппарат рекуррентных (возвратных) уравнений, разработанных Р. Беллманом. Этот метод применяется при решении задач упорядочения перебора вариантов. Метод динамического программирования применяется в том случае, если задачу можно представить как многошаговую. На каждом шаге выявляют вариант, при котором выбранная последовательность вариантов наилучшая по критерию эффективности. Пошаговое представление процесса позволяет свести решение многомерных задач к решению одномерных многошаговых. Для поставленной задачи алгоритм сводится к следующему. Исходные значения времени выполнения логистических функций tij и стоимостных затрат Cij записываются в виде матриц (3) и (4). Производится преобразование матриц, обеспечивающие следующее соотношение величин tij и Cijпо столбцам: 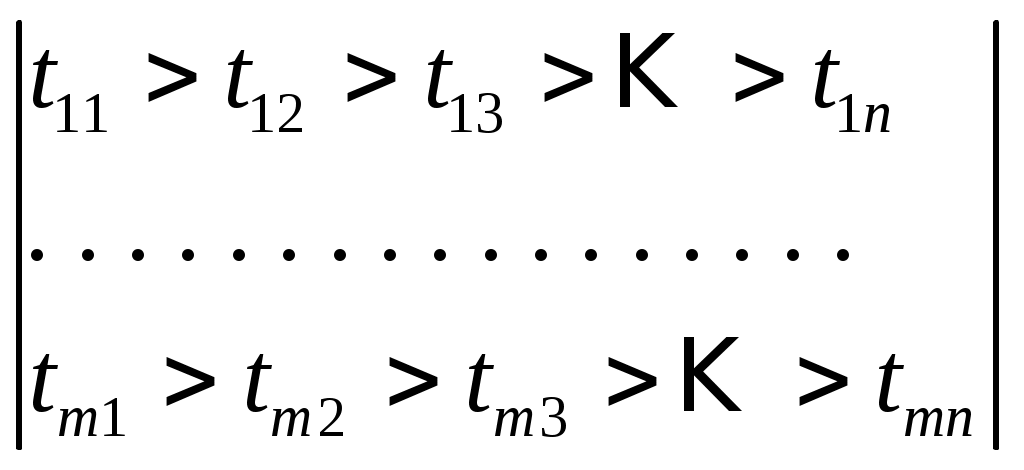 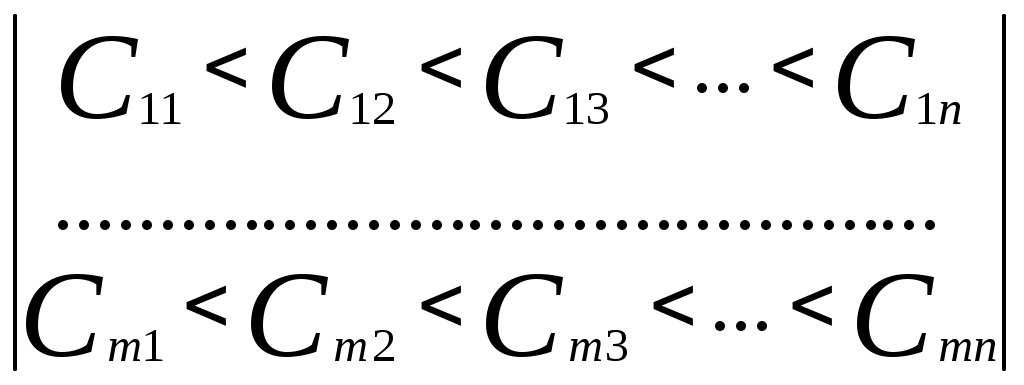 При больших значениях n и m (количестве альтернативных вариантов выполнения логистических функций и количестве элементов логистической системы), задача формирования оптимальной логистической системы решается как многомерная. Использование динамического программирования, а именно функциональных уравнений Р. Беллмана, позволяет свести решение многомерных задач к решению многошаговых одномерных. Для шага 1 [первый столбец матриц (3) и (4)], имеем: где f1(tкр)– зависимость стоимостных затрат при выполнении первой логистической функции от времени ее выполнения, т.е. первый столбец исходной матрицы Cij (4). Задаваясь значениями tij от tкр до 0 , осуществим выбор наиболее эффективного способа выполнения первой логистической функции, допустив что вся логистическая система состоит только из нее. Для шага 2 (с учетом обоих столбцов матрицы): При выборе оптимального варианта для m – функции, (шага - m) Примечание. Для удобства проведения расчетов без применения вычислительной техники, исходные данные в приведенных ниже задачах позволяют в алгоритме задаваться значениями Исходные данные временных затрат на выполнение логистических функций по вариантам (в раб. дн) Таблица 1.
Исходные данные стоимостных затрат при выполнении логистических функций по вариантам (тыс. руб.) Таблица 2.
Исходные данные с учетом поставленной задачи можно представить в виде матриц:
для вариантов контрольной работы с 1 по 25: С 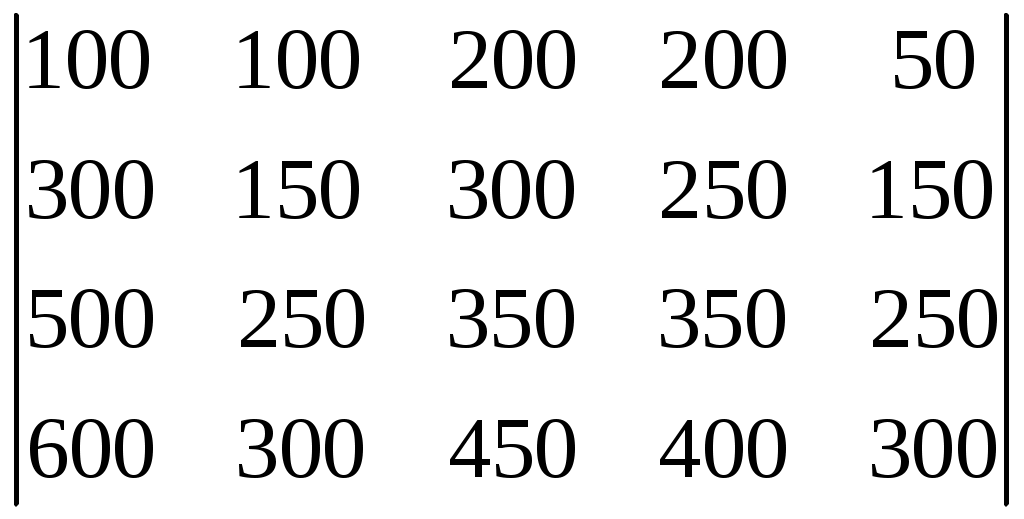 Преобразуем матрицы, вычтя из каждого столбца его минимальное значение. На эту же величину уменьшим и значение tкр. Получим :
C 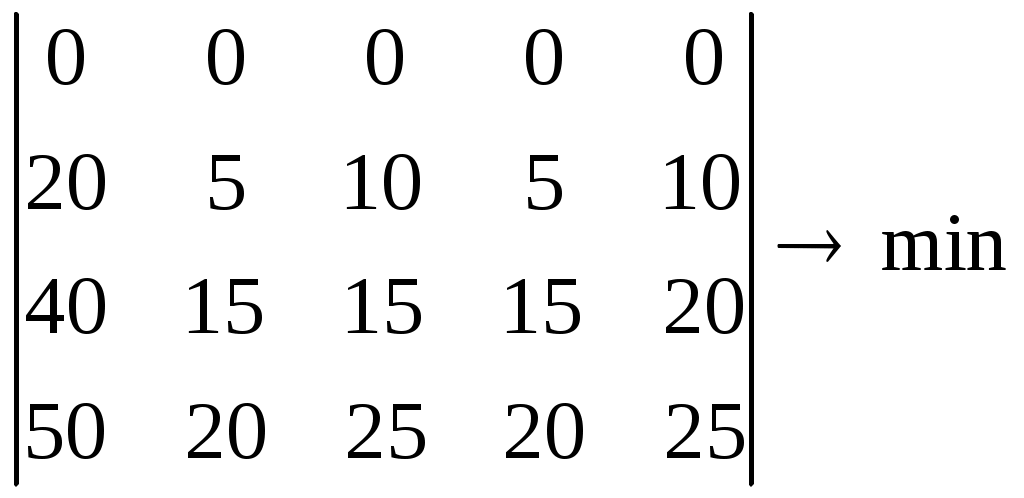 . .Далее производим решение в соответствии с приведенным выше алгоритмом. Примечание. Индивидуальность вариантов определяется различием критического времени (tкр), соответствующего выпуску определённой программы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||