электротехника. практикии. Методические указания и контрольные задания для студентов заочного отделения профессиональных образовательных учреждений специальностей

• Название: Методические указания и контрольные задания для студентов заочного отделения профессиональных образовательных учреждений специальностей
• Анкор: электротехника
• Дата: 22.06.2022
• Размер: 1.16 Mb.
• Имя файла: практикии.doc
• Тип: Методические указания; #611101
• страница: 9 из 11

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
Указания к решению задачи № 1

Рассмотрим решение типовой задачи. Задача относится к теме «Электрическая цепь постоянного тока». После усвоения условия задачи проводим поэтапное решение.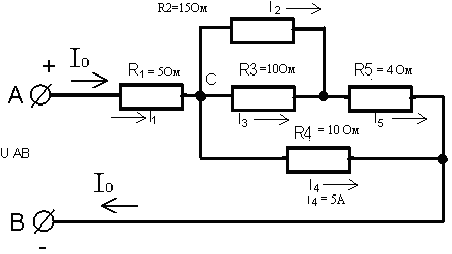



Рисунок А.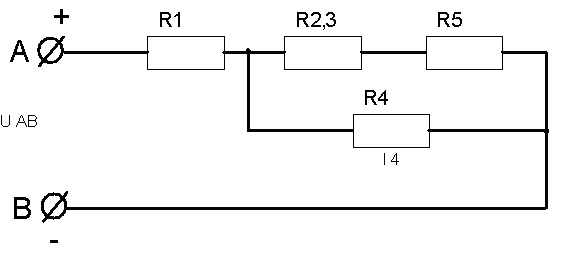



Рисунок Б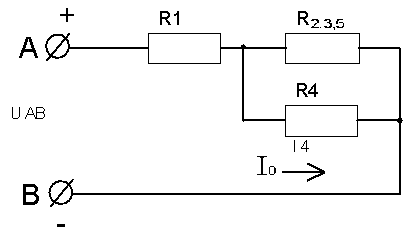




Рисунок В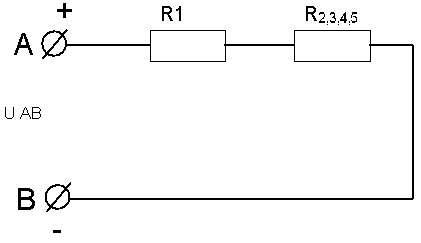



Рисунок Г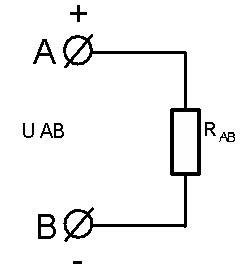



Рисунок Д
Пример №1.

Для схемы, приведенной на рисунке А, определить эквивалентное сопротивление цепи R_АВ, токи в каждом резисторе, падения напряжения на участках цепи U_1-5 и напряжение U_АВ, приложенное к цепи, а также мощности, потребляемые участками цепи Р_1-5 и всей цепью Р_общ. Заданы сопротивления резисторов R_1-5 и ток I₄ в резисторе R₄ (на рисунке А).
Указание:прежде всего, выполните «анализ» электрической схемы, представленной на рисунке А (с «конца» в «начало» (к источнику питания)), с целью выявления явно выраженных групп с параллельным и последовательным соединением резисторов. После чего, применяя законы для определения электрических параметров для выявленных групп соединений, определите эти параметры и начертите преобразованную (с эквивалентными сопротивлениями) электрическую схему, и уже на ее базе вновь повторите предыдущие действия и т.д., вплоть до определения эквивалентного (общего) сопротивления R_АВ .
Решение.

1. 
   Определяем общее сопротивление разветвления R₂, R₃. Эти резисторы соединены параллельно, поэтому:
   

Ом

Схема цепи принимает вид, приведенный на рисунке Б.

2. 
   Резисторы R₂,₃ и R₅ соединены последовательно, поэтому их общее сопротивление равно:
   

Ом

Схема принимает вид, приведенный на рис.В

3. 
   Группа резисторов R_2,3,5 и R₄ соединены параллельно, поэтому их общее сопротивление равно:
   

Ом

Схема цепи имеет вид, приведенный на рис.Г

4. 
   Находим эквивалентное (общее) сопротивление R_АВ всей цепи. Исходя из того, что R_2,3,4,5 соединено последовательно с R_{5, то} R_АВ определяем по формуле:
   

= 5 + 5 = 10 Ом

5. 
   Зная силу тока I_4, используя закон Ома для участка цепи, находим падение напряжения U₄ на резисторе R₄:
   

В

6. Это же напряжение U₄ приложено к группе последовательно соединенных резисторов R_2,3+ R₅ (рис.Б). Так как группа резисторов R₂,_3,5 включена параллельно к резистору R₄, то U_2,3,5 = U_4, поэтому ток I₅ в резисторе R₅ находим по формуле:

А

7. Используя закон Ома для участка цепи, находим падение напряжения U₅ на резисторе R₅ :

В

8. Поэтому напряжение на резисторах R_2,3 (т.к. они включены параллельно),
В

7. 
   Определяем токи в резисторах R₂ и R₃ по закону Ома:
   

А

А

8. Применяя первый закон Кирхгофа для узла С, находим ток в резисторе R:

А,

по схеме видно что
9. Вычисляем падение напряжения на резисторе R₁:

В

10. Находим напряжение U_АВ, приложенное ко всей цепи

В или

В

11. Определяем величины мощностей Р_1-5 потребляемые резисторами Р_общ., а именно:










Указания к решению задач № 2 и № 3
Решение этих задач требует знания физических процессов, возникающих в цепях однофазного переменного тока с последовательным (неразветвленная цепь) соединением активного, индуктивного и емкостного сопротивлений и формул для расчета таких цепей.

Перед решением этих задач изучите материал темы 1.5, ознакомьтесь с методикой построения векторных диаграмм.

Пример №2.

Дана неразветвленная электрическая цепь переменного тока с активным сопротивлением R₁ = 6 Ом, индуктивным X_L = 10 Ом, активным сопротивлением R₂ = 2 Ом и емкостным сопротивлением X_С = 10 Ом (рисунок 37а). К цепи приложено напряжение Uаб = 50В.

Определить: 1) полное сопротивление цепи; 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощность; 5) падение напряжения на каждом сопротивлении. Начертить в масштабе векторную диаграмму тока и напряжений данной цепи.


Рисунок 37а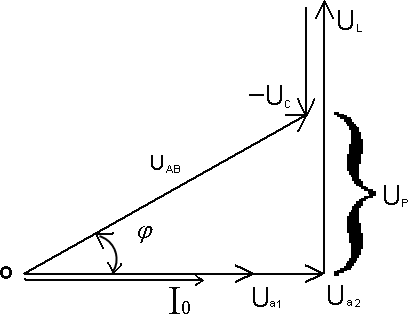



Рисунок 37 б

Решение:

1. 
   Определяем полное сопротивление цепи:
   

Ом.

2. 
   По закону Ома определяем общий ток в цепи:
   

А

3. 
   Определяем угол сдвига фаз φ из формул:
   

либо
по таблицам Брадиса находим φ = 36⁰50’. Угол сдвига фаз φ находим по синусу во избежание потери знака угла (косинус является четной функцией).

4. 
   Определяем активную мощность цепи по формулам:
   

Вт. или
Вт.

5. 
   Определяем реактивную мощность цепи:
   

Вар или
Вар

6. 
   Определяем полную мощность цепи:
   

ВА. или
ВА.
Определяем падение напряжения на сопротивлениях R1, X_L, X_С, R2 цепи используя закон Ома для участка цепи (т.к. цепь неразветвленная, общий ток цепи I_общ.. равен токам на участках):

U_a1 = I * R₁ = 5*6 = 60 B
В
U_a2 = I * R₂ = 5*2 = 10 B


Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см-1,0А и масштабом по напряжению: в 1 см – 10 В

Построение векторной диаграммы (рис.37,б) начинаем с вектора тока, который откладываем по горизонтали в масштабе Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях : . Из конца вектора откладываем в сторону опережения вектора тока на 90⁰ вектор падения напряжения на индуктивном сопротивлении длиной . Из конца вектора откладываем в сторону отставания от вектора тока на 90⁰ вектор падения напряжения на конденсаторе длиной . Геометрическая сумма векторов равна полному напряжению U, приложенному к цепи. Угол между током и общим напряжением равен φ.
Пример №3.

Катушка с активным сопротивлением R₁=6 Ом и индуктивным X_L=8 Ом соединена параллельно с конденсатором, емкостное сопротивление которого X_С2=10 Ом (рисунок 38 а). К цепи приложено напряжение U_АВ = 100В.

Определить:

1) токи в ветвях и в неразветвленной цепи;

2) активные и реактивные мощности ветвей и всей цепи;

3) полную мощность цепи;

4) углы сдвига фаз между током и напряжением в каждой ветви и по всей цепи.

Начертить в масштабе векторную диаграмму токов цепи.

Решение.

Дана схема разветвленной электрической цепи переменного тока (рис. 38 a).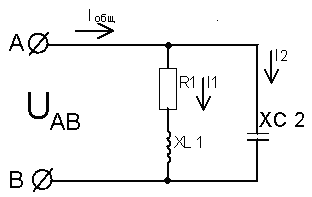



Рисунок 38а

1.Находим полное сопротивление первой ветви по формуле:
= Ом
2. Применяя закон Ома для участка цепи переменного тока, определяем ток в первой ветви:

А

3. Так как сопротивление второй ветви равно X_с2=10 Ом, то ток в ней равен:

А

4. Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла:

, тогда как , т.е. угол φ=53˚10΄. Так как φ₁›0, то напряжение опережает ток.

, то φ₂=-90˚., т.е. напряжение отстает от тока, так как φ₂<0.

По таблицам Брадиса находим , что cosφ₁=53˚10΄=0,6; cosφ₂=0
5. Определяем активные и реактивные составляющие токов в ветвях:

А;
А;
; А.
6. Определяем ток в неразветвленной части цепи по формуле:
А.
7. Определяем коэффициент мощности всей цепи по формуле:

2. 
   Определяем активные и реактивные мощности ветвей и всей цепи:
   

Вт
Вт
Вар
Вар
Вар

Внимание! Реактивная мощность ветви с емкостью отрицательная, так как φ₂<0.

3. 
   Определяем полную мощность цепи:
   

ВА.
Замечание: ток в неразветвленной части (общий) цепи можно определить значительно проще, без разложения токов на составляющие, зная полную мощность цепи и напряжение:

А

4. 
   Для построения векторной диаграммы задаемся масштабом по току: в 1 см – 2,5 А и масштабом по напряжению: в 1 см – 25В. Построение начинаем с вектора напряжения U (рис. 38.б). Под углом φ₁ к нему (в сторону отставания) откладываем в масштабе вектор тока I₁ под углом φ₂ (в сторону опережения) откладываем вектор тока I₂. Геометрическая сумма этих токов равна току в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая I_а1) и вектор, перпендикулярный ему (реактивные составляющие I_р1 и I_р2).
   

При отсутствии конденсатора реактивная мощность первой ветви не компенсировалась бы и ток в цепи увеличился бы до I= I₁ 10А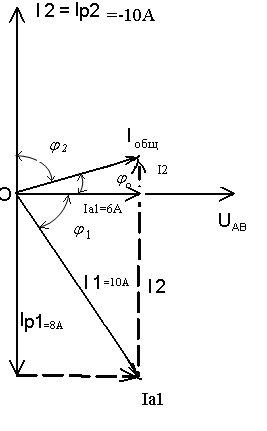



Рисунок 38 б

Указания к решению задач № 4 и № 5
Решение задач этой группы требует знания учебного материала темы «Трехфазные электрические цепи», следует иметь четкое представление об особенностях соединения источников и потребителей в звезду и треугольник, соотношения между линейными и фазными величинами при таких соединениях, а также уметь строить векторные диаграммы при симметричной и несимметричной нагрузках. Для пояснения общей методики решения задач, включая построение векторных диаграмм, рассмотрены типовые примеры 4 и 5.
Пример № 4.

В трехфазную четырехпроводную сеть включены звездой лампы накаливания мощностью P₁=300 Вт каждая. В фазу «А» включили 30 ламп,
в фазу «В» – 50 ламп и в фазу «С» – 20 ламп. Линейное напряжение сети