Алгоритмические языки_ Лабораторная работа №3 -... Методические указания к лабораторной работе 3 по дисциплине Алгоритмические языки и программирование для студентов специальности 230100 (ивт)
 Скачать 329 Kb. Скачать 329 Kb.
|
5. Теоретический материалИнициализация массива случайными числамиДля выполнения лабораторной работы №3 придется пользоваться массивами большого размера. Размеры массивов в данной работе могут достигать 15 тысяч элементов, что не позволяет реализовать ввод данных с клавиатуры. Для решения этой задачи предлагается использовать инициализацию массива случайными числами. Для работы с генератором случайных чисел необходимо создать объект стандартного класса Random: Random Rnd = new Random(); Инициализация массива выполняется с помощью метода Next класса Random и может выглядеть следующим образом: int maxValue = 100; int[] a = new int[1000]; for (int i = 0; i < 1000; i++) a[i] = Rnd.Next(0, maxValue); // Случайное число от 0 до 100 Измерение времени работы программыВ задании на лабораторную работу требуется измерить время работы программы. Для этого удобно воспользоваться стандартным классом Environment, который содержит свойство TickCount, в котором содержится время (в миллисекундах), прошедшее с момента загрузки операционной системы. Чтобы определить время работы какого-либо фрагмента кода, необходимо выполнить два замера времени (до и после этого фрагмента), а потом вычислить разность полученных значений. Для перевода результата в секунды можно разделить его на 1000. Вот как может выглядеть текст функции Main(), в котором производится замер времени работы фрагмента кода: static void Main(string[] args) { // Здесь выполняется инициализация данных (ввод массивов и проч.) int t1 = Environment.TickCount; // Здесь выполняется основная работа программы ...... int t2 = Environment.TickCount; // Печать затраченного времени на экране Console.WriteLine("Продолжительность работы: " + (t2 - t1) / 1000.0); // Печать полученного массива } Сортировка пузырькомИдея метода: шаг сортировки состоит в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами. 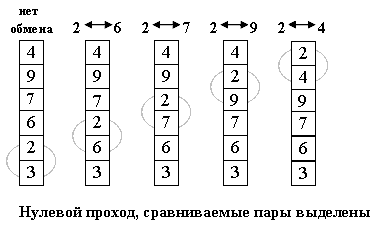 После нулевого прохода по массиву "вверху" оказывается самый "легкий" элемент - отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом, второй по величине элемент поднимается на правильную позицию... Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию. 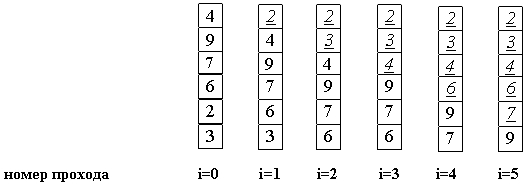 Алгоритм сортировки «пузырьком» представлен ниже: i-цикл от 0 до size с шагом 1 j-цикл от size-1 до i с шагом -1 если a[j-1] > a[j], то x = a[j-1] a[j-1] = a[j] a[j] = x все если все j-цикл все i-цикл Среднее число сравнений и обменов имеют квадратичный порядок роста: O(n2), отсюда можно заключить, что алгоритм пузырька очень медленен и малоэффективен. Сортировка выборомИдея метода состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке. Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м. На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рисунке ниже. 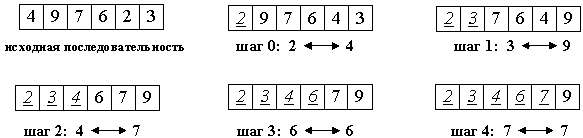 Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] (выделена курсивом) является упорядоченной. Таким образом, на (n-1)-м шаге вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево. Алгоритм сортировки выбором представлен ниже: i-цикл от 0 до size с шагом 1 k = i x = a[i] j-цикл от i + 1 до size с шагом 1 если a[j] < x, то k = j x = a[j] все если все j-цикл a[k] = a[i] a[i] = x все i-цикл Для нахождения наименьшего элемента из n+1 рассматриваемых алгоритм совершает n сравнений. С учетом того, что количество рассматриваемых на очередном шаге элементов уменьшается на единицу, общее количество операций: n + (n-1) + (n-2) + (n-3) + ... + 1 = 1/2 * ( n2+n ) = O(n2) Таким образом, так как число обменов всегда будет меньше числа сравнений, время сортировки растет квадратично относительно количества элементов. Алгоритм не использует дополнительной памяти: все операции происходят "на месте". |
