Методические указания к практическим занятиям и самостоятельной работе для студентов направлений
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
Занятие 5. Эквивалентные и эффективные ставкиОдин и тот же финансовый результат можно получить различными способами, используя различные ставки. Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не меняются. Эффективная процентная ставка позволяет сравнивать финансовые операции с различной частотой начисления и неодинаковыми процентными ставками. Именно эта ставка характеризует реальную эффективность операции, однако во многих финансовых контрактах речь чаще всего идет о номинальной ставке, которая в большинстве случаев отличается от эффективной. Меняя частоту начисления процентов или вид ставки, можно существенно влиять на эффективность операции. В частности, оговоренная в контракте ставка может при определенных условиях вовсе не отражать истинный относительный доход (относительные расходы). Например, 6% годовых при условии ежедневного начисления процентов соответствуют на самом деле 8,21%, начисляемых ежегодно. Отмеченная особенность исключительно значима в условиях высоких номинальных ставок. При составлении финансовых договоров данный прием нередко используется для сокрытия истинных расходов. Поэтому, заключая контракт, целесообразно уточнять, о какой ставке (процентной, учетной, эффективной и др.) идет речь или, по крайней мере, отдавать себе отчет в этом. Цель проведения занятия - научиться проводить расчеты по замене ставок и условий финансовых контрактов, используя формулы финансовых вычислений; сравнивать эффективность различных финансовых операций. Основные формулы re=(1 + r/m)m – 1 (5.1) re=e - 1 (5.2) 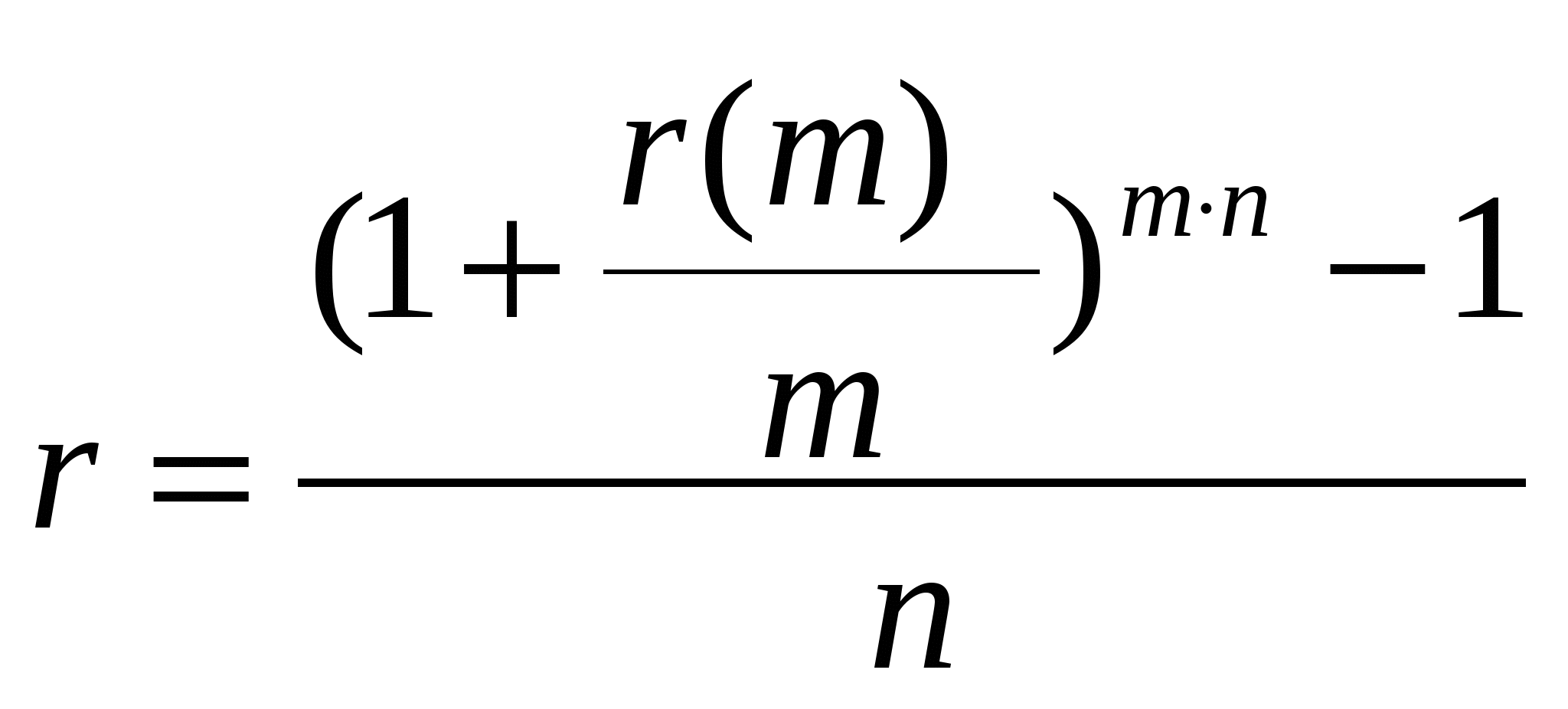 (5.11) (5.11)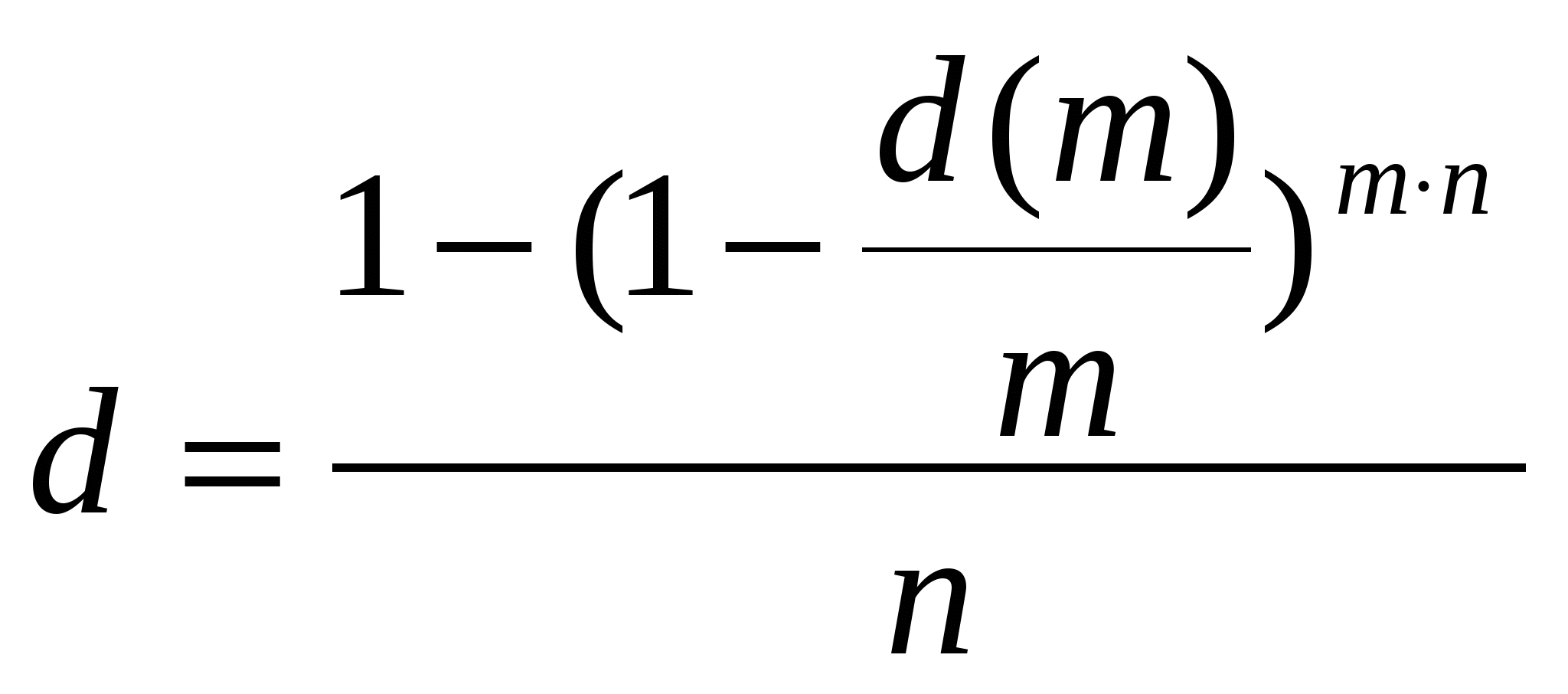 (5.12) (5.12)где r - простая процентная ставка, d - простая учетная ставка, rс - сложная ссудная ставка, dс – сложная учетная ставка, r(m ) -сложная процентная ставка с начислением процентов m раз за период, d(m) -сложная учетная ставка с начислением процентов m раз за период, n - продолжительность финансовой операции в годах Типовые задачи с решениями Задача 1. Какие условия предоставления кредита и почему более выгодны банку: 1) 28% годовых с ежеквартальным начислением процентов; 2) 30% годовых с полугодовым начислением процентов? РешениеРассчитаем эффективную годовую процентную ставку для каждого варианта. 1) По формуле (5.1) при r=0,28; m=4 re = (1 + 0.28/4)4 – 1 =0,3107= 31,1% 2) По формуле (5.1) при r=0,32; 2=4 re = (1 + 0.3/2)2 – 1 =0,3225= 32,25% Для банка выгоднее предоставлять кредит по варианту 2), так как в этом случае эффективная годовая ставка выше (предоставлять кредит под 32,25% годовых выгоднее, чем под 31,1%). Задача 2. Cрок уплаты по долговому обязательству – полгода, простая учетная ставка – 18% годовых . Какова доходность этой операции, измеренная в виде простой ставки ссудного процента? Решение По формуле (5.7) при d=0,18; n=0,5 r = 0,18 / (1-0,50,18) =0, 198. Доходность операции, выраженная в виде простой ставки ссудного процента, равна 19,8% годовых. Задача 3. Определить, под какую ставку ссудных процентов выгоднее поместить капитал в 10 млн. руб. на пять лет – под простую ставку 14% годовых или под сложную ставку 12% при ежеквартальном начислении процентов? Решение. В данном случае можно не считать наращенную сумму, поэтому не важна величина первоначального капитала. Достаточно, например, найти простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой эквивалентности по формуле (5.11) при r(m)=0,12; n=5; m=4: 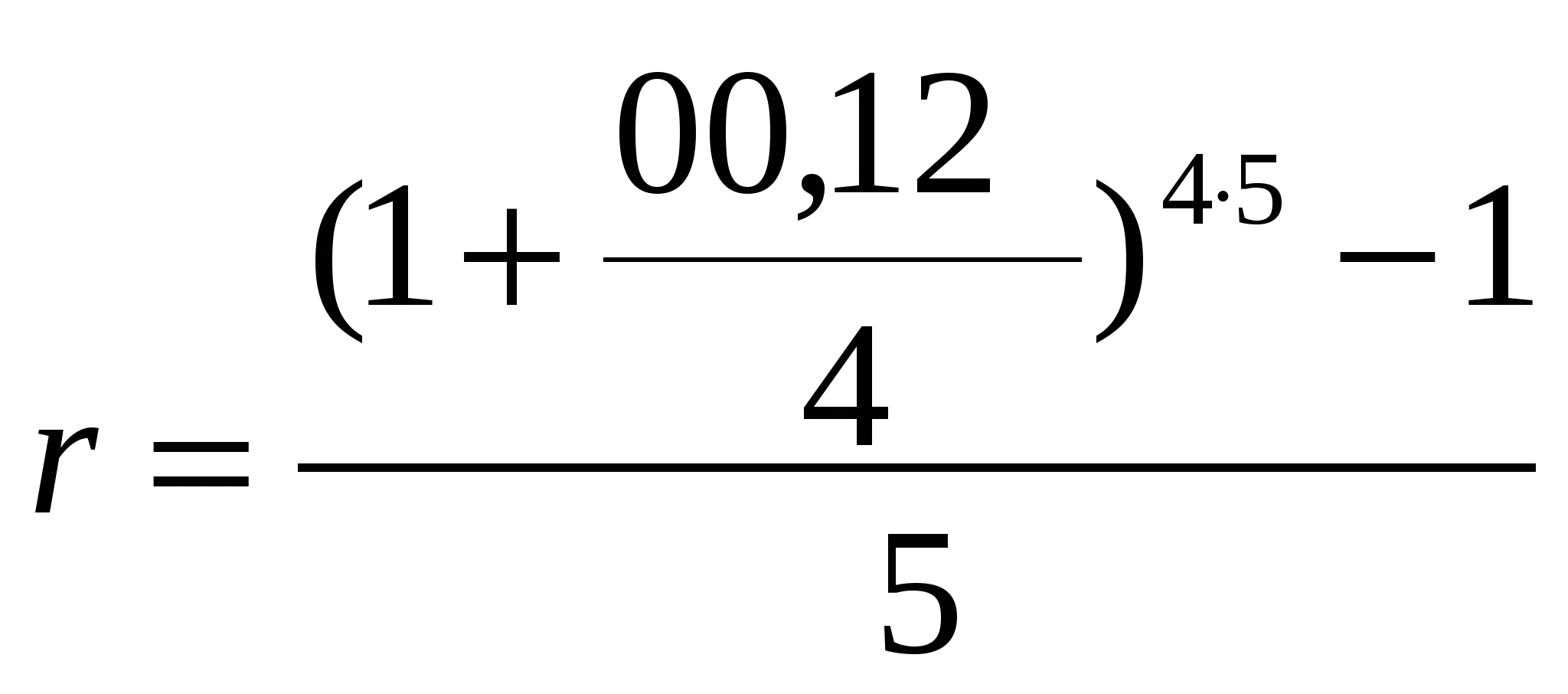 =0,1612 =0,1612Так как простая процентная ставка 16,12% , которая дала бы одинаковый результат с данной сложной процентной ставкой больше предложенной ставки в 14%, ясно, что предпочтительнее использовать сложную процентную ставку. Чтобы убедиться, насколько сложная ставка выгоднее, определим наращенные суммы: F (14%) = 17 F (16,12%) = 22,04 Владелец капитала в 10 млн. руб. за 5 лет может накопить 17 млн. руб. с использованием простой ставки 14% годовых; с использованием сложной ставки 12% годовых при ежеквартальном начислении процентов можно накопить 22,04 млн. руб. Задача 4. На капитал в сумме 500 тыс. руб. ежегодно начисляются сложный проценты по ставке 8% годовых в течение 5 лет. Определить эквивалентную ставку непрерывного начисления процентов (силу роста). Решение. По формуле (5.2) при r=0,08; m=1 Таким образом, ежегодное начисление процентов по ставке 8% эквивалентно непрерывному начислению процентов по ставке 7,7 %. Задача 5. Определить номинальную ставку, если эффективная ставка равна 9 % и сложные проценты начисляются ежемесячно. Решение. По формуле (5.4) при r(e) =0,09; m=12 r = 12 [(1 + 0,09)1/12 - 1 ] = 0,086 Таким образом, ежегодное начисление сложных процентов по ставке 9% годовых дает тот же результат, что и ежемесячное начисление сложных процентов по ставке 8,6 %. Задачи для подготовки к занятию Задача 1. Определить номинальную учетную ставку, если годовая эффективная учетная ставка равна 20% годовых и учет осуществляется 1) каждые полгода; 2) ежеквартально; 3) ежемесячно. Задача 2. Ссуда выдана при условии начисления сложных процентов по ставке 8 % годовых. Определить эквивалентную простую ставку при сроке ссуды 5 лет, 180 дней, 365 дней. Задача 3. Банком выдан кредит на 9 месяцев под 24% годовых с ежеквартальным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов. Задание на практическое занятие 5. Эффективные и эквивалентные ставки. Контрольные вопросы
Задача 1. Вексель учитывается за 180 дней до срока погашения по простой учетной ставке 10 % годовых. Какова доходность этой операции для банка, выраженная по сложной учетной ставке? Задача 2. Банк учитывает вексель за 300 дней до срока погашения по сложной учетной ставке 10% годовых при временной базе 360 дней. Какая простая годовая процентная ставка должна быть применена при выдаче кредита, если используется временная база 365 дней и банк хочет получить такой же доход? Задача 3. Банк выдает ссуду под сложную процентную ставку 20% годовых. Какую простую годовую процентную ставку должен установить банк, чтобы его доход не изменился, если начисление процентов происходит а) по полугодиям; б) каждые 2 месяца; в) каждую неделю. Задача 4. Определить номинальную годовую учетную ставку с дисконтированием 4 раза в год, эквивалентную номинальной годовой учетной ставке 12% с дисконтированием 12 раз в год. |
