Методические указания к практическим занятиям и самостоятельной работе для студентов направлений

• Название: Методические указания к практическим занятиям и самостоятельной работе для студентов направлений
• Дата: 24.04.2018
• Размер: 0.78 Mb.
• Имя файла: fm_230100_230200.doc
• Тип: Методические указания; #42025
• страница: 3 из 12

Занятие 3. Сложные ссудные ставки

Схема сложных процентов предполагает их капитализацию, т.е. база, с которой происходит начисление, посто­янно возрастает на величину начисленных ранее процентов. Более частое начисление сложных процентов обеспечи­вает более быстрый рост наращиваемой суммы.

Для кредитора более выгодна схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода). Для кредитора более выгодна схема сложных процентов, если срок суды превышает один год (проценты начисляются ежегодно). Обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

При начислении процентов за дробное число лет может использоваться схема сложных процентов, либо смешанная схема, предусматривающая начисление сложных процен­тов за целое число лет и простых процентов за дробную часть года.

Математическим дисконтированием (дисконтированием по сложной процентной ставке) называется задача нахождения такой величины первоначального капитала, которая через заданное количество времени при наращении по сложной процентной ставке обеспечит получение планируемой суммы.

Начисления сложных процентов могут быть дискретными и непрерывными. Уменьшая период начисления и увеличивая частоту начисления процентов переходят к так называемому непрерывному проценту, при котором наращенная сумма (при схеме сложных процентов) увеличивается максимально. Формулы для вычисления наращенной суммы при начислении ссудных и учетных процентов совпадают, т.к. при уменьшении периода начисления разница между начислением процентов в начале и в конце периода исчезает. Непрерывную ставку начисления процента обозначают  и называют силой роста.

Цель проведения занятия - научиться проводить расчеты по схеме сложных ссудных процентов, используя формулы финансовых вычислений; провести сравнение финансовых операций при использовании простых и сложных ставок.

Основные формулы
F=P∙ (1 + r) (3.1)

P = F /(1 + r)ⁿ (3.2)

F = P (1 + r/m)^nm(3.3)

F = P (1 + r)^w+f (3.4)

F=P(1+r)^w.(1+f∙r) (3.5)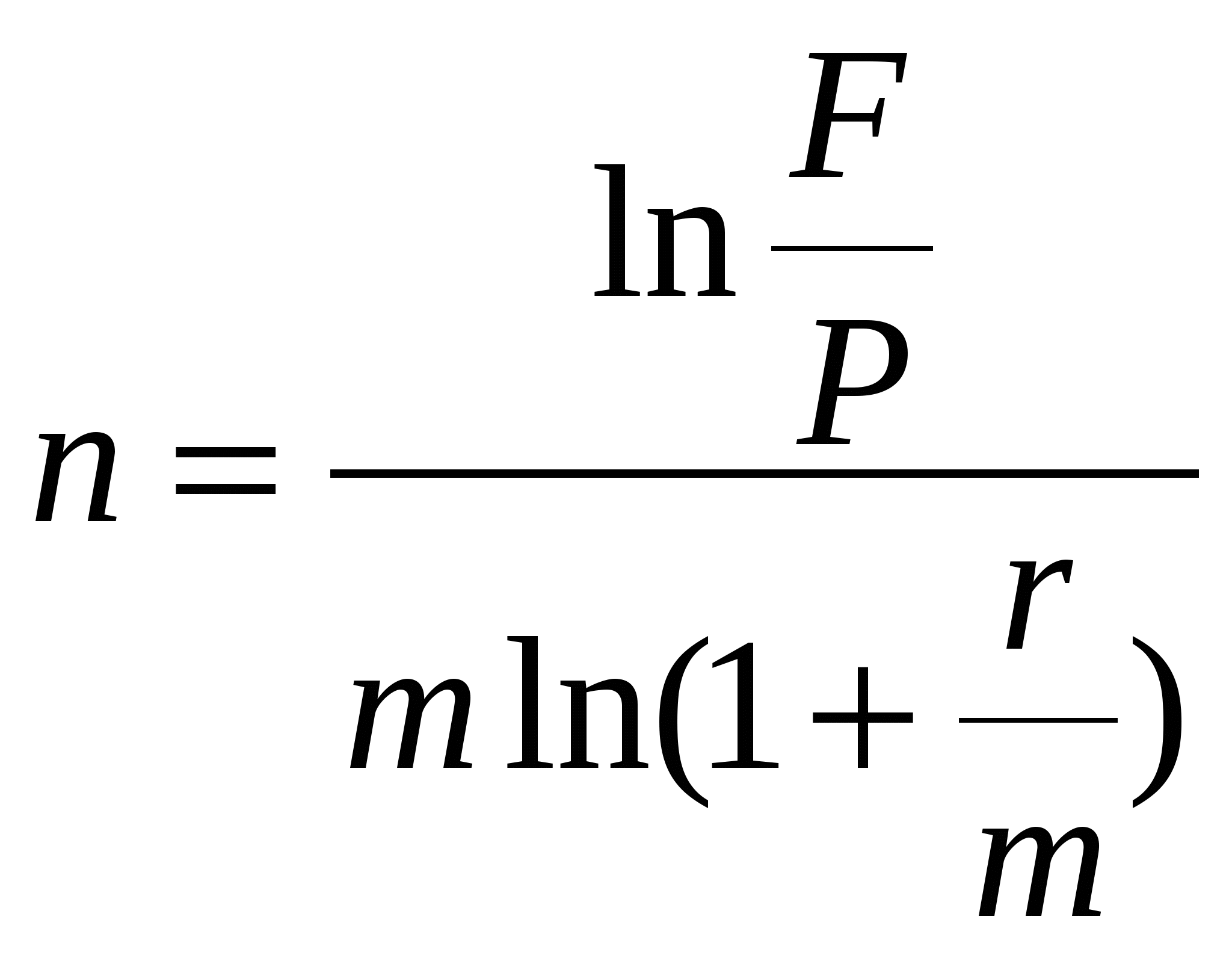
(3.6)

(3.7)

(3.8)

(3.9)

(3.10)
где

F– наращенная сумма;

P- вложенная сумма;

n- количество лет;

r- сложнаяпроцентная ставка;

m- количество начислений процентов в году;

w- целая часть периода финансовой операции;

f- дробная часть периода финансовой операции.
Типовые задачи с решениями

Задача 1. На вашем счёте в банке 15 млн. руб. Банковская ставка по депозитам равна 12% годовых. Вам предлагают войти всем капиталом в организацию совместного предприятия, обещая удвоение капитала через 5 лет. Принимать ли это предложение?

Решение.

Для решения задачи используем формулу (3.1.).

Если мы вложим деньги в банк, то через 5 лет получим следующую сумму:

F = 15∙(1 + 0,12)⁵ = 26,43 млн.руб.

Если мы войдем всем капиталом в организацию совместного предприятия, то наш капитал удвоится:

F = 15  2 = 30 млн. руб.

Следует принять данное предложение и не вкладывать деньги в банк.

Задача 2. Через 2 года ваш сын будет поступать в университет на коммерческой основе. Плата за весь срок обучения составит 5600 долл., если внести её в момент поступления в университет. Вы располагаете в данный момент суммой в 4000 долл. Под какую минимальную ссудную ставку нужно положить деньги, а банк, чтобы накопить требуемую сумму?

Решение.

Для решения задачи используем формулу (3.7) при m=1:

r = (5600 / 4000 )^1/2 – 1 = 0,1832 = 18, 32%

Для того чтобы накопить нужную сумму, минимальная ссудная сложная ставка должна составлять 18,32 % годовых.

Задача 3. За выполненную работу предприниматель должен получить 600 тыс. руб. Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок уплаты на 2 года, по истечении которых он обязуется выплатить 730 тыс. руб. Выгодно ли это предпринимателю, если приемлемая норма прибыли составляет 10%? Какова минимальная ставка, которая делает подобные условия невыгодными для предпринимателя?

Решение.

Для решения задачи используем формулу (3.1).

Будущая стоимость 600 тыс.руб. через 2 года при норме прибыли 10% составит:

F = 600 тыс.руб. (1 + 0,1)² = 720,6 тыс.руб.

Это меньше, чем 730 тыс. руб., поэтому предпринимателю выгодно ждать расчета 2 года.

Для расчета минимальной ставки, которая делает условия невыгодными, воспользуемся формулой (2.6) при m=1:

r = (730 /600)^1/2 – 1 = 0,1030 =10,3 %

Минимальная ставка, которая делает условия невыгодными для предпринимателя, равна 10,3 % годовых.

Задача 4. Банк предоставил ссуду в размере 5000 долл. на 39 месяцев под 10% годовых на условиях полугодового начисления процентов. Рассчитайте возвращаемую сумму при различных схемах процентов: 1) схема сложных процентов; 2) смешанная схема.

Решение

Для решения воспользуемся формулами для вычисления наращенной суммы, если продолжительность финансовой операции не равна целому числу лет.

1. 
   Схема сложных процентов - формула (3.4), считая полугодие базовым периодом;
   

w=6; f = 3,252-6=0,5; r=5%:

F =5000 (1+0,05)^6+0,5=6865, 9

По схеме сложных процентов возвращаемая сумма равна 6865, 9 долл.

2. 
   Смешанная схема – формула (3.5), считая полугодие базовым периодом;
   

w=6; f = 3,252-6=0,5; r=5%:

F = 5000 ·(1+0,05)^6.(1+0,50,05) = 6867,99

По смешанной схеме возвращаемая сумма равна 6867,99 долл.

Задача 5. 1 августа 2010 г. должник обязан уплатить кредитору 400 тыс. руб. Какую сумму необходимо иметь должнику, если он вернет деньги : 1) января 2010 г.; 2) 1 января 2011 г.; 3) 1 августа 2010 г.? Деньги взяты в долг под сложную ссудную ставку 34% годовых.

Решение.

1. 
   используем формулу (3.2) при r=0,34; n=7/12:
   

1 января 2010 г. должник должен иметь 337 220 руб.

2. 
   используем формулу (2.1) при r=0,34; n=5/12:
   

1 января 2011 г. должник должен иметь 451 870 руб.

3. 
   1 августа 2010 г. должник должен иметь 400 000 руб.
   

Задачи для подготовки к занятию

Задача 1. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25 % процента годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.

Задача 2. В банк вложены деньги в сумме 800 тыс. руб. на полтора года под 10% годовых с ежеквартальным начислением сложных процентов. Определите доход клиента в этой финансовой операции.

Задача 3. Банк предоставил ссуду в размере 500 тыс. руб. на 33 месяца под процентную ставку 28% годовых на условиях ежегодного начисления процентов. Какую сумму нужно будет вернуть банку по окончании срока при использовании следующих условиях: 1) при расчетах используется схема сложных процентов; б) при расчетах используется смешанная схема?
Задание на практическое занятие 3. Сложные ссудные ставки.

Контрольные вопросы

1. 
   Чему равен множитель наращения при начислении процентов по сложной ссудной ставке?
   
2. 
   Как соотносятся между собой наращенные суммы при начислении простых и сложных ссудных процентов?
   
3. 
   Верно ли, что начисление сложных процентов по ставке 12% годовых эквивалентно начислению сложных процентов по ставке 1% в месяц?
   
4. 
   Как пользоваться финансовыми таблицами при вычислении наращенной и приведенной стоимости?
   

Задача 1. Рассчитайте будущую стоимость 1000 долл. для следующих ситуаций:

1. 
   5 лет, 8% годовых, ежегодное начисление процентов;
   
2. 
   5 лет, 8 % годовых, полугодовое начисление процентов;
   
3. 
   5 лет , 8 % годовых, ежеквартальное начисление процентов.
   

Задача 2. За какой срок первоначальный капитал в 500 тыс. руб. увеличится до 2 млн. руб., если на него будут начисляться сложные проценты по ставке 10 % годовых?

Задача 3. Фирме нужно накопить 2 млн. долл., чтобы через 10 лет приобрести здание под офис. Наиболее безопасным способом накопления является приобретение безрисковых государственных ценных бумаг, генерирующих годовой доход по ставке 5 % годовых при полугодовом начислении процентов. Каким должен быть первоначальный вклад фирмы?

Задача 4. Рассчитать накопленную сумму, если на вклад в 2 млн. руб. в течение 5 лет начисляются непрерывные проценты с силой роста 10%.

Задача 5. Вы положили в банк на депозит 1000 долл.. Банк начисляет сложные проценты по схеме – за первый год 4% годовых, а затем ставка увеличивается на 1 % каждый год. Определить сумму, которая будет на Вашем счете через 4 года.

Задача 6. Банк предоставил ссуду в размере 10 000 долл. на 16 месяцев под 12 % годовых на условиях ежеквартального начисления процентов. Рассчитайте возвращаемую сумму при различных схемах процентов: 1) схема сложных процентов; 2) смешанная схема.