02 Электроника. Методические указания к самостоятельным занятиям по курсу электроники омск 2007 Министерство транспорта Российской Федерации

• Название: Методические указания к самостоятельным занятиям по курсу электроники омск 2007 Министерство транспорта Российской Федерации
• Дата: 17.06.2020
• Размер: 0.73 Mb.
• Имя файла: 02 Электроника.doc
• Тип: Методические указания; #130867
• страница: 3 из 5

2.1. Краткие теоретические сведения

Усилитель – это электронное устройство, управляющее потоком энергии, идущей от источника питания к нагрузке. Причем мощность, требующаяся для управления, как правило, намного меньше мощности, отдаваемой в нагрузку, а формы входного (усиливаемого) и выходного (на нагрузке) сигналов совпадают.

В усилительном каскаде на биполярном транзисторе, включенном по схеме с общим эмиттером (рис.15), в коллекторную цепь транзистора включен резистор R_к, с помощью которого формируется выходное напряжение.



Рис. 15. Схема транзисторного усилительного каскада с эмиттерной

стабилизацией рабочего режима

Делитель напряжения на резисторах R₁ и R₂ определяет значение тока базы I_б0, обеспечивающего положение рабочей точки покоя Р_т в режиме класса А. Для уменьшения влияния температуры на режим работы транзистора в цепь эмиттера включен резистор R_э, который осуществляет последовательную отрицательную обратную связь по постоянной составляющей. Конденсатор C_э исключает влияние отрицательной обратной связи по переменной составляющей (т. е. для полезного сигнала). Разделительный конденсатор C_р1 устраняет влияние внутреннего сопротивления источника входного сигнала U_вх на режим работы транзистора по постоянному току. Конденсатор C_р2 обеспечивает выделение из коллекторного напряжения переменной составляющей U_вых, которая может подаваться на нагрузочный резистор R_н.
2.2. Методические указания
2.2.1. Записать параметры заданного транзистора, изобразить схему усилительного каскада (см. рис. 15) и объяснить назначение каждого элемента схемы.

2.2.2. Перечертить входную характеристику I_б = f (U_бэ) при U_кэ = – 5 В и семейство выходных вольт-амперных характеристик I_к = f (U_кэ) при I_б = const, на которых по нескольким точкам построить кривую допустимой мощности P_к = I_кU_к= P_доп, рассеиваемой транзистором (рис. 16). Ниже этой кривой из точки U_кэ = E_к, выбрав наиболее подходящий угол наклона, провести нагрузочную линию U_кэ = E_к – I_к(R_к+R_э), на которой выбрать и отметить положение рабочей точки покоя Р_т в режиме класса А и допустимые при этом пределы изменения амплитуды базового тока ±I_mб, соответствующие максимальному значению входного сигнала. Положение рабочей точки на входной характеристике должно соответствовать значению тока I_б0, при котором выбрана рабочая точка на пересечении линии нагрузки и выходной характеристики.

2.2.3. На графиках выходных и входной характеристик изобразить (подобно рис. 16) кривые i_к = I_к0 + I_m кsin(t), u_кэ =U_кэ0 + U_m кэsin(t), i_б = I_б0 + I_m бsin(t).

По графикам определить и записать значения: I_б0; ±I_m б = ±0,5 (I_б max– – I_б min); I_к0; ±I_m к= ±0,5 (I_к max–I_к min); I_э0= I_б0+I_к0; U_бэ0; ±U_m бэ= ±U_m вх; U_кэ0; ±U_m кэ= ±U_m вых= ±0,5(U_кэ max–U_кэ min).

2.2.4. Рассчитать значения h_э-параметров для схемы с общим эмиттером:

h11э= h11б/ (1+h21б); (23) h12э= (h11бh22б– h12бh21б– h12б) / (1+h21б); (24)

h21э= – h21б / (1+h21б); (25) h22э=h22б / (1+h21б). (26)

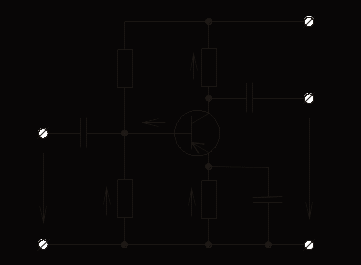
Для схемы включения транзистора с общим эмиттером определить входное сопротивление транзистора r_{вх транз} = h_11э и коэффициент передачи тока
 = h_21э.



а



б

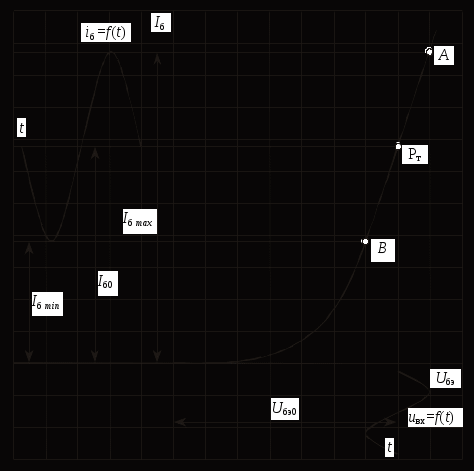
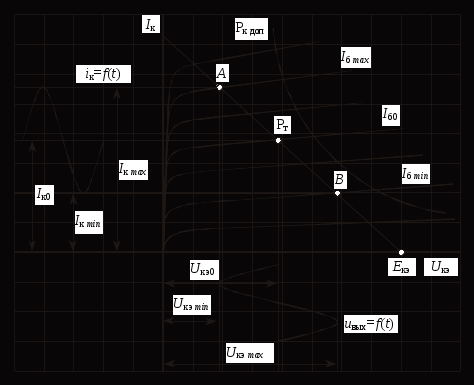
Рис. 16. Определение рабочего режима транзистора по входной характеристике (а) и по семейству выходных характеристик (б)

2.2.5. Рассчитать значения сопротивлений резисторов и емкостей конденсаторов:

R_э= (0,2,…,0,3) E_к / I_э0. (27)

Задавшись значением сопротивления R₁= (2,…,5) r_{вх транз}, определить

I_дел= (I_э0R_э + U_бэ0) / R₁; (28)

R₂ = (E_к – I_делR₁) / (I_дел + I_б0); (29)

R_к = (E_к – U_кэ0– I_э0R_э) / I_к0, (30)

или принять I_дел= (2,…,5) I_б0 и найти

R₁= (I_э0R_э + U_бэ0) / I_дел; (31)

R₂ = (E_к – I_делR₁) / (I_дел + I_б0); (32)

R_к = (E_к – U_кэ0– I_э0R_э) / I_к0. (33)

Эквивалентное сопротивление базовой цепи для переменной состав-ляющей входного тока

R_б = R₁R₂ / (R₁+R₂). (34)

Значения емкости конденсаторов при частотной полосе входного сигнала в пределах f_н = 100 Гц, f_в = 10000 Гц определяются так:

C_э= 10⁷ / [(1,…,2)2f_нR_э]; (35)

C_р1= C_р2= 10⁷ / [(1,…,2)2f_нR_{каск вх}], (36)

где C_э, C_р1 и C_р2 – в мкФ.

2.2.6.Определить параметры усилительного каскада.

Входное и выходное сопротивления каскада определяются следующим образом:

R_{каск вх} = R_бr_{вх транз} / (R_б + r_{вх транз}); (37)

R_{каск вых}= R_к / (1 + h_22эR_к). (38)

Коэффициенты усиления каскада без дополнительной внешней нагрузки, а также без учета внутреннего сопротивления источника входного сигнала имеют вид:

K_I= I_вых / I_вх  ; (39)

K_U= – (R_к) / R_{каск вх}; (40)

K_P= K_IK_U. (41)

Полезная выходная мощность каскада

P_вых = 0,5 (U_mвых)² / R_к. (42)

Полная мощность, расходуемая источником питания,

P₀ = I_э0E_к + I²_дел(R₁ + R₂) + I²_б0R₂. (43)

Электрический КПД усилительного каскада

_э = (P_вых / P₀) 100%. (44)

Коэффициент нестабильности каскада по коллекторному току (желательно, чтобы он был меньше)

S =  / (1+) или S  1+ R_б / R_э, (45)

S  (R_б + R_э) / [(1+h_21б) R_б + R_э], (46)

где  = R_э / (R_б + R_э).

3. СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ

Цель работы: изучить принципы функционирования логических элементов, научиться минимизировать логические функции алгебраическим методом и с помощью карт Карно, а также реализовывать цифровые комбинационные схемы в различных базисах.

3.1. Краткие теоретические сведения

Логические (цифровые) схемы составляют основу устройств цифровой (дискретной) обработки информации – вычислительных машин, цифровых измерительных приборов и устройств автоматики. Связи между этими схемами строятся на основе исключительно формальных законов. Инструментом такого построения и анализа служит булева алгебра, которая применительно к цифровой технике называется алгеброй логики.

Введем основные понятия алгебры логики.

Логическая переменная – это переменная, которая может принимать только два значения, которые обычно называются логическим нулем (0) и логической единицей (1).

Логическая функция – логическая (зависимая) переменная, значение которой является функцией одной или нескольких логических (независимых) переменных.

Таблица истинности – таблица, в которой заданы значения логической функции для всех возможных значений независимых переменных.

Существуют три основные логические функции:

1) логическое отрицание, или инверсия, обозначаемая чертой над выражением функции либо аргументом: (табл. 5) и именуемая функцией НЕ;

2) логическое умножение, или конъюнкция, показываемая знаками «Ù», «», «&» или «*»: (табл. 6). Отметим, что данная функция равна логической единице только тогда, когда оба аргумента равны единице, поэтому операцию конъюнкции называют функцией И;

3) логическое сложение, или дизъюнкция, обозначаемая знаками «» или «+»: (табл. 7). При дизъюнкции двух переменных функция равна логической единице тогда, когда хотя бы один из аргументов равен единице, поэтому дизъюнкцию называют функцией ИЛИ.

Кроме основных логических функций существуют также логические функции, базирующиеся на основных, которые часто используются в алгебре логики:

1) ИЛИ-НЕ: ;

2) И-НЕ: ;

3) равнозначность: ;

4) неравнозначность: .

Табл. 8 – 11 – таблицы истинности этих функций.
Таблица 5 Таблица 6 Таблица 7

X	Y		X1	X2	Y		X1	X2	Y
0	1		0	0	0		0	0	0
1	0		0	1	0		0	1	1
			1	0	0		1	0	1
			1	1	1		1	1	1

Таблица 8 Таблица 9 Таблица 10 Таблица 11

ИЛИ-НЕ И-НЕ Равнозначность Неравнозначность

X1	X2	Y		X1	X2	Y		X1	X2	Y		X1	X2	Y
0	0	1		0	0	1		0	0	1		0	0	0
0	1	0		0	1	1		0	1	0		0	1	1
1	0	0		1	0	1		1	0	0		1	0	1
1	1	0		1	1	0		1	1	1		1	1	0

Применительно к логическим операциям в алгебре логики существуют следующие законы:

1) переместительный: ; ;

2) сочетательный:

; ;

3) распределительный:

; ;

4) поглощения: ; ;

5) склеивания: ; ;

6) теорема де Моргана: и ;

Помимо приведенных законов применяют также следующие правила:

1) повторения: или

2) отрицания: или ;

3) двойного отрицания:

4) операций с нулем и единицей: ; ; ; ; ; .

Отметим, что некоторые из этих законов и правил известны из алгебры чисел, остальные для чисел несправедливы, а понятие «отрицание» для чисел вообще не определено.

Функция алгебры логики считается полностью определенной, если заданы ее значения для всех сочетаний аргументов. К способам задания функций относят:

1) табличный – когда функция представляется таблицей истинности (соответствия), содержащей 2ⁿ строк и (n+ 1) столбцов для n аргументов. В последнем (n + 1)-м столбце находятся значения функции, соответствующие сочетанию значений аргументов, записанных в первых n столбцах. Структура таблицы истинности для трех аргументов приведена на рис. 17;

2) алгебраический – функция представляет собой алгебраическое выражение, в котором определен порядок выполнения логических операций над аргументами, например: или ;

3


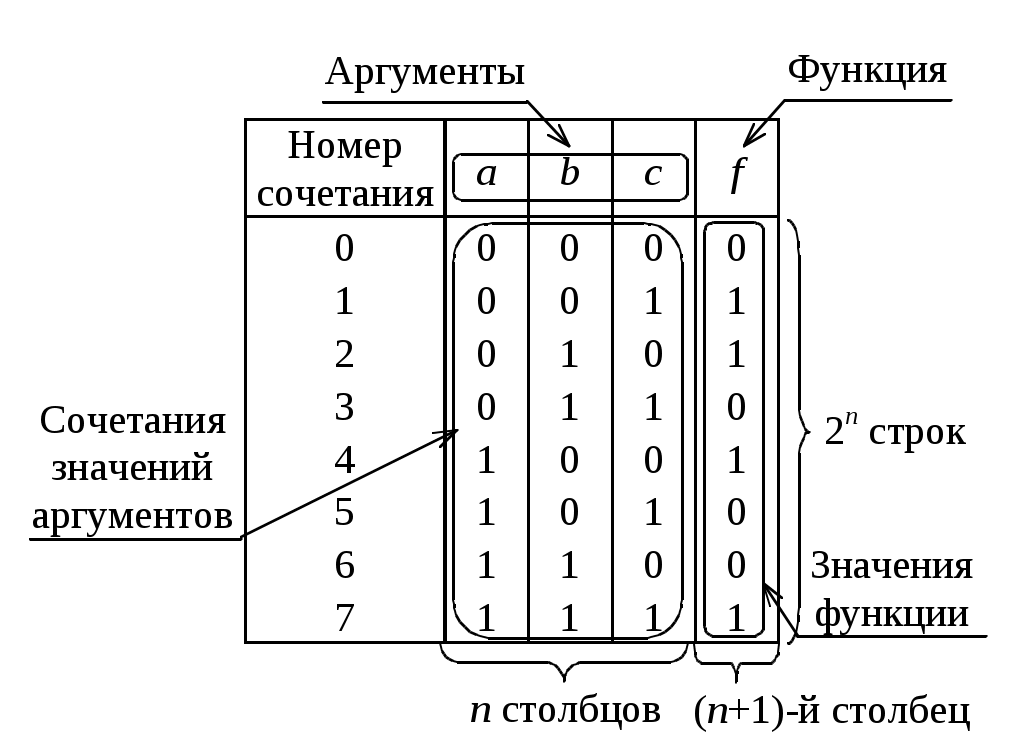
Рис.17. Таблица истинности функции f(a, b, c)

для n = 3


) числовой – функция задается номерами наборов, для которых значение функции равно единице. В соответствии с этим для функции, приведенной на рис. 17, можно записать следующее: f= {1, 2, 4, 7} a, b, c. Для функций, имеющих безразличные или неопределенные состояния на некоторых наборах данных, в таблице истинности проставляются знаки «», «» или «*», а в числовом способе записи через дробь указываются эти номера сочетаний, например: f = {1, 2, 3/5, 7} a, b, c. Другой вариант записи функции предполагает указание обязательных и запрещенных сочетаний в следующем виде: f = {1, 2, 3, (0, 4, 6)} a, b, c. В обоих случаях функция равна единице на наборах 1, 2, 3, имеет безразличное состояние в сочетаниях 5 и 7, а в остальных случаях (0, 4, 6) равна нулю;

4) координатный – функция задается в виде координатной карты состояний (карты Карно), содержащей 2ⁿ клеток, где в каждой клетке содержится значение функции для определенного сочетания значений аргументов. На рис. 18, а представлена карта для функции f(a, b, c) (см. рис. 17). На рис. 18, б, в показаны карты для трех и четырех аргументов соответственно, где в каждой клетке вместо значения функции приведен номер сочетания аргументов.

Проставление координат карт производится произвольно, с учетом того, чтобы каждой клетке соответствовало одно сочетание значений аргументов таблицы истинности. Координатный вид задания удобен для логических функций не более чем пяти аргументов и служит для наглядного представления функции с целью проведения дальнейших преобразований и минимизации.

Каноническими формами представления логических функций являются дизъюнктивная (ДНФ) и конъюнктивная (КНФ) нормальные формы. Если каждое слагаемое (сомножитель) ДНФ (КНФ) содержит все аргументы функции, то такая форма является совершенной – СДНФ (СКНФ).



а б в

Рис. 18. Координатный способ задания функции

СДНФ может быть получена непосредственно из таблицы истинности, если представить в виде логических произведений наборы аргументов, на которых функция равна единице, а затем объединить их знаками логического сложения.

Для получения СКНФ из таблицы истинности необходимо представить в виде инверсий наборы аргументов, на которых функция принимает значение ноль, и объединить их знаками логического умножения.

По каноническим формам (СДНФ и СКНФ) могут быть построены логические устройства, но, как правило, схемы в этих случаях содержат избыточное количество элементов и, прежде чем их составить, функции должны быть упрощены и получены минимальные формы (МДНФ или МКНФ).

При минимизации функций алгебры логики, заданных перечисленными выше способами, могут быть использованы алгебраический (последовательный) метод и метод карт Карно.

Алгебраический метод минимизации основан на применении законов и правил алгебры логики для преобразования выражения функции с целью получения минимальной формы. При этом первоначальная запись функции может быть любой, а метод применим для любого числа аргументов.

Метод Карно применяется для небольшого числа аргументов (не более пяти) и основан на работе с координатной картой Карно (см. рис. 18), отличается простотой и наглядностью процесса минимизации.

При использовании метода Карно заданную функцию следует представить координатной картой и провести операции склеивания путем объединения в замкнутые области значений функции, равных единице или нулю, и исключить из выражения функции аргументы, изменяющие свои значения в пределах выделенных областей. Координатная карта представляет собой непрерывную поверхность, поэтому возможно объединение единиц, находящихся у противоположных границ карты. Функция запишется в минимальной дизъюнктивной нормальной форме, если операции склеивания проводились с наборами аргументов, на которых функция равна единице, и в минимальной конъюнктивной нормальной форме при проведении операций склеивания с наборами, на которых функция равна нулю. Следует помнить, что в одну область объединяются 2^k клеток, где k = 1, 2, 3 и т. д.

Логические функции могут быть реализованы с помощью соответствующих логических элементов, выполненных по технологии интегральных микросхем. Для упрощения разработки схем и анализа их работы приняты условные графические изображения для таких элементов, не раскрывающие внутреннее строение, а показывающие лишь логическую функцию элемента. Логические элементы, реализующие простейшие логические функции, показаны на рис. 19.
Рис. 19. Логические элементы

Интегральные микросхемы, реализующие логические функции, отличаются по потребляемой мощности, напряжению питания, значениям высокого и низкого уровня логических нуля и единицы, времени задержки распространения сигнала (быстродействию) и нагрузочной способности (коэффициент разветвления по выходу).

Интегральные микросхемы выполняются на основе различных логик: резистивно-транзисторной (РТЛ), диодно-транзисторной (ДТЛ), транзисторно-транзисторной (ТТЛ), эмиттерно-связанной (ЭСЛ), комплементарной МОП (КМОП) (с использованием полевых транзисторов с изолированным затвором).

Среди перечисленных наиболее распространенными являются логики ТТЛ и КМОП. Каждая из приведенных разновидностей логических схем позволяет наиболее просто реализовать одну из основных логических функций. Так, для логик РТЛ, ЭСЛ и КМОП это ИЛИ-НЕ; ДТЛ, ТТЛ – И-НЕ. Используя любой из этих базовых элементов (базис И-НЕ или ИЛИ-НЕ), можно получить остальные основные логические элементы, а следовательно, и любую логическую функцию.

В табл. 12 приведены способы получения схем, реализующих основные логические функции для базисов 2И-НЕ и 2ИЛИ-НЕ, где цифра обозначает количество входных линий логического элемента.

Таблица 12

Способы реализации основных логических функций

Базис
2И-НЕ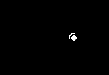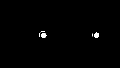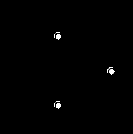
2ИЛИ-НЕ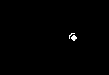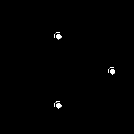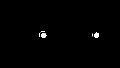