02 Электроника. Методические указания к самостоятельным занятиям по курсу электроники омск 2007 Министерство транспорта Российской Федерации
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
3.2. Задание для самостоятельной работы В соответствии с номером варианта из табл. 13 выбирается исходная функция, заданная в числовом виде, для которой необходимо выполнить следующее: 1) представить заданную функцию таблицей истинности; 2) записать СДНФ и СКНФ; 3) минимизировать функцию алгебраическим методом; 4) составить карту Карно; 5) минимизировать функцию методом карт Карно; 6) реализовать функцию на логических элементах базисов И-ИЛИ-НЕ, И-НЕ и ИЛИ-НЕ. Таблица 13 Варианты задания функций
3.3. Пример расчета Рассмотрим пример для функции, заданной в виде f = {2, 4, 6} a,b,c. 1 Таблица 14 Таблица истинности функции f = {2, 4, 6} a,b,c  ) Составляем таблицу истинности для данной функции. Заполняем столбцы аргументов a,b,c числовыми значениями в порядке возрастания номеров наборов в двоичном коде. Поскольку в числовом выражении функции присутствуют только номера сочетаний, соответствующие единичным значениям функции, то это позволяет проставить логические единицы для наборов 2, 4 и 6, а логические нули – для сочетаний 0, 1, 3, 5 и 7 (табл. 14). 2) Для записи СДНФ из таблицы истинности выбираем те строки, в которых значение функции равно единице. Для каждой такой строки составляем конъюнкцию всех входных переменных, записывая сомножитель, если эта переменная принимает значение единицы. Записываем логическую сумму всех найденных произведений и приходим к выражению вида: Для записи СКНФ из таблицы истинности выбираем строки, в которых значение функции равно нулю, инвертируем аргументы и получаем: 3) Учитывая законы алгебры логики, упрощаем выражение СДНФ функции. Используем распределительный закон для суммы произведений, выносим за скобки общие множители: Применяя правило отрицания, согласно которому сумма прямого и инверсного значения переменной a в скобках равна единице, запишем функцию в виде: Для дальнейших преобразований используем распределительный закон для произведения сумм логических переменных: И окончательно, применяя правило отрицания для суммы прямого и инверсного значений переменной b, записываем выражение: 4) Составляем карту Карно для функции f. Поскольку имеется три аргумента (a, b, c), то карта содержит 23 = 8 клеток. Обозначаем координаты a, b, c карты, проставляем единицы в клетки, соответствующие 2, 4 и 6 наборам (используем выражение СДНФ, полученное ранее), во все остальные клетки записываем нули (рис. 20, а). 5) Минимизация функции, заданной в виде координатной карты, предполагает склеивание четного количества (2, 4 и 8) находящихся рядом единиц для получения МДНФ, причем чем больше единиц будет объединено, тем более компактную алгебраическую запись будет иметь функция. Объединяемые единицы выделяем графически на карте, как показано на рис. 20, б. Полученные произведения аргументов записываем в виде слагаемых МДНФ с последующим вынесением за скобки общего множителя:   а б Рис. 20. Карты Карно: а – заполнение исходной карты; б – минимизация карты 6) Реализуем полученную функцию на логических элементах базисов И-ИЛИ-НЕ (рис. 21, а), ИЛИ-НЕ (рис. 21, б) и И-НЕ (рис. 21, в), используя известные способы реализации основных логических функций (табл. 15).  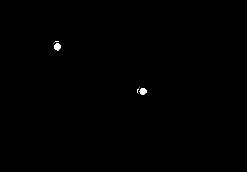 а б 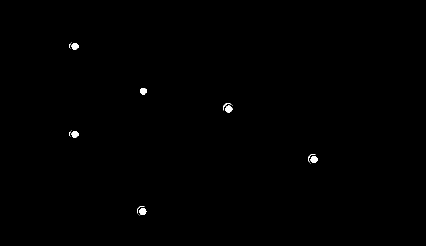 в Рис. 21. Реализация функции f(a, b, c) в различных базисах ПРИЛОЖЕНИЕ 1 ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
