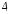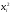математическая статисика Методичка для расчетов. Методические указания к выполнению индивидуальных типовых расчетов по математической статистике
 Скачать 421.46 Kb. Скачать 421.46 Kb.
|
1 2 Методические указания к выполнению индивидуальных типовых расчетов по математической статистике (электронная версия) На конкретном примере (выборочные данные) дана методика выполнения типовых расчетов по темам: Построения интервального статистического ряда распределения (типовой расчет №1). Вычисление выборочных характеристик ряда распределения (типовой расчет №2). Графическое изображение рядов распределения (типовой расчет №3). Расчет теоретической нормальной кривой распределения (типовой расчет №4). Проверка гипотеза о нормальном законе распределения по критерию согласия Пирсона χ2 (типовой расчет №5). Задание. По выборочным данным, представленным в таблице №11-38, требуется выполнить типовые расчеты: Типовой расчет №1: Построить интервальный статистический ряд распределения. Типовой расчет №2: Вычислить выборочные характеристики статистического ряда: начальные моменты 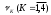 , среднюю арифметическую , среднюю арифметическую 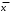 , центральные моменты , центральные моменты 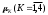 , дисперсию , дисперсию 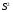 , среднее квадратическое отклонение S , коэффициенты ассиметрии , среднее квадратическое отклонение S , коэффициенты ассиметрии 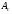 и эксцесса и эксцесса 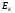 , медиану , медиану 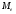 , моду , моду 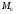 , коэффициент вариации , коэффициент вариации 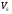 . .Дать экономическую интерпретацию выборочным числовым характеристикам. Типовой расчет №3: Построить гистограмму, полигон, кумуляту, огиву. Сделать вывод о форме ряда распределения по виду гистограммы и полигона, а также по значениям коэффицицентов 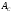 и и 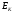 . .Типовой расчет №4: Рассчитать теоретическую нормальную кривую распределения 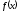 и построить ее на эмпирическом графике. и построить ее на эмпирическом графике.Сделать вывод о согласовании между теоретическим и эмпирическим распределениями. Типовой расчет №5: Проверить гипотезу о нормальном законе распределения по критерию согласия Пирсона ( 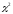 ) на заданном уровне значимости α = 0,05. ) на заданном уровне значимости α = 0,05.Типовой расчет №1 Построение интервального статистического (вариационного) ряда распределения. Дана выборка обследования 100 однотипных предприятий получены данные объема основных фондов (табл.1.1). Таблица I.I Объем основных фондов 100 (млн. руб.) предприятий легкой промышленности
Этапы построения интервального статистического (вариационного) ряда распределения. 1. Определение среди имеющихся наблюдений (табл.1.1) минимального Хmin. и максимального Хmах значения признака. В данном примере это будут 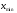 =5,03 и =5,03 и 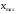 =5,85. =5,85.Определение размаха варьирования признака R = 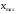 - -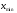 = 5,85 - 5,03 = 0,82 = 5,85 - 5,03 = 0,82Определение длины интервала по формуле h = 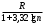 , где n - объем выборки. , где n - объем выборки. В данном примере h = 0.82/1+3.32 lg100=0.11 Определение граничных значений интервалов ( 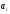 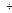 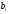 ). ). Так, как 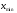 и и 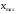 являются случайными величинами, рекомендуется отступить влево от нижнего предела варьирования ( являются случайными величинами, рекомендуется отступить влево от нижнего предела варьирования (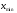 ). ).За нижнюю границу первого интервала предлагается принимать величину, равную 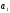 = =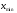 –h/2. –h/2.Если оказывается, что 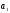 < 0 , хотя по смыслу величина не отрицательная, то можно принять < 0 , хотя по смыслу величина не отрицательная, то можно принять 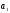 = 0. = 0.Верхняя граница первого интервала 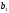 = = 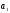 +h. Тогда, если +h. Тогда, если 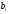 – верхняя граница i-го интервала (причем – верхняя граница i-го интервала (причем 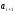 = =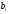 ), то ), то 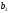 = =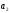 +h, +h, 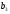 = =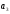 +h и т.д. Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет равным или больше +h и т.д. Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет равным или больше 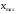 . .В примере граничные значения составят: 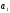 =5.03-0.11/2=4.97; =5.03-0.11/2=4.97; 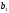 =4.97+0.11=5.08; =4.97+0.11=5.08; 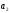 =5.08; =5.08; 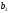 =5.08+0.11=5.19 и т.д. =5.08+0.11=5.19 и т.д.Границы последовательных интервалов записывают в графе I таблицы 1.2. Группировка результатов наблюдения. Просматриваем статистические данные в том порядке, в каком они записаны в таблице I.I, и значения признака разносим по соответствующим интервалам, обозначая их так: (по одному штриху для каждого наблюдения). Так как граничные значения признака могут совпадать с границами интервалов, то условимся в каждый интервал включать варианты, большие, чем нижняя граница интервала ( 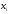 > >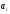 ), и меньшие или равные верхней границе ( ), и меньшие или равные верхней границе (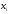 < <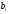 ). Общее количество штрихов, отмеченных в интервале (табл.1.2, графа 2) даст его частоту (табл. 1.2, графа 3). В результате получим интервальный статистический ряд распределения частот (табл.1.2 графа I и 3). ). Общее количество штрихов, отмеченных в интервале (табл.1.2, графа 2) даст его частоту (табл. 1.2, графа 3). В результате получим интервальный статистический ряд распределения частот (табл.1.2 графа I и 3).Примечание. Число интервалов обычно берут равным от 7 до 11 в зависимости от числа наблюдений и точности измерений с таким расчётом, чтобы интервалы были достаточно наполнены частотами. Если получают интервалы с нулевыми частотами, то нужно увеличить ширину интервала (особенно в середине интервального ряда). Таблица 1.2 Интервальный ряд распределения объемов основных фондов 100 предприятий
Соответствие между 1 и 3 столбцами является интервальным вариационным рядом абсолютных частот. Вопросы для самопроверки В чем отличие генеральной совокупности от выборочной совокупности? Что называется статистическим (вариационным) рядом распределения? Виды рядов распределения? Простой ряд и по сгруппированным данным? Как перейти от интервального вариационного ряда к дискретному ряду? В чем отличие абсолютной частоты от относительной частоты? Какие задачи решает теория вероятностей и математическая статистика? Типовой расчет №2 Вычисление выборочных характеристик статистического ряда распределения Для вычисления средней арифметической, дисперсии, коэффициентов асимметрии и эксцесса рекомендуется следующий порядок вычислений. Заменяем интервальный ряд дискретным для чего, все значения признака в пределах интервала приравниваем к его срединному значению, и считаем, что частота относится к середине интервала. Значения середин интервалов равны 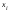 =( =(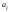 + +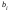 )/2. )/2.Для удобства вычислений целесообразно составить вспомогательную таблицу 1.3. Значения середин интервалов заносят в графу I, соответствующие частоты в графу 2 и т.д. В таблице ∆i = ( 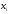 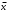 ) )Пользуясь таблицей 1.3, вычислим выборочную среднюю арифметическую: 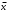 = =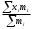 . .В нашем примере 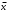 = 5,4656 млн.руб. и характеризует среднее положение наблюдаемых значений. = 5,4656 млн.руб. и характеризует среднее положение наблюдаемых значений.Выборочный центральный момент k-го порядка равен: 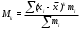 . .Таблица 1.3 Вспомогательная таблица для вычисления выборочных характеристик
Для проверки правильности вычисления 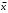 должно выполняться равенство: должно выполняться равенство: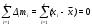 В нашем примере тождество выполняется. В итоговой строке столбца 4 табл.1.3 имеем 0 В данном примере 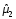 =0,028, =0,028, 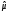 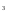 =-0,00088, =-0,00088, 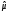 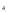 = 0,0022. = 0,0022.Выборочная дисперсия 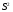 равна центральному моменту второго порядка: равна центральному моменту второго порядка: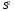 = =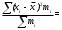 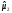 В нашем примере 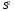 = 0,028. а выборочное среднее квадратическое отклонение S= = 0,028. а выборочное среднее квадратическое отклонение S=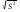 = 0,167 млн.руб. = 0,167 млн.руб.Выборочные коэффициенты асимметрии 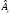 и эксцесса и эксцесса 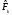 определяются по формулам определяются по формулам 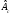 = =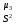 ; ;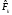 = =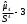 ; ;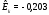 Медиана 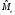 - значение признака x - значение признака x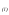 , приходящееся на середину ранжированного ряда наблюдений (n=2l-1). При четном числе , приходящееся на середину ранжированного ряда наблюдений (n=2l-1). При четном числе  наблюдений (n=2l) медианой наблюдений (n=2l) медианой 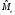 является средняя арифметическая двух значений, расположенных в середине ранжированного ряда: является средняя арифметическая двух значений, расположенных в середине ранжированного ряда: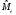 = =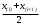 Если ранжировать значения, попавшие в медианные интервал [5,41;5,52], – интервал, в котором накопленная частота 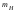 впервые превышает половину объема выборки впервые превышает половину объема выборки 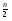 =50, – до значение =50, – до значение 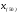 и и 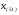 ,получим ,получим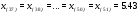 Следовательно, 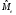 = =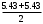 (млн.руб.). (млн.руб.).Если исходить из интервального ряда, то медиану следует вычислять по формуле 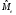 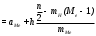 где 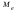 означает номер медианного интервала, ( означает номер медианного интервала, (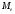 -1) - интервала, предшествующего медианному. -1) - интервала, предшествующего медианному.В нашем примере 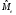 = 5,41+ = 5,41+ 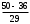 = 5,41+0,0531=5,46 млн.руб. = 5,41+0,0531=5,46 млн.руб.Мода 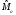 для совокупности наблюдений равна тому значению признака (табл.1.1), которому соответствует наибольшая частота. для совокупности наблюдений равна тому значению признака (табл.1.1), которому соответствует наибольшая частота.У нас вариант 5,43 имеет наибольшую частоту (m=15). Это означает, что 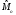 =5,43 млн.руб. =5,43 млн.руб.Для одномодального интервального ряда вычисление моды можно производить по формуле: 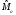 = =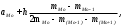 Где 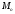 означает номер модального интервала (интервала с наибольшей частотой), означает номер модального интервала (интервала с наибольшей частотой), 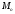 -1 и -1 и 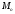 +1 – номера предшествующего модальному и следующего за ним интервалов. В нашем примере +1 – номера предшествующего модальному и следующего за ним интервалов. В нашем примере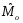 = 5,41 + = 5,41 + 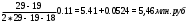 Так как 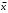 , , 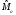 и и 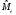 почти не отличаются друг от друга, есть основания предполагать теоретическое распределение нормальным. почти не отличаются друг от друга, есть основания предполагать теоретическое распределение нормальным.Коэффициент вариации: 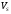 = =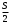 100%=3,06%. 100%=3,06%.Коэффициент вариации используют для характеристики того, насколько средняя арифметическая хорошо представляет статистический ряд распределения. Если ряды имеют одинаковые средние, то средняя арифметическая ряда с меньшим коэффициентом вариации более предпочтительна. Будучи безразмерным, 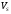 удобен для сравнений рядов распределения. удобен для сравнений рядов распределения.Типовой расчет №3 Графическое изображение вариационных рядов Для визуального подбора теоретического распределения, а также выявления положения среднего значения ( 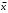 ) и характера рассеивания ( ) и характера рассеивания (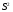 и S) вариационные ряды изображают графически. и S) вариационные ряды изображают графически.Полигон и кумулята применяются для изображения как дискретных, так и интервальных рядов, гистограмма - для изображения только интервальных рядов. Для построения этих графиков запишем вариационные ряды распределения (интервальный и дискретный) относительных частот (частостей) 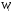 = =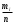 , накопленных относительных частот , накопленных относительных частот 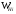 и найдем отношение и найдем отношение 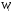 /h заполнив таблицу 1.4. /h заполнив таблицу 1.4.Таблица 1.4 Статистический ряд распределения объемов основных фондов 100 предприятий.
Для построения гистограммы относительных частот (частностей) на оси абсцисс откладываем частичные интервалы, на каждом из которых строим прямоугольник, площадь которого равна относительной частоте 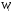 данного i-ого интервала. Тогда высота элементарного прямоугольника должна быть равна данного i-ого интервала. Тогда высота элементарного прямоугольника должна быть равна 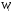 /h, где в нашем примере h= 0,11(рис.1.1). Следовательно, площадь под гистограммой равна сумме всех относительных частот, т.е. Единице. /h, где в нашем примере h= 0,11(рис.1.1). Следовательно, площадь под гистограммой равна сумме всех относительных частот, т.е. Единице.(Примечание: На рис.1.1 помимо гистограммы изображен график теоретической нормальной кривой f(x). Построение этого графика будет описано на стр. 9 данной методички) Из гистограммы можно получить полигон того же распределения, если середины верхних оснований прямоугольников соединить отрезками прямой (рис.1.2). Гистограмма и полигон являются аппроксимациями кривой плотности (дифференциальной функции) теоретического распределения (генеральной совокупности). Поэтому по их виду можно судить о гипотетическом законе распределения. Для построения кумуляты дискретного ряда по оси абсцисс откладывают значения признака 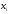 , а по оси ординат - накопленные относительные частота , а по оси ординат - накопленные относительные частота 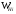 . Для интервального ряда по оси абсцисс откладывают интервалы (рис.1.3). . Для интервального ряда по оси абсцисс откладывают интервалы (рис.1.3).С кумулятой сопоставляется график интегральной функции распределения F(х). В нашем примере коэффициенты асимметрии и эксцесса не намного отличаются от нуля. Коэффициент асимметрии оказался отрицательным ( 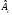 = - 0,188), что свидетельствует о небольшой левосторонней асимметрии данного распределения. Эксцесс оказался также отрицательным ( = - 0,188), что свидетельствует о небольшой левосторонней асимметрии данного распределения. Эксцесс оказался также отрицательным (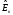 = -0,203). Это говорит о том, что кривая, изображающая ряд распределения, по сравнению с нормальной, имеет несколько более плоскую вершину. Гистограмма и полигон напоминают кривую нормального распределения (рис.1.1.и 1.2).Все это дает возможность выдвинуть гипотезу о том, что распределение объемов фондов является нормальным. = -0,203). Это говорит о том, что кривая, изображающая ряд распределения, по сравнению с нормальной, имеет несколько более плоскую вершину. Гистограмма и полигон напоминают кривую нормального распределения (рис.1.1.и 1.2).Все это дает возможность выдвинуть гипотезу о том, что распределение объемов фондов является нормальным.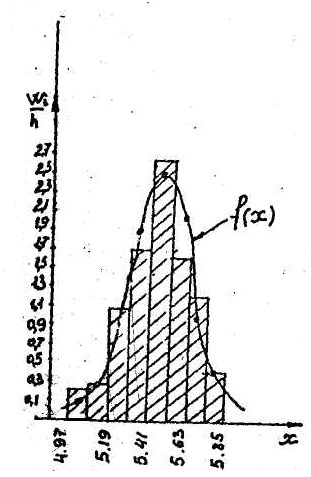 Рис. I.I. Гистограмма относительных частот интервального ряда распределения. 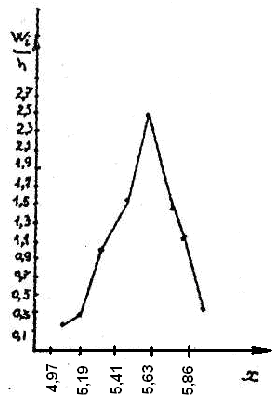 Рис.1.2. Полигон относительных частот интервального ряда распределения. 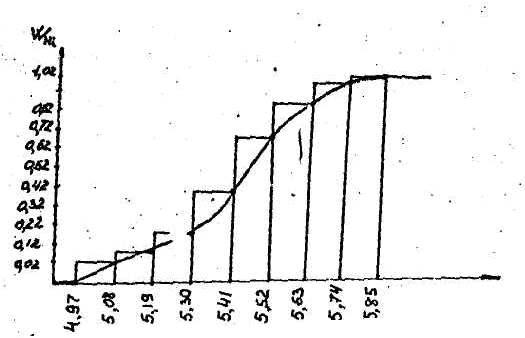 Рис. 1.3 Кумулятивная кривая. Типовой расчет №4 Расчет теоретической нормальной кривой распределения Приведем один из способов расчета теоретического нормального распределения по двум найденным выборочным характеристикам 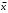 и S эмпирического ряда. и S эмпирического ряда.При расчете теоретических частот 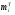 за оценку математического ожидания за оценку математического ожидания 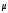 и среднего квадратического отклонения и среднего квадратического отклонения 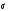 нормального закона распределения принимают значения соответствующих выборочных характеристик нормального закона распределения принимают значения соответствующих выборочных характеристик 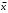 и S , т.е и S , т.е 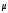 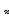 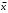 = 5,466; = 5,466; 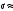 S =0,167. S =0,167.Теоретические частоты находят по формуле 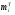 =n =n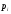 ; ; где n - объем выборки; 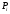 - вероятность попадания значения нормально распределенной случайной величины в i -й интервал. - вероятность попадания значения нормально распределенной случайной величины в i -й интервал. Вероятность 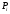 определяется по формуле определяется по формуле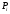 = =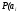 < <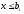 )=1/2 )=1/2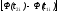 где Ф(t)= 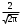 = =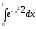 - интегральная функция Лапласа - находится по таблице для - интегральная функция Лапласа - находится по таблице для  = =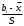 , , 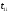 = =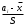 Для вычисления вероятности 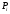 и теоретических частот и теоретических частот 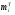 составим составим таблицу 1.5. Таблица 1.5 Расчет теоретической нормальной кривой распределения
Построим теоретическую нормальную кривую f(x) на рис.1.1. Для этого из середины частных интервалов восстановим перпендикуляры высотой 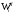 /h (табл.1.5, графа 10), где /h (табл.1.5, графа 10), где 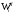 = =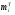 /n. На рис.1.1 концы этих перпендикуляров отмечены точками. Полученные точки соединены плавной кривой. /n. На рис.1.1 концы этих перпендикуляров отмечены точками. Полученные точки соединены плавной кривой. Рис. I.I. Гистограмма относительных частот интервального ряда распределения. Сравнение гистограммы и теоретической нормальной кривой 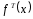 наглядно показывает согласованность между теоретическим и эмпирическим распределениями. наглядно показывает согласованность между теоретическим и эмпирическим распределениями.Типовой расчет №5 Проверка гипотезы о нормальном законе распределения Примечание. При использовании критерия согласия Пирсона общее число наблюдений должно быть достаточно большим (n>50) и интервалы должны быть достаточно заполнены частотами. Если отдельные теоретические частоты на концах распределения окажутся малыми ( 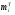 <5), <5),то при вычислении 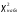 необходимо объединить такие интервалы, сложив соответствующие частоты. необходимо объединить такие интервалы, сложив соответствующие частоты.Частоты для проверки соответствия эмпирического ряда распределения нормальному закону используют критерий 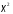 , основанный на сравнении эмпирических частот , основанный на сравнении эмпирических частот 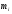 с теоретическими с теоретическими 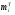 , которые можно ожидать при принятии определенной нулевой гипотезы. , которые можно ожидать при принятии определенной нулевой гипотезы.Значение 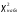 - наблюдаемое значение критерия, полученное по результатам наблюдений, равно - наблюдаемое значение критерия, полученное по результатам наблюдений, равно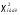  = =где к - число интервалов (после объединения), 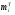 – теоретические частоты. Все вспомогательные расчеты, необходимые для вычисления – теоретические частоты. Все вспомогательные расчеты, необходимые для вычисления 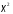 , сведем в таблицу 1.6. , сведем в таблицу 1.6. 1 2 |