Задачник по гидродинамике. Методические указания к выполнению контрольных и расчетнографических работ для студентов технических специальностей
 Скачать 1.65 Mb. Скачать 1.65 Mb.
|
|
Задача 2. Из открытого резервуара, в котором поддерживается постоянный уровень, по стальному трубопроводу (эквивалентная шероховатость 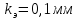 ), состоящему из труб различного диаметра ), состоящему из труб различного диаметра  и различной длины и различной длины 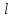 , вытекает в атмосферу вода, расход которой , вытекает в атмосферу вода, расход которой 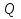 , температура , температура 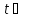 . Определить скорости движения воды, потери напора (по длине и местные) на каждом участке трубопровода, величину напора . Определить скорости движения воды, потери напора (по длине и местные) на каждом участке трубопровода, величину напора 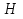 в резервуаре. Построить напорную и пьезометрическую линии на всех участках трубопровода. в резервуаре. Построить напорную и пьезометрическую линии на всех участках трубопровода.Решение задачи: Примем 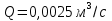 ; ; 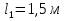 ; ; 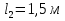 ; ; 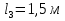 ; ;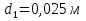 ; ; 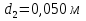 ; ; 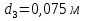 ; ; 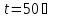 . .Составим уравнение Д. Бернулли для каждого из сечений: 0-0, 1-1, 2-2, 3-3: 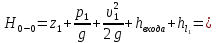 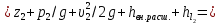 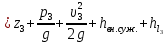 Из уравнения неразрывности 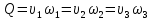 выразим выразим 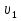 , , 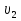 , , 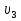 . .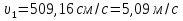 ( (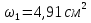 ); ); 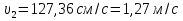 ( (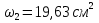 ); );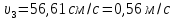 ( (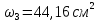 ). ).На первом участке трубопровода присутствуют местные потери на входе в трубу: 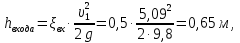 где 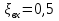 и потери напора по длине: и потери напора по длине: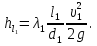 На втором участке трубопровода присутствуют местные потери на внезапное сужение: 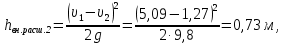 а потери напора по длине: 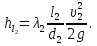 На третьем участке трубопровода присутствуют местные потери на внезапное сужение: 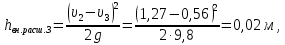 а потери напора по длине: 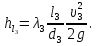 Для определения потерь напора по длине вычислим числа Рейнольдса и установим режим движения на каждом участке трубопровода. 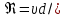 ( (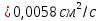 ), ),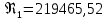 ; ; 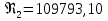 ; ; 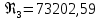 . .Значение 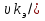 для первого участка составляет для первого участка составляет 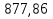 , для второго – , для второго – 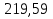 и для третьего – и для третьего – 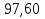 . . Следовательно, на первом участке имеет место квадратичная зона сопротивления, и значение 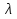 определяется по формуле Шифрисона: определяется по формуле Шифрисона: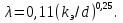 На втором и третьем участках трубопровод работает в переходной зоне сопротивления, в которой 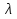 определяют по формуле Альтшуля: определяют по формуле Альтшуля: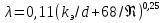 Следовательно, 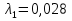 , , 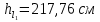 , , 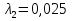 , , 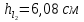 , , 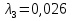 , , 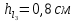 . .Величина напора составляет 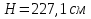 . .Напорная и пьезометрическая линии на всех участках трубопровода представлены на рис. 2.
Задача 3. Определить расход воды, проходящий через водоспускную трубу в бетонной плотине, если напор над центром трубы 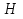 , диаметр трубы , диаметр трубы  , длина ее , длина ее 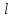 . .Решение задачи: Примем 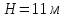 ; ; 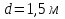 ; ; 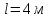 . .Расход воды, проходящий через водоспускную трубу, определим по формуле 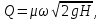 где 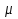 – коэффициент расхода; – коэффициент расхода; 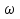 – площадь сечения трубы, – площадь сечения трубы, 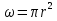 , , 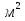 ; ; 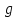 – ускорение свободного падения, – ускорение свободного падения, 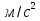 ; ; 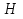 – напор над центром трубы, – напор над центром трубы, 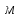 . .Чтобы труба работала как насадок и рассчитывалась как гидравлически короткий трубопровод, должны быть соблюдены одновременно два условия: 1) длина трубы должна быть 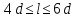 , , 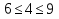 – условие не выполняется; – условие не выполняется;2) максимальный вакуум 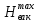 в насадке должен быть меньше 8 м вод. ст. Значение в насадке должен быть меньше 8 м вод. ст. Значение 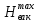 вычисляют по формуле вычисляют по формуле 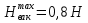 , где , где 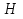 – напор над центром трубы. – напор над центром трубы. 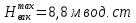 ., то есть условие не выполняется. ., то есть условие не выполняется. Водоспускная труба работает как отверстие и 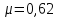 . .Расход воды составляет 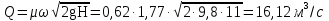 . .
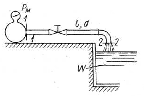
Задача 4. Определить время наполнения бассейна объемом 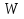 из магистрали с заданным давлением из магистрали с заданным давлением 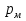 по горизонтальной трубе длиной по горизонтальной трубе длиной 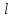 и диаметром и диаметром  , снабженной вентилем ( , снабженной вентилем (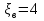 ) и отводом ( ) и отводом (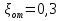 ) (рис.3). Коэффициент сопротивления трения определить по эквивалентной шероховатости ) (рис.3). Коэффициент сопротивления трения определить по эквивалентной шероховатости 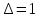 мм, предполагая наличие квадратичного режима. мм, предполагая наличие квадратичного режима.Решение задачи: Примем 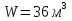 ; ; 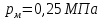 ; ; 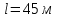 ; ; 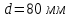 . .Напишем уравнение Бернулли для сечения 1-1 и 2-2 относительно оси трубопровода 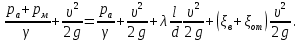 После приведения подобных членов получим 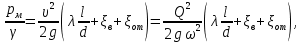 откуда 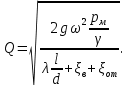 Коэффициент сопротивления трения определяем по формуле Никурадзе 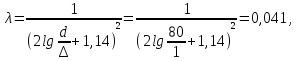 тогда 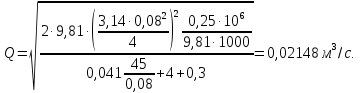 Время наполнения бассейна 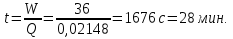
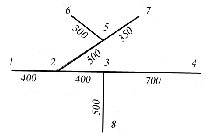
Задача 5. Определить диаметры труб для участков тупиковой водопроводной сети и установить требуемую высоту водонапорной башни в точке 1 для подачи следующих расходов в конечные пункты сети: 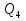 , , 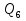 , , 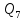 , и , и 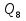 . Длины участков в метрах указаны на схеме сети (рис.4). Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор . Длины участков в метрах указаны на схеме сети (рис.4). Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор 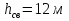 . При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб. . При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб.Решение задачи: Примем 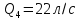 ; ; 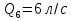 ; ; 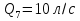 и и 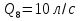 . .1. Устанавливаем расчетные расходы для всех участков сети: 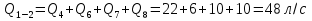 , ,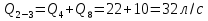 , ,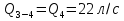 , ,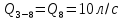 , ,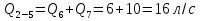 , ,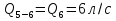 , ,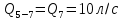 . .2. За главную линию тупиковой сети (магистраль) принимаем наиболее длинную и нагруженную линию, по которой проходят наибольшие расходы. В нашем случае за магистраль принимается линия 1-2-3-4. 3. Расчет магистрали ведем в данной последовательности: а) пользуясь табл. 1, определяем для заданных расчетных расходов диаметры труб для всех участков магистрали и заносим их в таблицу, в которую в дальнейшем будем заносить все результаты расчета магистрали; Таблица 1 – Значение предельных расходов и расходные характеристики для новых водопроводных труб
б) для принятых диаметров труб по справочной таблице находим расходные характеристики 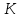 ; ;в) определяем потери напора на трение для каждого участка по формуле 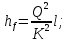 г) требуемую высоту водонапорной башни определяем из уравнения Бернулли, написанного для пунктов 1 и 4: 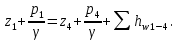 Так как местность по условию задачи горизонтальная, то 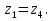 Пьезометрическая высота в первом пункте 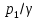 представляет собой искомую высоту водонапорной башни представляет собой искомую высоту водонапорной башни 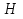 , а пьезометрическая высота , а пьезометрическая высота 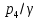 – свободный напор в конечном пункте – свободный напор в конечном пункте 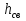 : :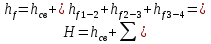 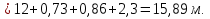 Округленно принимаем 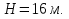 Определяем пьезометрические высоты в узлах магистрали: 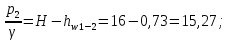 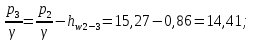 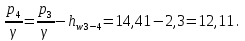 Таблица 2 – Результаты расчета магистрали
Окончание табл.2
4. Ответвления от магистрали делятся на простые и сложные. Простые ответвления состоят из одного участка, а сложные – из двух и более участков. В качестве сложного ответвления в нашем случае выбирается линия 2-5-7, так как участок 5-7 по длине больше, и расход 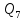 больше расхода больше расхода 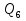 . .Расчет сложного ответвления ведется в определенной последовательности: а) определяем допустимые потери напора для ответвления 2-5-7 как разность пьезометрических высот в начальном и конечном пунктах ответвления: 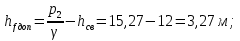 б) находим средний гидравлический уклон 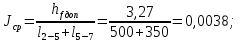 в) определяем требуемые расходные характеристики: 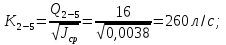 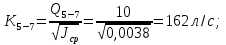 г) по справочным таблицам в соответствии со значениями требуемых расходных характеристик устанавливаем ближайшие диаметры стандартных труб: 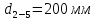 при при 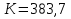 ; ;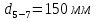 при при 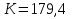 ; ;д) определяем фактические потери напора для принятых труб 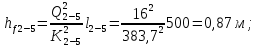 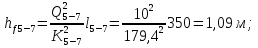 е) находим пьезометрические высоты 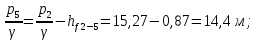 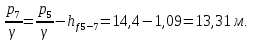 5. Расчет простых ответвлений 3-8 и 5-6 ведем в ниже излагаемой последовательности и результаты заносим в табл. 3: Таблица 3 – Результаты расчета ответвлений
а) определяем допустимые потери напора как разность пьезометрических высот в начальном и конечном пунктах 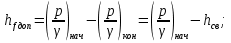 б) гидравлический уклон 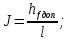 в) требуемая расходная характеристика 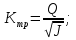 г) по справочной таблице устанавливаем ближайший больший диаметр стандартной трубы и его расходную характеристику 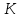 ; ;д) фактические потери напора 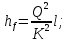 е) фактический свободный напор в конце ответвления 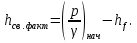
|

 ,
,  ,
, 