Методичка_ВЫЧМАТ. Методические указания к выполнению расчетнографической работы студентов очной формы обучения по направлениям подготовки
 Скачать 172.76 Kb.
|
|
Тема 5. Численное интегрирование Этот раздел посвящён построению и применению формул численного интегрирования, причём наибольшее внимание должно уделяться именно построению. Кроме лекционного материала и примеров, приводимых на практических занятиях, при построении формул можно использовать такие источники как [1], [7]. В некоторых вариантах построение формулы не требуется, а используется уже известная интерполяционно-квадратурная формула. В этих случаях нельзя использовать готовую составную формулу, а необходимо самому получать её с помощью линейной замены переменной. Точное значение интеграла должно быть вычислено аналитически и подробно записано, поскольку это также является частью работы. Задания РГР-5 Вариант 1. Построить ИКФ Ньютона-Котеса с четырьмя узлами и вычислить интеграл 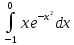 . Найти точное значение интеграла. Оценить погрешность. Вариант 2. Построить ИКФ Чебышева с тремя узлами и вычислить интеграл 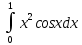 . Найти точное значение интеграла. Оценить погрешность. Вариант 3. Разбив отрезок на 4 части вычислить интеграл 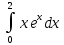 , используя формулу Симпсона на каждом отрезке. Найти точное значение интеграла. Оценить погрешность. Вариант 4. Построить ИКФ Гаусса с тремя узлами и вычислить интеграл 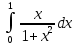 . Найти точное значение интеграла. Оценить погрешность. Вариант 5. Разбив отрезок на 2 части вычислить интеграл 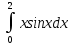 , используя формулу Чебышева с двумя узлами на каждом отрезке. Найти точное значение интеграла. Оценить погрешность. Вариант 6. Построить формулу Ньютона-Котеса с пятью узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 7. Разбив отрезок на 4 части вычислить интеграл  , используя формулу Гаусса с двумя узлами на каждом отрезке. Найти точное значение интеграла. Оценить погрешность.Вариант 8. Разбив отрезок на 5 частей вычислить интеграл  , используя а)формулу трапеций, б)формулу средних прямоугольников на каждом отрезке. Найти точное значение интеграла. Сравнить погрешность в обоих случаях. Вариант 9. Построить ИКФ Чебышева с четырьмя узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 10. Построить ИКФ Ньютона-Котеса с четырьмя узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 11. Построить ИКФ Чебышева с тремя узлами и вычислить интеграл 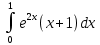 . Найти точное значение интеграла. Оценить погрешность. Вариант 12. Разбив отрезок на 5 частей вычислить интеграл 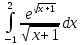 , используя формулу Симпсона на каждом отрезке. Найти точное значение интеграла. Оценить погрешность. Вариант 13. Построить ИКФ Гаусса с тремя узлами и вычислить интеграл 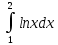 . Найти точное значение интеграла. Оценить погрешность. Вариант 14. Разбив отрезок на 4 части вычислить интеграл  используя формулу Чебышева с двумя узлами на каждом отрезке. Найти точное значение интеграла. Оценить погрешность.Вариант 15. Построить формулу Ньютона-Котеса с пятью узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 16. Разбив отрезок на 4 части вычислить интеграл  , используя формулу Гаусса с двумя узлами на каждом отрезке. Найти точное значение интеграла. Оценить погрешность. Вариант 17. Разбив отрезок на 10 частей вычислить интеграл  , используя а)формулу трапеций б) формулу средних прямоугольников на каждом отрезке. Найти точное значение интеграла. Сравнить погрешность в обоих случаях.Вариант 18. Построить ИКФ Чебышева с четырьмя узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 19. Построить ИКФ Ньютона-Котеса с пятью узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 20. Построить ИКФ Гаусса с тремя узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 21. Разбив отрезок на 5 частей вычислить интеграл  , используя формулу Симпсона на каждом отрезке. Найти точное значение интеграла. Оценить погрешность. Вариант 22. Построить ИКФ Гаусса с четырьмя узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 23. Разбив отрезок на 5 частей вычислить интеграл, используя формулу Чебышева с двумя узлами на каждом отрезке  . Найти точное значение интеграла. Оценить погрешность.Вариант 24. Построить формулу Ньютона-Котеса с пятью узлами и вычислить интеграл  . Найти точное значение интеграла. Оценить погрешность. Вариант 25. Разбив отрезок на 10 частей вычислить интеграл  , используя a) формулу правых прямоугольников, в) формулу средних прямоугольников на каждом отрезке. Найти точное значение интеграла. Оценить погрешность в каждом случае. Рекомендуемая литература 1. Амосов, А.А. Вычислительные методы: учеб. пособие для вузов/ А.А. Амосов, Ю.А.Дубинский, Н.В.Копчёнова. – СПб: Лань, 2014 -671 с. 2. Бахвалов, Н.С., Численные методы(анализ, алгебра, обыкновенные дифференциальные уравнения)/ Н.С.Бахвалов,– М: Наука, 1973.-632 с. 3.Бахвалов, Н.С. Численные методы: учеб. пособие для вузов/Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. –М: Бином, 2008.- 636 с. 4. Бахвалов, Н.С., Численные методы в задачах и упражнениях/ Н.С. Бахвалов, А.В.Лапин, Е.В. Чижонков Е.В. “ М.: Высшая школа, 2000 – 426 с. 5. Башмакова, М.Г. Численные методы линейной и нелинейной алгебры.: учеб. пособие/ М.Г. Башмакова. – Брянск, изд-во БГТУ, 2016 -128 с. 6.Волков, Е.А. Численные методы: учеб. пособие/ Е.А. Волков. – СПб: Лань, 2008. - 248 с. Режим доступа: http://e.landbook.com//books/element.php?p11_id=54 7. Демидович, Б.П. Основы вычислительной математики: учеб. пособие/Б.П. Демидович, И.А. Марон. – СПб: Лань, 2007. ̶ 664 с. ̶ Режим доступа: http://e.landbook.com//books/element.php?p11_id=2025 8.Жидков, Е.Н. Вычислительная математика: учеб. пособие для вузов/ Е.Н.Жидков. - М: Академия, 2010 - 208 с. 9.Калиткин, Н.Н. Численные методы/Н.Н.Калиткин. – СПб: BHV-2011.- 592 с. 10.Копчёнова, Н.В. Вычислительная математика в примерах и задачах/ Н.В. Копчёнова, И.А. Марон. – СПб:Лань, 2008. ̶ 368 с. ̶ Режим доступа: http://e.landbook.com//books/element.php?p11_id=198 11.Поршнев, С.В. Вычислительная математика: курс лекций. Учеб. пособие для вузов/ С. В. Поршнев. -СПб: BHV, 2004.-304 с. 12.Рябенький, В.С. Введение в вычислительную математику: учеб. пособие для вузов/В.С. Рябенький.- М: Физматлит, 2008. - 284 с. Вычислительная математика: методические указания к выполнению расчетно-графической работы студентов очной формы обучения по направлениям подготовки: 02.03.03 «Математическое обеспечение и администрирование информационных систем», 09.03.04 «Программная инженерия», 09.03.01 «Информатика и вычислительная техника» БАШМАКОВА МАРИЯ ГЕННАДЬЕВНА Научный редактор В.М. Кобзев Компьютерный набор М.Г. Башмакова Подписано в печать Формат 6084 1/16. Бумага офсетная Печать офсетная. Усл.печ. л. 1,39 Уч.-изд. л. 1,39. Брянский государственный технический университет 241035, г. Брянск, бульвар 50 лет Октября, 7, БГТУ Кафедра «Высшая математика», тел. 561477 |