Методичка_ВЫЧМАТ. Методические указания к выполнению расчетнографической работы студентов очной формы обучения по направлениям подготовки
 Скачать 172.76 Kb. Скачать 172.76 Kb.
|
 УТВЕРЖДАЮ Ректор университета __________О.Н. Федонин “____”___________2017 г ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА Методические указания к выполнению расчетно-графической работы студентов очной формы обучения по направлениям подготовки: 02.03.03 «Математическое обеспечение и администрирование информационных систем», 09.03.04 «Программная инженерия», 09.03.01 «Информатика и вычислительная техника» Брянск 2017 УДК 511 Вычислительная математика. [Электронный ресурс]: методические указания к выполнению расчетно-графической работы студентов очной формы обучения по направлениям подготовки: 02.03.03 «Математическое обеспечение и администрирование информационных систем», 09.03.04. «Программная инженерия», 09.03.01. «Информатика и вычислительная техника» – Брянск: БГТУ, 2017. – 24 с. Разработала: Башмакова М.Г., канд. физ.-мат. наук, доц. Рекомендовано кафедрой «Высшая математика» БГТУ (протокол №1 от 5.09.17) Методические указания публикуются в авторской редакции Предисловие Данные методические указания предназначены для подготовки и выполнения расчётно-графических работ по дисциплине «Вычислительная математика». В методичке приведены сами задания расчётно-графической работы, пояснения по оформлению и ссылки на литературу, позволяющие лучше понять данный метод. Расчётно-графическая работа состоит из нескольких задач, каждая из которых рассматривается в рамках определённой темы, изучаемой в курсе вычислительной математики. Студенту необходимо, выбрав вариант в соответствии со списком группы, разобраться с рассматриваемым методом и решить данную задачу, подробно записав способ решения. Следует заметить, что при выполнении РГР и при подготовке к её защите наиболее правильным является использования лекционного материала дисциплины и задач, разбираемых на практических занятиях. К дополнительной литературе нужно обращаться только после того, как этот материал был хорошо изучен. Тема 1. Решение систем линейных алгебраических уравнений методами Гаусса и Холецкого. Методы Холецкого и все модификации метода Гаусса являются прямыми методами решения систем линейных уравнений (СЛАУ). Эти методы требуют заранее известного числа шагов и потому довольно просты для реализации вручную. Достаточно разобраться в общей структуре метода, чтобы без труда решить задачу. При этом, тем не менее, необходимо подробно расписывать каждый шаг рассматриваемого метода, это должно помочь при защите РГР. Примеры оформления задач такого типа можно найти в [5]. Подробности и особенности таких прямых методов, как методы Гаусса и Холецкого можно найти в [7],[9],[12]. Задания РГР-1. Вариант 1. Решить систему методом Холецкого для матриц произвольного вида: 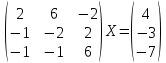 . .Вариант 2.Решить систему методом квадратных корней 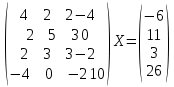 . .Вариант 3. Решить систему методом Гаусса с выбором главного элемента по столбцу: 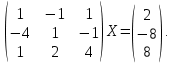 Вариант 4. Решить систему методом Гаусса с выбором главного элемента по матрице: 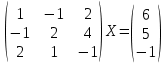 . .Вариант 5. Решить систему методом Холецкого с разложением на три матрицы. 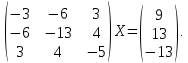 Вариант 6. Решить систему методом Жордана-Гаусса 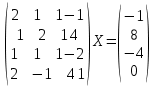 .. ..Вариант 7. Решить систему методом Гаусса с выбором главного элемента по столбцу: 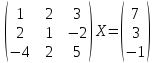 Вариант 8. Решить систему методом Гаусса с выбором главного элемента по матрице: 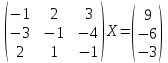 . .Вариант 9. Найти обратную матрицу методом Гаусса 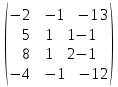 . .Вариант 10. Решить систему методом квадратных корней 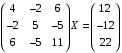 Вариант 11. Решить систему методом Холецкого для матриц произвольного вида 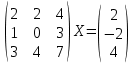 . .Вариант 12. Решить систему методом квадратных корней 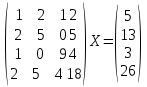 Вариант 13. Решить систему методом Гаусса с выбором главного элемента по столбцу 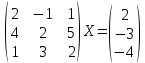 : :Вариант 14. Решить систему методом Гаусса с выбором главного элемента по матрице 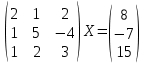 : :Вариант 15. Решить систему методом Холецкого для матриц произвольного вида 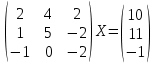 . .Вариант 16. Найти обратную матрицу методом Гаусса  . .Вариант 17. Решить систему методом Гаусса с выбором главного элемента по столбцу 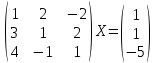 : :Вариант 18. Решить систему методом Гаусса с выбором главного элемента по матрице 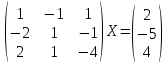 . .Вариант 19. Решить систему методом квадратных корней 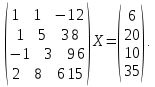 Вариант 20. Решить систему методом Холецкого для матриц произвольного вида 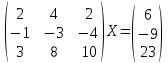 . .Вариант 21. Решить систему методом Жордана-Гаусса 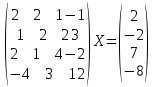 . .Вариант 22. Решить систему методом квадратных корней 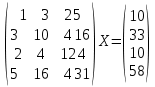 Вариант 23. Решить систему методом Гаусса с выбором главного элемента по столбцу 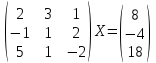 . .Вариант 24. Решить систему методом Гаусса с выбором главного элемента по матрице 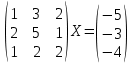 . .Вариант 25. Решить систему методом Холецкого с разложением на 3 матрицы 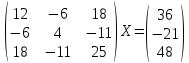 . .Тема 2. Другие методы решения систем линейных уравнений В этот раздел входят в основном итерационные методы, хотя есть и некоторые другие, такие как метод плоских вращений. Для итерационных методов в первую очередь следует разобраться с понятием сходимости и проверить условие сходимости в данном случае. Всю необходимую информацию о рассматриваемых алгоритмах, также как и способ оформления задач можно найти в [5]. Для получения дополнительных сведений воспользуйтесь [6],[8],[11]. Задания РГР-2 Вариант 1. Решить систему методом плоских вращений: 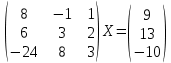 . .Вариант 2. Привести систему к нужному виду и найти решение методом простых итераций с точностью 0,1 и произвольным начальным приближением. Проверить решение подстановкой. Сделать выводы о сходимости метода простых итераций. 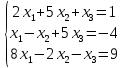 . .Вариант 3. Привести систему к нужному виду и решить методом Зейделя с точностью 0,1 и произвольным начальным приближением. Сделать выводы о сходимости метода Зейделя, проверить решение подстановкой: 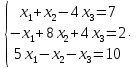 Вариант 4. Решить систему линейных уравнений методом Зейделя с точностью 0,1. 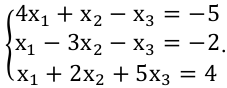 Вариант 5. Решить систему методом прогонки: 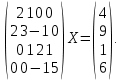 Вариант 6. Привести систему к нужному виду и решить методом простых итераций с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода простых итераций 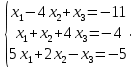 Вариант 7. Привести систему к нужному виду и решить методом Зейделя с произвольным начальным приближением и точностью 0.1. Проверить решение подстановкой, сделать выводы о сходимости метода Зейделя. 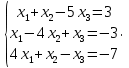 Вариант 8. Решить систему линейных уравнений методом простых итераций с точностью 0,1. 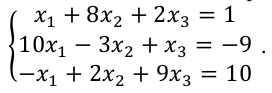 Вариант 9. Решить систему методом плоских вращений: 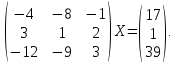 Вариант 10. Решить систему методом прогонки 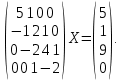 Вариант 11. Привести систему к нужному виду и решить методом простых итераций с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода простых итераций 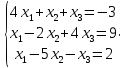 Вариант 12. Привести систему к нужному виду и решить методом Зейделя с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода Зейделя 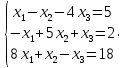 Вариант 13. Решить систему методом прогонки: 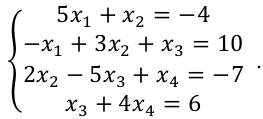 Вариант 14. Решить систему методом прогонки 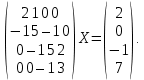 Вариант 15. Решить систему методом плоских вращений 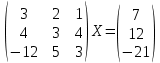 . .Вариант 16. Привести систему к нужному виду и решить методом простых итераций с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода простых итераций. 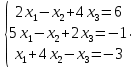 Вариант 17. Привести систему к нужному виду и решить методом Зейделя с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода Зейделя 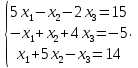 Вариант 18. Решить систему методом прогонки 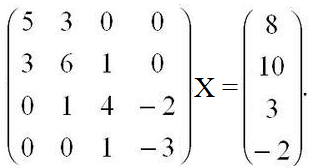 Вариант 19. Решить систему методом прогонки 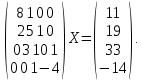 Вариант 20. Решить систему методом плоских вращений. 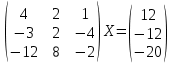 Вариант 21. Привести систему к нужному виду и решить методом простых итераций с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода простых итераций. 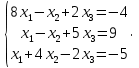 Вариант 22. Привести систему к нужному виду и решить методом Зейделя с произвольным начальным приближением и точностью 0,1. Проверить решение подстановкой, сделать выводы о сходимости метода Зейделя 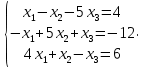 Вариант 23. Привести систему 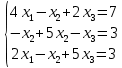 к нужному виду и решить методом простых итераций с точностью 0.1. к нужному виду и решить методом простых итераций с точностью 0.1.Вариант 24. Решить систему методом плоских вращений 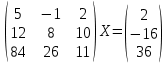 . . Вариант 25. Решить систему методом прогонки: 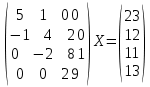 . .Тема 3. Методы решения нелинейных уравнений и систем Данная тема является достаточно объёмной, поскольку включает различные методы решения нелинейных уравнений, так и их систем. Для заданий, в которых требуется решить нелинейное уравнение, в расчётно-графической работе требуется также локализовать корень. Делать это необходимо вручную, используя аналитический или графический метод, но не применяя компьютерное построение графика, поскольку в этом случае работа теряет смысл. Способ локализации корня также должен быть описан в работе. Для заданий, в которых требуется решить систему, локализация корня уже задана. Полное решение такой задачи вручную потребовало бы значительных усилий, поэтому в этих заданиях не нужно решать пример данным методом до конца, а только сделать несколько шагов. Однако, этого достаточно чтобы разобраться с особенностями предлагаемого метода, его сходимостью и пошаговой реализацией. В случае, если в задании требуется найти точное решение системы, делать это нужно аналитически. Данная тема достаточно подробно рассматривается в [5], но также и в любом учебнике по вычислительной математике, рекомендуем, например [3],[6],[7]. Задания РГР – 3 Вариант 1. Локализовать корень уравнения 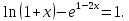 Привести уравнение к виду метода простых итераций, проверить условие сходимости, решить методом простых итераций с точностью ε=0.01. Привести уравнение к виду метода простых итераций, проверить условие сходимости, решить методом простых итераций с точностью ε=0.01.Вариант 2. Систему нелинейных уравнений 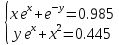 привести к виду метода простых итераций и сделать три шага этим методом, зная, что решение находится в квадрате [0,1]×[0,1]. Сделать выводы о сходимости метода итераций. привести к виду метода простых итераций и сделать три шага этим методом, зная, что решение находится в квадрате [0,1]×[0,1]. Сделать выводы о сходимости метода итераций.Вариант 3. Локализовать корень уравнения 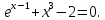 Методом секущих найти с точностью ε=0.01 решение уравнения. Проверить точность решения подстановкой. Методом секущих найти с точностью ε=0.01 решение уравнения. Проверить точность решения подстановкой.Вариант 4. Локализовать корень уравнения 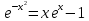 . Методом деления пополам найти корень с точностью ε=0.01. . Методом деления пополам найти корень с точностью ε=0.01.Вариант 5. Локализовать корень уравнения 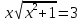 . Методом хорд найти корень с точностью ε=0.01. Проверить решение подстановкой. . Методом хорд найти корень с точностью ε=0.01. Проверить решение подстановкой.Вариант 6. Методом Ньютона найти с точностью ε=0.01 положительный корень уравнения 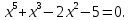 Вариант 7. Локализовать корень уравнения 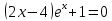 . Методом Ньютона найти корень с точностью ε=0.001. . Методом Ньютона найти корень с точностью ε=0.001. Вариант 8. Для системы нелинейных уравнений 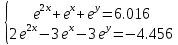 сделать два шага методом Ньютона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона. сделать два шага методом Ньютона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона.Вариант 9. Для системы нелинейных уравнений 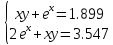 сделать три шага методом Ньютона-Рафсона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона-Рафсона. сделать три шага методом Ньютона-Рафсона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона-Рафсона.Вариант 10. 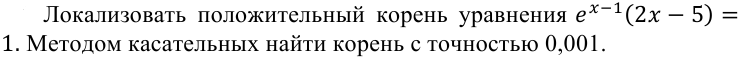 Вариант 11. Локализовать корень уравнения 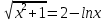 . Методом деления пополам найти корень с точностью ε=0.01. . Методом деления пополам найти корень с точностью ε=0.01.Вариант 12. Локализовать положительный корень уравнения 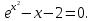 Методом хорд найти этот корень с точностью ε=0.01. Проверить решение подстановкой. Методом хорд найти этот корень с точностью ε=0.01. Проверить решение подстановкой. Вариант 13. 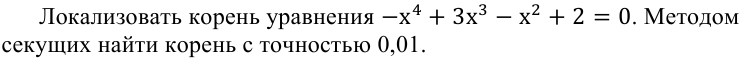 Вариант 14. Уравнение 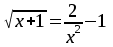 привести к виду метода простых итераций и найти этим методом отрицательный корень с точностью ε=0.01. Проверить условия сходимости метода простых итераций. привести к виду метода простых итераций и найти этим методом отрицательный корень с точностью ε=0.01. Проверить условия сходимости метода простых итераций.Вариант 15. Систему нелинейных уравнений 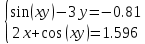 привести к виду метода простых итераций и сделать три шага этим методом, зная, что решение находится в квадрате [0,1]×[0,1]. Сделать выводы о сходимости метода итераций. привести к виду метода простых итераций и сделать три шага этим методом, зная, что решение находится в квадрате [0,1]×[0,1]. Сделать выводы о сходимости метода итераций.Вариант 16. Для системы нелинейных уравнений 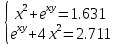 сделать два шага методом Ньютона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона. сделать два шага методом Ньютона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона.Вариант 17. Для системы нелинейных уравнений 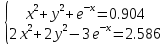 сделать три шага методом Ньютона-Рафсона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона-Рафсона. сделать три шага методом Ньютона-Рафсона, зная, что решение находится в квадрате [0,1]×[0,1]. Найти точное решение системы. Сделать выводы о сходимости метода Ньютона-Рафсона.Вариант 18. 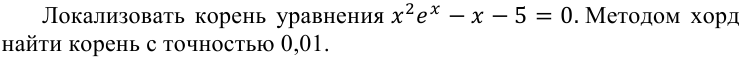 Вариант 19. Локализовать корень уравнения 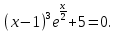 Методом Ньютона найти с точностью ε=0.001 корень уравнения Методом Ньютона найти с точностью ε=0.001 корень уравнения Вариант 20. Локализовать отрицательный корень уравнения 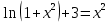 . Методом хорд найти этот корень с точностью ε=0.01. Проверить решение подстановкой. . Методом хорд найти этот корень с точностью ε=0.01. Проверить решение подстановкой.Вариант 21. Локализовать корень уравнения 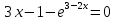 . Методом секущих найти с точностью ε=0.01 решение уравнения. Проверить точность решения подстановкой. . Методом секущих найти с точностью ε=0.01 решение уравнения. Проверить точность решения подстановкой.Вариант 22. Уравнение 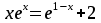 привести к виду метода простых итераций и найти положительный корень уравнения этим методом с точностью ε=0.01. Проверить выполнение условия сходимости метода итераций. привести к виду метода простых итераций и найти положительный корень уравнения этим методом с точностью ε=0.01. Проверить выполнение условия сходимости метода итераций.Вариант 23. Вариант 24.  Вариант 25. Найти положительный корень уравнения 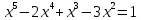 методом Ньютона с точностью ε=0.01.. методом Ньютона с точностью ε=0.01.. |
