щщ. БАЗДАРЕВА МУ раздела КНИР1 по курсу Анализ данных и аналитика в. Методические указания к выполнению раздела книр1 по курсу Анализ данных и аналитика в принятии решений
 Скачать 471.8 Kb. Скачать 471.8 Kb.
|
|
3.2. Временные ряды 3.2.1. Задачи анализа временных рядов Любое предприятие в процессе планирования своей деятельности сталкивается с необходимостью определить тенденции изменения основных экономических показателей. Задачи анализа временных рядов: описание характеристик и закономерностей ряда. На основе этого описания могут быть выявлены свойства соответствующих бизнес-процессов; моделирование исследуемого процесса; прогнозирование – предсказание будущих значений временного ряда; управление. Зная свойства временного ряда можно выработать методы воздействия на соответствующие бизнес-процессы. Если в течение достаточно продолжительного времени регулярно фиксировать курсы валют, акций, цены на товары и т.д., то такие данные образуют временные ряды. Временными рядами являются также данные о выпуске или потреблении различных товаров и услуг по месяцам, кварталам, годам. В производстве временные ряды возникают при измерении количества изделий, выпускаемых подразделениями предприятия за час, смену и т.д., при оценках количества брака за те же периоды, при наблюдении за изменениями запасов на складах. Практически все временные ряды социально-экономических процессов имеют изменчивый характер, колебания в большей или меньшей мере, что всегда заметно при их графическом представлении. Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда. Yt = f(t) +, - случайная составляющая, Yt - уровень ряда, f(t) – математическая функция, описывающая закономерность развития явления во времени (тенденцию развития во времени) – употребляют термин «тренд ряда». 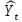 - теоретическое значение уровня ряда, соответствующее математической функции тренда. - теоретическое значение уровня ряда, соответствующее математической функции тренда.Поскольку зависимость от времени может принимать разные формы, для ее моделирования можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции: линейная, экспоненциальная, степенная, гипербола, параболическая и т.д. Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов. При прочих равных условиях предпочтение следует отдавать более простым функциям. Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой переменной -фактические уровни временного ряда Yt. Реализация этого метода относительно проста при компьютерной обработке данных. Основные этапы: выделить ключевые показатели функционирования системы; зафиксировать значения этих показателей за предшествующие периоды (не менее 10); оценить уравнение регрессии, характеризующее зависимость уровней ряда от времени; интерпретировать параметры модели; на основании построенной модели, дать прогноз значения показателя на ближайший период времени; 3.2.2. Пример к разделу 3.2. Известен объем сброса загрязненных сточных вод по бассейнам отдельных рек и морей Российской Федерации (млд.м3). Строится график зависимости, к которому добавляется линия тренда. В закладке Макет была выбрана кнопка Добавить линию тренда и отмечена линия линейного тренда. Были поставлены галочки у «Вывести на график уравнения тренда» и «Вывести коэффициент детерминации R2». 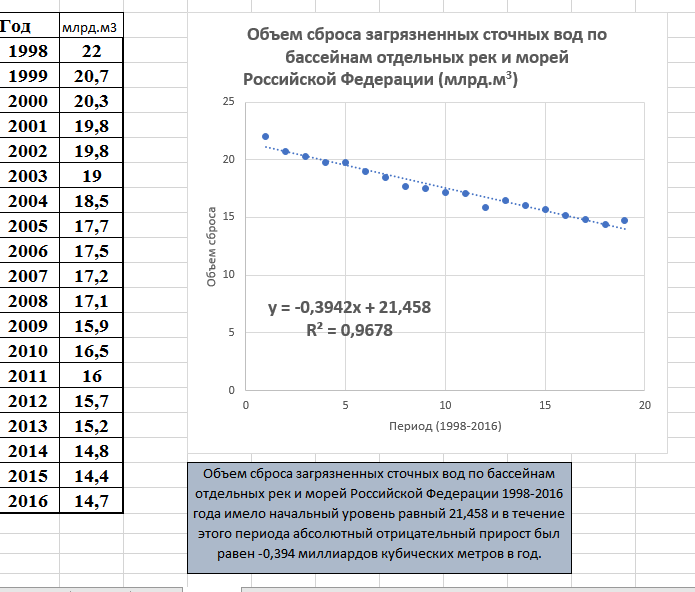 Для оценки параметров уравнения регрессии можно использовать также надстройку АНАЛИЗ ДАННЫХ. После выбора инструмента Регрессия в поле Y вводим данные для уровней ряда Yt, в поле Х вводим данные для переменной t, которую рассматриваем в качестве независимой переменной. 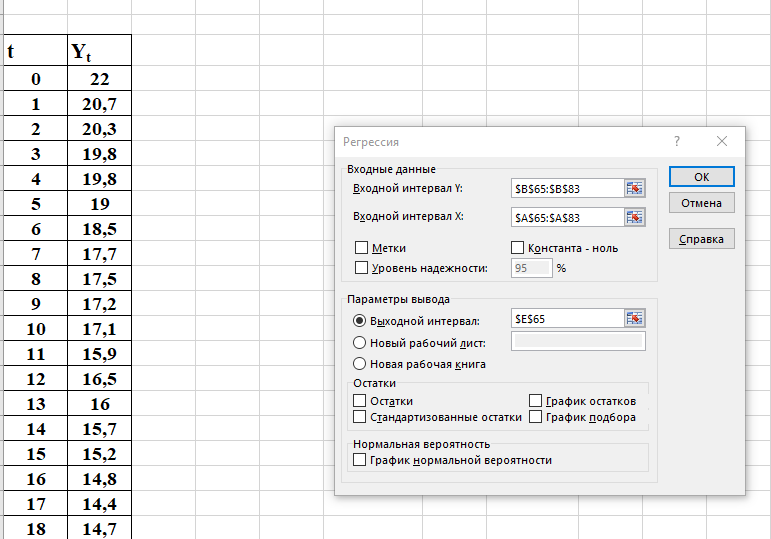 Вывод результатов. 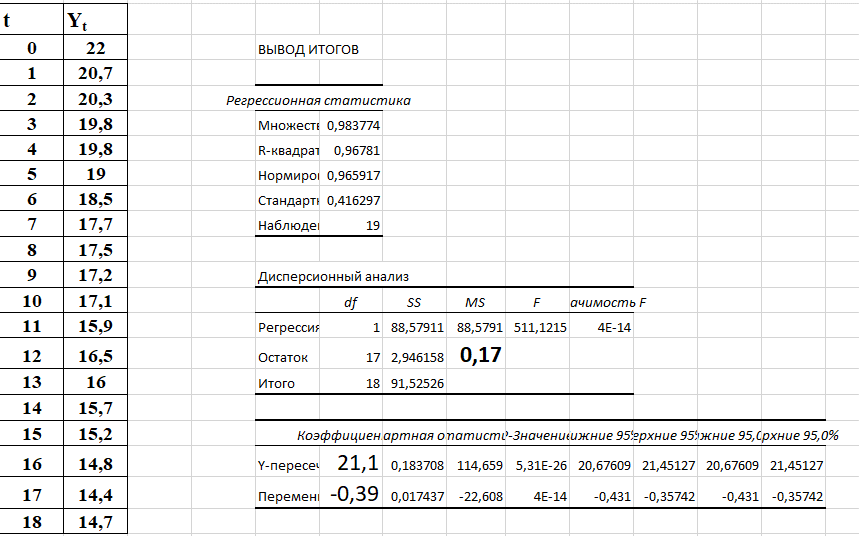 Точечный прогноз на 2018 год: 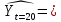 a+b∙t= 21,1 – 0,39×20 = 13,2 (млд.м3). a+b∙t= 21,1 – 0,39×20 = 13,2 (млд.м3).t=21 – номер момента времени, к которому относится прогноз. Интервальный прогноз выполняется с применением формулы, известной из регрессионного анализа. mp = 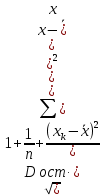 ), где ), где mp - средняя ошибка прогнозируемого индивидуального значения; Остаточная дисперсия Dост = 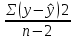 для нашего примера равна 0,17 (выделено жирным шрифтом в таблице ВЫВОД ИТОГОВ для нашего примера равна 0,17 (выделено жирным шрифтом в таблице ВЫВОД ИТОГОВХk= ti = 21 (номер момента времени, к которому относится прогноз). mp = 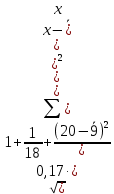 = 0,47 = 0,47Доверительный интервал прогнозируемого значения вычисляется следующим образом. 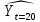 - tα∙ mp < yпр(t=20) < - tα∙ mp < yпр(t=20) <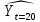 + tα∙ mp + tα∙ mptα – табличное значение критерия Стьюдента для n-2 степеней свободы и уровня значимости α. Для рассматриваемого примера n-2 = 18-2 = 16, α =0,05. 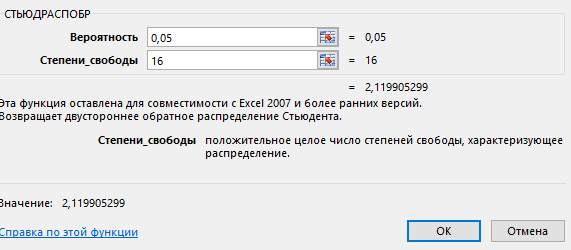 tα = 2,12, следовательно 13,2- 2,12∙ 0,47 < yпр(t=20) <13,2+ 2,12∙ 0,47 Доверительный интервал прогнозируемого значения объема сброса загрязненных сточных вод по бассейнам отдельных рек и морей Российской Федерации (млд.м3) в 2018г следующий : 12,2< yпр(t=20)<14,2 В работах [1], [2], [3] подробно излагаются современные методы анализа информации с применением моделей аддитивного и мультипликативного временных рядов 3.2.3. Анализ аддитивной и мультипликативной моделей временных рядов В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Аддитивная модель имеет вид: Y=T+S+E. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Мультипликативная модель: Y=T×S×E. Основная задача эконометрического исследования отдельного временного ряда – выявление и оценка каждой из перечисленных компонент для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов. Процесс построение аддитивной модели включает в себя следующие шаги: Выравнивание исходного ряда методом скользящей средней. Расчет значений компоненты S. Установление сезонной компоненты из исходных уровней ряда и получение выравненных данных (T+E). Аналитическое выравнивание уровней (T+E) и расчет значений T с использованием полученного уравнения тренда. Расчет полученных по модели значений (T+S). Расчет абсолютных и/или относительных ошибок. Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней: Суммируем уровни ряда последовательно за каждый промежуток времени, в котором наблюдаются колебания со сдвигом на один момент времени и определяем условные величины показателя Y. Делим полученные величины на число моментов времени в промежутке и находим скользящие средние. Находим средние значения из двух последовательных скользящих средних - центрированные скользящие средние. Шаг 2 Оценка сезонной компоненты: Находим оценку сезонной компоненты, как разность между фактическими уровнями ряда и центрированными скользящими средними. Находим средние оценки сезонной компоненты за каждый промежуток времени, в котором наблюдаются колебания S . Из условия взаимопогашения сезонных воздействий определяем корректирующий коэффициент k и рассчитываем скорректированные значения сезонных компонент: в аддитивной модели: Si= S – k Шаг 3 Элиминирование влияния сезонной компоненты: Находим значения Т+Е как Y-S - в аддитивной модели. Шаг 4. Определение трендовой компоненты ряда. Трендовая компонента ряда определяется с помощью построения регрессионной модели, параметры которой находятся методом наименьших квадратов. С помощью уравнения регрессии находим уровни трендовой компоненты Т для каждого момента времени t Шаг 6. Находим значения Т+S Шаг 7. Находим случайную компоненту Е= Y-(T+S) Шаг 8. Оценка качества модели. Находим сумму квадратов случайной компоненты. Находим отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего. Подробно примеры построения обоих типов моделей рассмотрены в [3] Пример построения аддитивной модели потребления электроэнергии за 16 кварталов
Шаг 8. Оценка качества модели. Сумма квадратов абсолютных ошибок: Σ Е2 = 1,679 Отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения: 2,5% Вывод: Построенная аддитивная модель объясняет 97,5% общей вариации уровней временного ряда потребления электроэнергии за 16 кварталов исследуемых 4 – х лет и ее можно использовать в прогнозах будущего потребления электроэнергии. 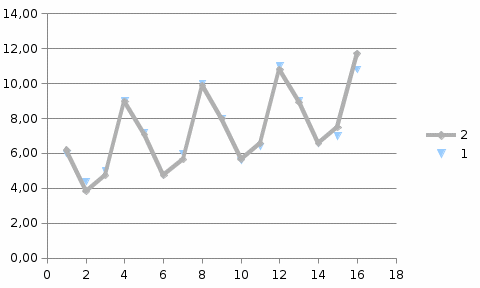 Рис.4. Поквартальное потребление электроэнергии | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
