лаб. Теория вероятностей и математическая статистика (1). Методические указания по их выполнению, а также программа курса и необходимый для решения задач теоретический материал
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
§ 4. Нормальное распределение
О п р е д е л е н и е. Непрерывная случайная величина, имеющая в качестве плотности распределения функцию Функция распределения нормированной нормальной случайной величины, 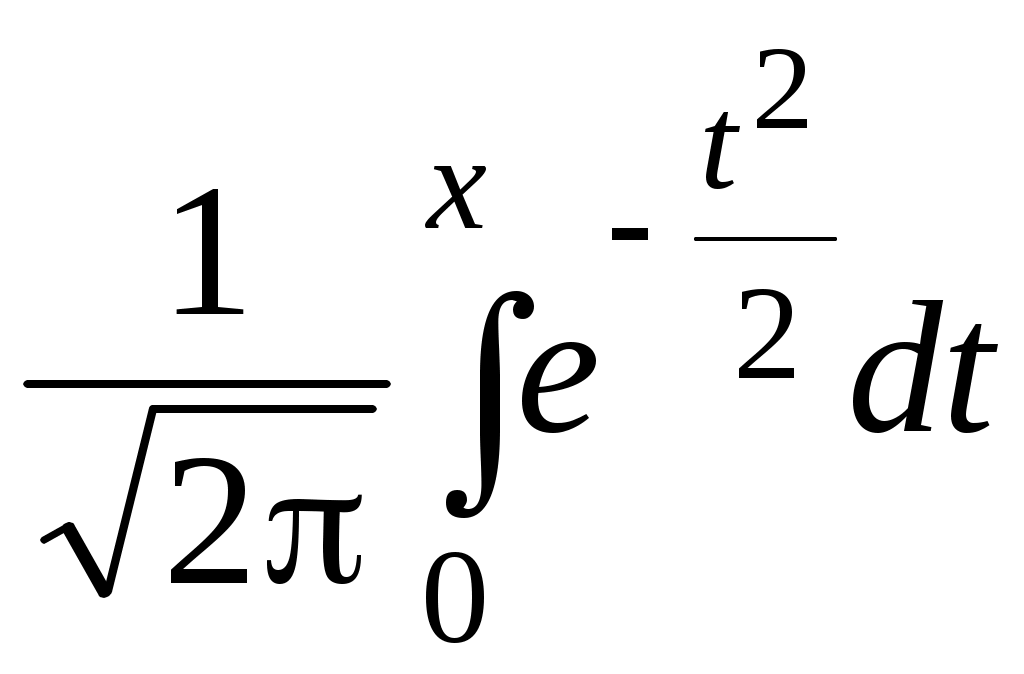 . Этот интеграл является функцией аргумента x, обозначается через φ (x) и называется функцией Лапласа.2 . Этот интеграл является функцией аргумента x, обозначается через φ (x) и называется функцией Лапласа.2 Так как 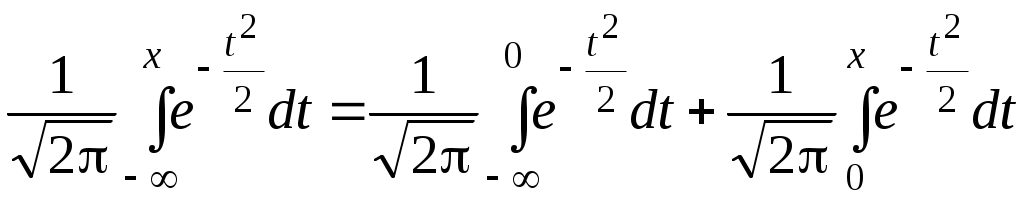 , F(x) = 0,5 + φ (x). , F(x) = 0,5 + φ (x). При помощи функции Лапласа можно найти вероятность попадания нормированной нормальной случайной величины XНН (так мы будем обозначать нормированную нормальную случайную величину)в заданный интервал . 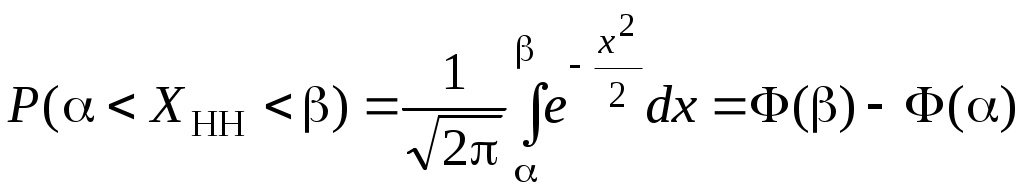 . .Можно показать, что функция Лапласа нечётная, то есть φ (–x)= – φ (x). Ясно также, что φ (+∞) = Вычисления показывают, что математическое ожидание нормированной нормальной случайной величины равно нулю, а среднее квадратическое отклонение – единице. Нормированное нормальное распределение является частным случаем нормального распределения общего вида, которое определяется как распределение непрерывной случайной величины, имеющей в качестве плотности распределения 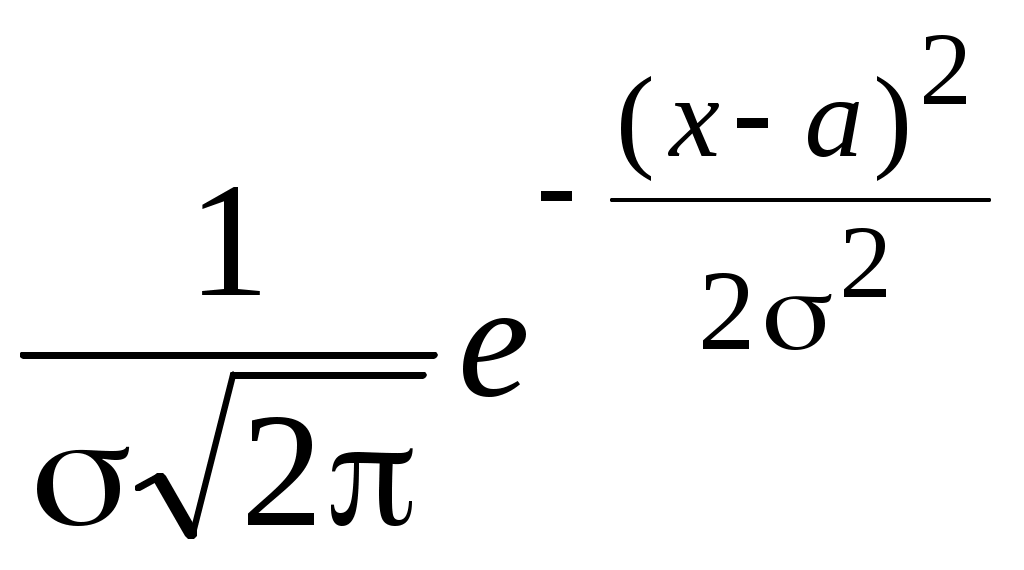 (a и σ – числа, σ > 0). Будем называть такую случайную величину нормальной и обозначать XН. (a и σ – числа, σ > 0). Будем называть такую случайную величину нормальной и обозначать XН.M[XН] = a, σ[XН] = σ. Соответствующие вычисления можно найти в учебниках по теории вероятностей. Выведем формулу для вычисления вероятности попадания нормальной случайной величины в интервал (, ). 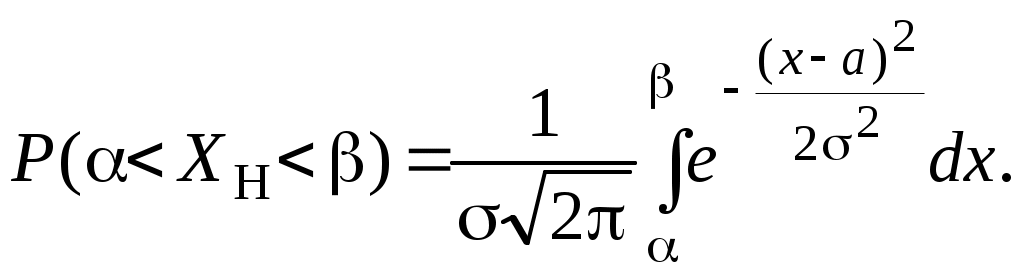 Чтобы вычислить этот интеграл, сделаем замену переменных Чтобы вычислить этот интеграл, сделаем замену переменных 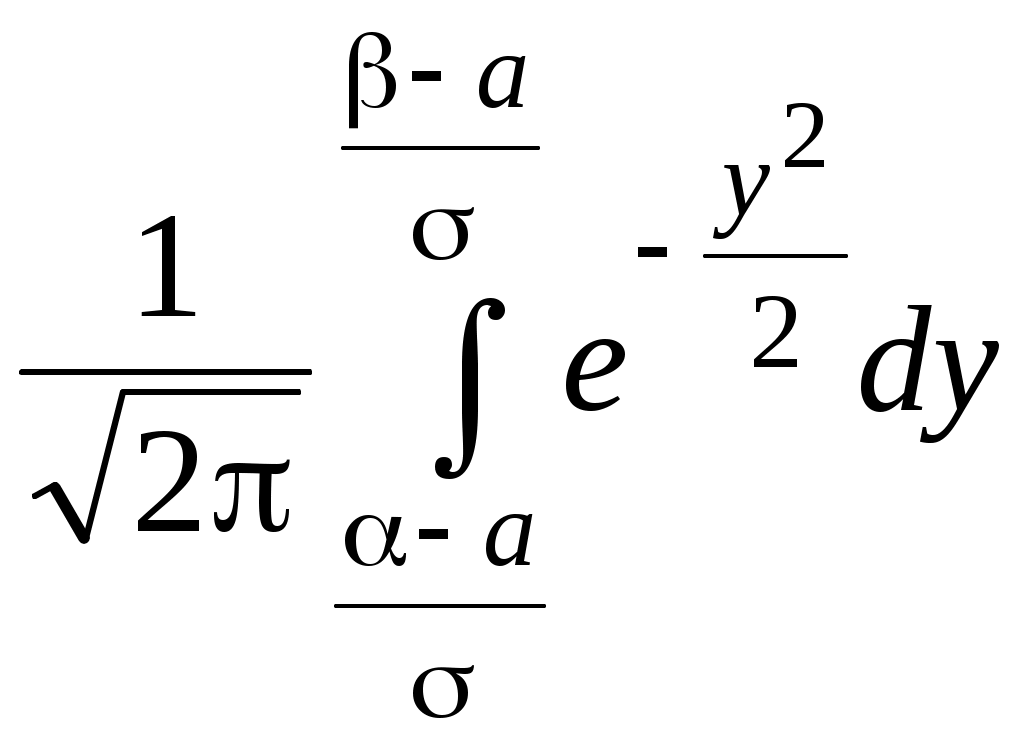 , равный (по формуле Ньютона-Лейбница) разности , равный (по формуле Ньютона-Лейбница) разности Приведём пример применения этой формулы. Полученный результат часто называют правилом «трёх сигма»: вероятность того, что нормальная случайная величина отклонится от своего математического ожидания меньше, чем на три средних квадратических отклонения, практически равна единице.
§ 5. Системы двух дискретных случайных величин Пусть при одном и том же испытании рассматриваются две случайные величины (X, Y) и Y. Тогда каждому элементарному исходу испытания соответствует пара значений (x, y). В этом случае говорят, что задана двумерная случайная величина (X, Y) или, что то же самое, система случайных величин X и Y.
Как и в случае одномерной случайной величины, сум-ма всех вероятностей равна единице, то есть Если вероятности Формулы для вычисления математических ожиданий X и Y приобретают вид: (Если X и Y– компоненты двумерной случайной величины (X, Y), то их математические ожидания обозначаются обычно не Основными числовыми характеристиками двумерной случайной величины (X, Y) являются смешанный момент Смешанный момент определяется равенством Корреляционный момент двумерной случайной величины определяется равенством Дискретные случайные величины X и Y называются независимыми, если P(X= a, Y= b) = P(X= a)P(Y=b). Если X и Y– компоненты двумерной случайной величины (X, Y), условие независимости приобретает вид: Математическое ожидание независимых случайных величин равно произведению математических ожиданий. Действительно, Очевидно, что корреляционный момент независимых случайных величин равен нулю. Коэффициент корреляции определяется равенством Доказано, что коэффициент корреляции обладает свойством Если коэффициент корреляции равен нулю, случайные величины называются некоррелированными. Ясно, что независимые случайные величины являются некоррелированными. Обратное неверно, из некоррелированности независимость не следует. Говорят, что случайные величины X и Y связаны линейной зависимостью, если Y= kX+ b, где kи b – некоторые числа, причём Можно доказать, что если случайные величины X и Y связаны линейной зависимостью, то § 6. Линейное корреляционное уравнение Пусть задана дискретная двумерная случайная величина X и Y. Если коэффициент корреляции по абсолютной величине отличен от единицы, то Yне связан сX линейной зависимостью. Возникает вопрос, при каких значениях коэффициентов kи b случайная величина Для ответа на этот вопрос воспользуемся методом наименьших квадратов, состоящим в том, что наилучшим приближением случайной величины Y считается такое Найдём математическое ожидание квадрата разности Y и M[ ( Напомним, что необходимое условие экстремума функции двух переменных состоит в том, что в точке экстремума частные производные обращаются в 0. В нашей ситуации это означает, что Вычислим частные производные функции 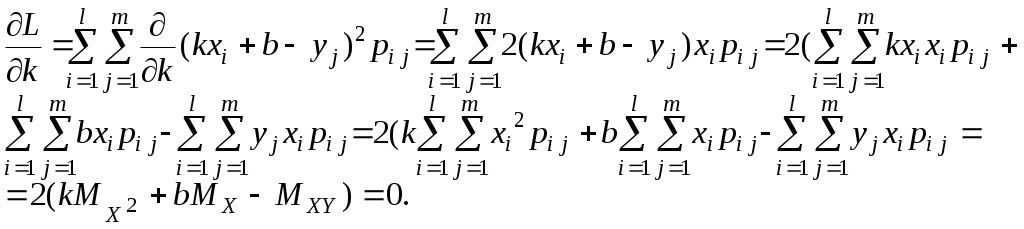 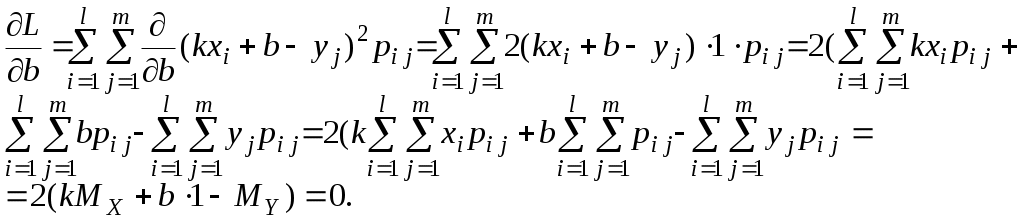 (Пояснение: Получаем систему уравнений 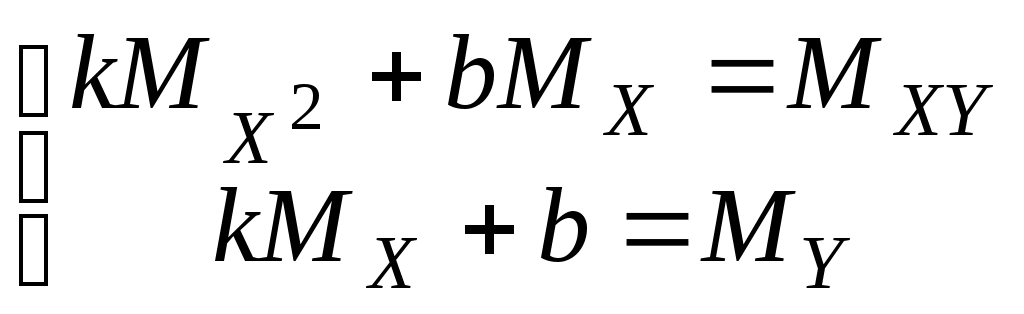 . Главный определитель . Главный определитель Подставим найденные значения kи b в уравнение § 7. Статистический ряд Пусть проведено n испытаний (наблюдений), в результате которых случайная величина приняла n значений, называемых обычно наблюдёнными значениями. Перечень этих значений (среди них могут быть равные) называют выборкой, число n – объёмом выборки. Сама по себе выборка, даже достаточно большого объёма, не даёт представления о характере распределения случайной величины. Чтобы закономерности распределения исследуемой случайной величины проявились, наблюдённые значения случайной величины сводят в интервалы. Как показывает практика обработки статистических данных, величину интервалов следует выбирать так, чтобы их число не более чем на 2-3 единицы отличалось от 12. Пусть Xmaxи Xmin – наибольшее и наименьшее значения выборки. Разделив разность между ними на 12 и округлив результат, получим величину интервала с, то есть В качестве начала первого интервала удобно взять округлённое в меньшую сторону значение Xmin. Число интервалов k должно быть таким, чтобы Xmax, попало в последний, k-й, интервал. Обозначим середины интервалов через
По статистическому ряду строится многоугольник частот – ломаная, соединяющая точки ( |