лаб. Теория вероятностей и математическая статистика (1). Методические указания по их выполнению, а также программа курса и необходимый для решения задач теоретический материал
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
81 – 90. Выравнивание статистического ряда производилось на основании гипотезы о нормальном распределении исследуемой случайной величины. Было найдено Для заданного значения уровня значимости найдите критическое значение 81. k=13, α = 0,01; 82. k =12, α = 0,05; 83. k = 11, α = 0,01; 84.k = 10, α = 0,05; 85.k = 13, α = 0,05; 86.k = 12, α = 0,01; 87.k = 11, α = 0,05; 88.k = 10, α = 0,01; 89.k = 13, α = 0,025; 90.k= 10, α = 0,025; Комментарии к контрольным заданиям 1 – 10. При решении этих задач используются определения и формулы, приведённые в первом параграфе. 11 – 20. При решении задач этой десятки используется формула 21 – 30. Задачи этой десятки решаются по формуле 31 – 40. Нужные для решения задач формулы и чертёж приведены в третьем параграфе. M[ X 2] вычисляется по формуле M[ X 2] = 41 – 50. Математическое ожидание и дисперсия непрерывной случайной величины X вычисляются по формулам, приведённым в третьем параграфе.
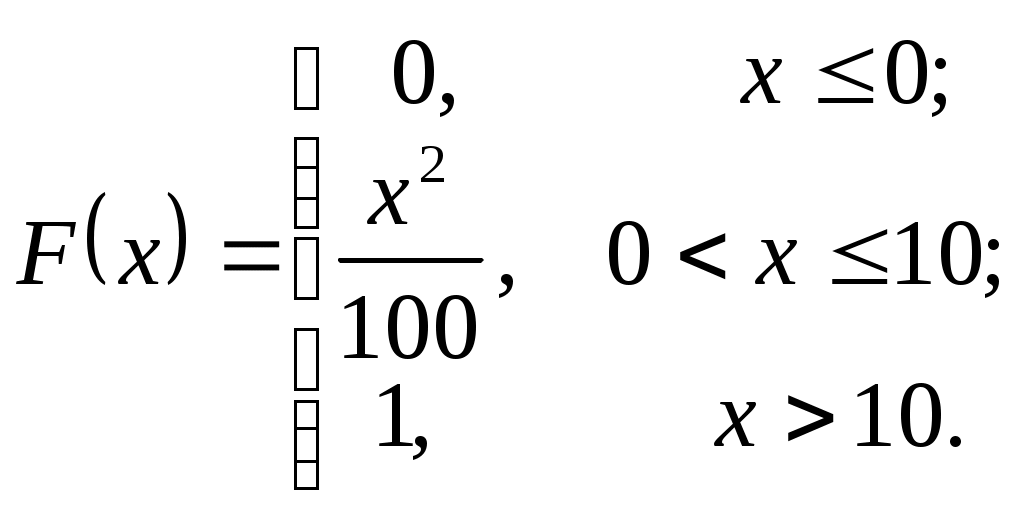 Вычислим плотность распределения: Вычислим плотность распределения: 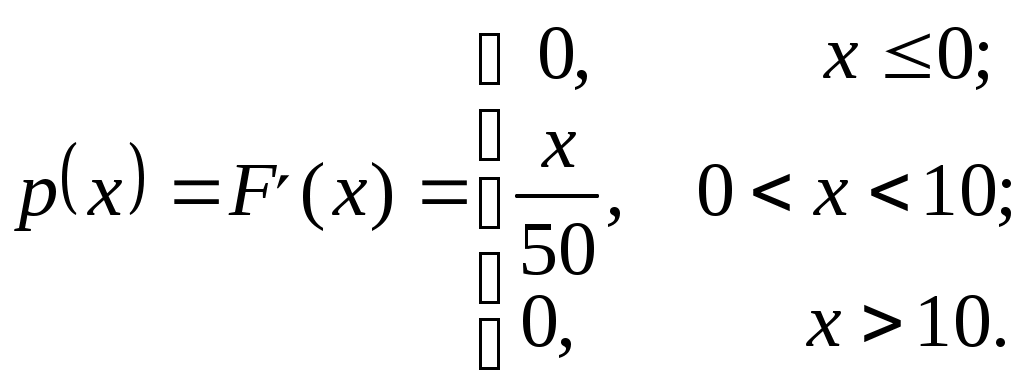 ( (
51 – 60. Вероятность попадания нормально распределённой случайной величины в заданный интервал вычисляется по формуле Приближённые значения функции Лапласа 61 – 70. Пусть двумерная случайная величина (X, Y) задана при помощи таблицы, называемой законом распределения.
Вычислим MX и MY. смешанный момент MXY находим по формуле корреляционный момент Если бы корреляционный момент был отличен от нуля, для вычисления коэффициента корреляции нам пришлось бы найти Аналогично получаем, что Тогда
Получим условный статистический ряд. Найдём условные моменты, затем статистические оценки математического ожидания, дисперсии и среднего квадратического отклонения: 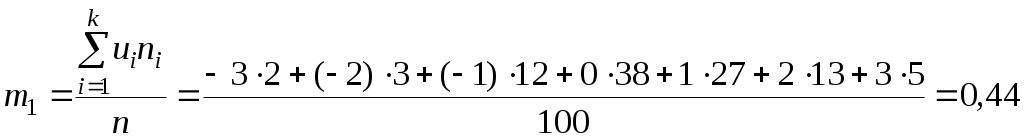 ; ;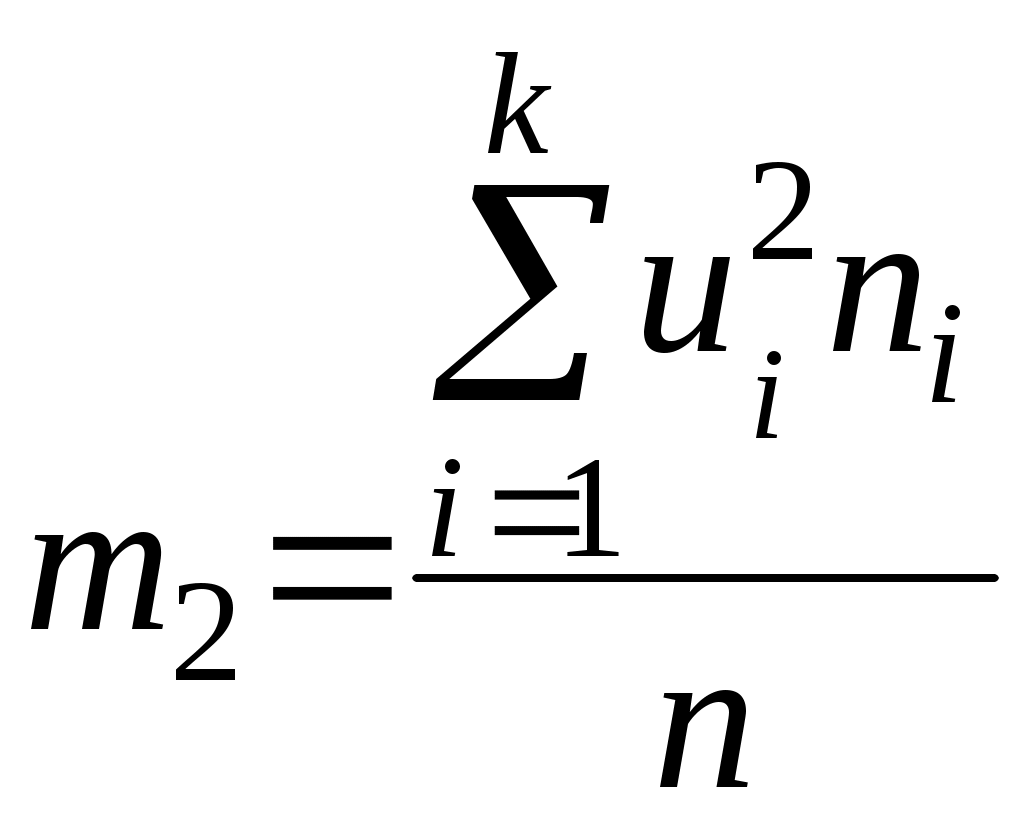 = =Переходим к выравниванию статистического ряда. Выдвигаем гипотезу H: исследуемая случайная величина имеет нормальное распределение с математическим ожиданием 78,52 и средним квадратическим отклонением 9,688. На основании этой гипотезы вычислим выравнивающие частоты. Процесс вычислений оформим в виде таблицы.
Прежде чем вычислять
После объединения число разрядов k стало равным 6. Число степеней свободы определяем по формуле ν = k – 3. Тогда ν = 6 – 3 = 3. В качестве уровня значимости возьмём α = 0,05. По таблице находим критическое значение Поскольку 4,26 < 7,8, то есть
Если была выдвинута гипотеза о нормальном распределении с заранее заданными числовыми значениями a и σ, то ν = k– 1 = 8 – 1 = 7. Тогда Если же в качестве a и σ были взяты, соответственно, Библиографический список Колемаев В. А. Теория вероятностей и математическая статистика. Москва, «Высшая школа», 2000. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. Москва, «Высшая школа», 2001. Гмурман В. Е. Теория вероятностей и математическая статистика. Москва, «Высшая школа», 2003. Вентцель Е. С. Теория вероятностей. Москва, «Наука», 2001. Алексеева В. Е. и др. Элементы математической статистики. Оглавление П р е д и с л о в и е...............................................................................................3 Программа дисциплины «Теория вероятностей и математическая статистика»....................................................................................................................3 Теоретический минимум§ 1. Вероятность случайного события……………………………………..4 § 2. Формула Бернулли. Формула полной вероятности…………………..6 § 3. Случайные величины. Функция распределения и числовые характеристики случайных величин……………………………………….7 § 4. Нормальное распределение…………………………………………….9 § 5. Системы двух дискретных случайных величин……………………..12 § 6. Линейное корреляционное уравнение………………………………..14 § 7. Статистический ряд……………………………………………………15 § 8. Статистические оценки параметров распределения случайной величины……………………………………………………………………16 § 9. Выравнивание статистического ряда………………………………...17 § 10. Распределение § 11. Критерий согласия Пирсона…………………………………………20 Контрольные задания...........................................................................21 Комментарии к контрольным заданиям...................................28Библиографический список..............................................................................33 С о с т а в и т е л ь Алексеева Валентина ЕвгеньевнаТеория ВЕРОятностей и математическая статистика Программа курса, контрольные задания и методические указания для студентов заочного отделения ФЭУ (специальность 080100 экономика) Отпечатано в авторской редакции Компьютерная верстка  Подписано в печать с оригинал-макета Формат 6084/16. Бумага офсетная. Печать трафаретная. Уч.-изд. л. . Печ. л. . Тираж 100 экз. Заказ № . С  Санкт-Петербургская государственная лесотехническая академия Издательско-полиграфический отдел СПбГЛТУ 194021, Санкт-Петербург, Институтский пер., 5 1 Случаи, 2 Функция Иногда функцию Лапласа определяют несколько иначе, например, называют функ-цией Лапласа саму функцию распределения F(x). Поэтому прежде чем пользоваться та-блицами приближённых значений функции Лапласа, нужно посмотреть, какую именно функцию имеют в виду авторы. 3 В этом определении традиционно используются буквы греческого алфавита ξ (кси), χ (хи), ν (ню). 4 Уровнем значимости называется такое число, что события, вероятности которых мень-ше этого числа, считаются практически невозможными. 5 Поскольку контрольная работа по статистике является учебной работой и выполняется по существу вручную, значения функции Лапласа находятся по таблицам, в которых значения аргументов даются с двумя знаками после запятой. Поэтому значения аргументов мы округляем до двух знаков после запятой. Значения функции Лапласа также округляем до двух знаков. При выполнении настоящих научных исследований следует использовать современную вычислительную технику, которая обеспечивает высокую точность. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||