саыв. Мет.указания по выполн.контр.работы. Методические указания по выполнению контрольной работы для слушателей заочной формы обучения
 Скачать 90.33 Kb. Скачать 90.33 Kb.
|
|
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ Оформление контрольных работ осуществляется в соответствии с требованиями ГОСТов. Основные положения по оформлению работ приведены ниже и требуют неукоснительного соблюдения. Контрольная работа является самостоятельной письменной работой, выполняемой студентами в межсессионный период, и ее представление является одним из оснований для вызова студента на экзаменационную сессию. Текст работы печатается на компьютере в текстовом редакторе Word (размер шрифта 14, тип шрифта Times New Roman) через полуторный интервал на одной стороне стандартного листа белой односортной бумаги (А4) без переноса слов по правому краю. Каждый лист должен иметь следующие размеры полей: левое – 30 мм, правое – 12,5 мм, верхнее – 20 мм, нижнее – 20 мм. Выравнивание текста осуществляется по ширине, названия структурных элементов контрольной работы – по центру, отступ в первой строке должен составлять 12,5 мм. Все страницы работы, включая иллюстрации и приложения, нумеруются по порядку от титульного листа до последней страницы посередине верхнего поля арабскими цифрами. Первой страницей считается титульный лист. Все листы нумеруются, начиная со второго листа. Контрольная работа должны содержать следующие структурные элементы: - титульный лист; - содержание; - список используемых сокращений; - введение; - основную часть работы, разбитую на разделы и подразделы; - заключение; - перевод чисел в позиционных системах счисления; - список изученной литературы; - приложения (при необходимости). Основные структурные элементы работы должны начинаться с новой страницы. Титульный лист контрольной работы оформляется в соответствии с приложением № 2. В строке Тема указывается формулировка теоретического вопроса выполняемого варианта контрольной работы. Содержание работы может выполняться с помощью автособираемого оглавления или в виде таблицы без выделения границ. Пример оформления содержания приведен в приложении № 3. Сноски (приложение № 4) выставляются автоматически и имеют постраничную нумерацию, по месту расположения – подстрочные. Выравнивание в сносках осуществляется по ширине с абзацным отступом 12,5 мм. Шрифт сносок Times New Roman, кегль 10, межстрочный интервал – 1 пт, запрет автоматических переносов слов. Список литературы (приложение № 5) должен включать изученную и использованную в работе литературу. На каждый источник, указанный в списке литературы, в тексте работы должна быть дана ссылка. Работа представляется в сброшюрованном виде в папке со скоросшивателем или в папке с файлами. Объем теоретической части контрольной работы определяется разумной необходимостью и должен быть в пределах 8…12 листов машинописного текста. Практическая часть работы оформляется после заключения по теоретическому вопросу под заголовком Перевод чисел в позиционных системах счисления. Она должна содержать не только результат перевода числа из одной системы счисления в другую, но и последовательность решения, согласно используемой методики. Объем данной части работы зависит от выбранной формы представления информации. Приложение 1 Методика перевода чисел в позиционных системах счисления В позиционных системах счисления значение цифры в записи числа зависит от того, какую позицию (разряд) в числе оно занимает. Например, в записи десятичного числа 101 цифра один, стоящая в третьем (старшем) разряде означает одну сотню, а стоящая в первом (младшем) разряде – одну единицу. Количество цифр, используемых для записи чисел в конкретной системе счисления, называется основанием системы. В двоичной системе счисления для записи чисел используется только две цифры 0 и 1, в восьмеричной – восемь цифр от 0 до 7, в десятичной – десять от 0 до 9. В шестнадцатеричной системе счисления для записи чисел используется 16 символов: десять цифр от 0 до 9 и шесть первых букв латинского алфавита A, B, C, D, E, F. Следовательно, при переводе шестнадцатеричных чисел в другие системы счисления и обратно необходимо помнить о соответствии букв следующим значения десятичной системы:
Правило перевода из десятичной в любую систему счисления. Для перевода целой части: - целую часть десятичного числа последовательноделить на основание системы, в которую выполняется перевод. Деление выполнять пока результат деления не станет меньше основания системы. - к результату последнего деления дописать полученные при делении остатки, в порядке, обратном их получению. Для перевода дробной части: - дробную часть десятичного числа последовательно умножать на основание системы, в которую выполняется перевод, отделяя целую часть. Умножение продолжать, пока дробная часть не станет равной 0 или не будет достигнута требуемая точность (обычно 3-4 знака); - записать целые части результатов умножения в порядке их получения. Пример 1. Перевести 26,25 из десятичной в двоичную систему счисления. 26,2510 → ?2 Решение: перевод целой части числа: перевод дробной части числа: 0, 25 * 2 0 50 * 2 1 00 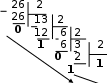 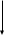 Ответ: 26,2510→11010,012 П 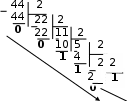 ример2. Перевести 44,75 в двоичную систему счисления. ример2. Перевести 44,75 в двоичную систему счисления.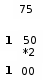 *2 Другой способ записи перевода числа (более удобный для оформления на ПК в текстовом редакторе): 44 : 2 = 22, остаток 0 0,75 * 2 = 1, 50 целая часть 1 22 : 2 = 11, остаток 0 дробная часть 0,5 11 : 2 = 5, остаток 1 0, 5 * 2 = 1,0 целая часть 1 5 : 2 = 2, остаток 1 дробная часть 0 2 : 2 = 1, остаток 0 Ответ: 44,7510→101100,112 Пример 3. Перевести 376,75 из десятичной в восьмеричную систему счисления. 376 : 8 = 47, остаток 0 0,75 * 8 = 6, 00 целая часть 6 47 : 8 = 5, остаток 7 дробная часть 0 Ответ: 376,7510→570,68 Пример 4. Перевести 590,765625 из десятичной в шестнадцатеричную систему счисления. 590 : 16 = 36, остаток 14 0,765625 * 16 =12,25, целая часть 12 36 : 16 = 2, остаток 4 дробная часть 0,25 0, 25 * 16 = 4,00, целая часть 4 дробная часть 0 При записи целой части вместо 14 записывается Е, при записи дробной части вместо 12 записывается С! Ответ: 590,76526510→24Е,С416 Правило перевода в десятичную систему счисления. В позиционной системе счисления с основанием Q любое число х может быть представлено в виде полинома: x   = аnQn +……+ a2Q2 + a1Q1 + a0Q0 + a–1Q –1 + a–2Q –2 + a–m Q-m = аnQn +……+ a2Q2 + a1Q1 + a0Q0 + a–1Q –1 + a–2Q –2 + a–m Q-mцелая часть дробная часть где а – значение разряда числа; Q – основание системы счисления исходного числа, т.е. 2, 8 или 16. Правило перевода можно сформулировать следующим образом. Для перевода числа в десятичное необходимо представить число в виде суммы произведений цифр числа на степень основания его системы счисления, соответствующей позиции цифры в числе (разряду). Алгоритм перевода, соответствующий данному правилу: записать над каждой цифрой его позицию в числе: в целой части - влево от запятой положительными числами, начиная с нуля; в дробной части - вправо от запятой отрицательными числами, начиная с минус единицы. Это и будут показатели степеней, в которые возводится основание исходной системы счисления при переводе; записать выражение в виде полинома, т.е. суммы произведений каждой цифры числа на основание исходной системы счисления в степени, соответствующей позиции цифры в числе; произвести вычисление выражения в десятичной системе счисления. Пример 5. Перевести число 11010,012 в десятичную систему счисления. 4 3 2 1 0 -1 -2 показатели степеней основания системы 11010,012 → 1∙24 + 1∙23 + 0∙22 + 1∙21 + 0∙20 + 0∙2-1 + 1∙2-2 = 1∙16 + 1∙8 + 0∙4 + 1∙2 + 0∙1 + 0∙1/2 + 1∙1/22 =16+8+0+2+0+0+0,25=26,25 Ответ: 11010,012 → 26,25 Пример 6. Перевести восьмеричное число 703,048 в десятичную систему счисления. 2 1 0 -1 -2 показатели степеней основания системы 703,048 → 7∙82 + 0∙81 + 3∙80 + 0∙1/8 + 4∙1/82 =7∙64 + 0∙8 + 3∙1+0∙0,125+4/64= 448+0+3+0+0,0625=451,0625 Ответ: 703,048 → 451,062510 Пример 7. Перевести число В2Е,4 в десятичную систему счисления. 2 1 0 -1 - показатели степеней основания системы В2Е,416 → 11∙162 + 2∙161 + 14∙160 + 4∙1/16 =11∙256 + 2∙16 + 14∙1+4/16= 2816+32+14+0,25=2862,2510 Ответ: В2Е,416 → 2862,2510 Цифры восьмеричной и шестнадцатеричной систем счисления имеют однозначное соответствие цифрам двоичной системы, т.к. 8=23, а 16= 24. Поэтому каждая цифра восьмеричной системы счисления представляется двоичным числом из трех разрядов, а шестнадцатеричной – из четырех разрядов. Таблица перевода чисел
Чтобы не заучивать данную таблицу, при переводе цифр можно использовать следующий алгоритм. При переводе восьмеричной цифры в двоичное число и обратно записать последовательно степени двойки. 22 21 20. 4 2 1. Цифра 5 получается сложением цифр нулевого и второго разрядов, следовательно в данных разрядах записать 1, а в первом – 0. 1 0 1 Результат: 58 → 101. При обратном переводе, например числа 1102 в восьмеричную цифру, сложить цифры в разрядах, соответствующих единицам, т.е. 4+2=6. Результат: 1012→ 6. При переводе цифры шестнадцатеричного числа в двоичное число и обратно записать четыре степени двойки. 23 22 21 20. 8 4 2 1. Символ D соответствует числу 13. Оно «набирается» суммой третьего, второго и нулевого разрядов. Пишем 1 1 0 1. Результат: D → 1101. Число 0100 содержит 1 только во втором разряде, в котором стоит число 4, значит 0100 → 416. Правило перевода из восьмеричной и шестнадцатеричной систем счисления в двоичную. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления. Алгоритм перевода, соответствующий данному правилу: Каждую цифру рассматривать как отдельное число. Перевести каждую цифру в двоичную систему счисления в эквиваленте исходной системы счисления. Последовательно записать полученные двоичные числа группами из трех разрядов при переводе из восьмеричной системы счисления, из четырех разрядов – при переводе из шестнадцатеричной системы счисления. Нули перед целой частью и в конце дробной являются незначащими, поэтому отбрасываются при записи результата. |
