экономическая статистика. Методические указания по выполнению контрольной работы по дисциплине статистика
 Скачать 238 Kb. Скачать 238 Kb.
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «СТАТИСТИКА» Введение Статистика является общественной наукой, которая изучает явления и процессы общественной жизни в их количественно-качественной определенности. Она разрабатывает общие положения и методы статистического исследования. Ее категориями, показателями и методами пользуются все другие отрасли статистической науки. В результате изучения студенты овладевают знаниями общих основ статистической науки и общими навыками проведения статистического исследования, изучают методология сбора, обработки и анализа статистической информации. В соответствии с учебным планом студенты заочной формы обучения специальностей «Государственное и муниципальное управление», «Связи с общественностью», «Реклама» и «Политология» выполняют контрольную работу по курсу статистика. Цель контрольной работы – изучить важнейшие методологические вопросы, проверить умение студента применять на практике основные положения курса, приобрести практические навыки в расчетах статистических показателей, научить понимать экономический смысл исчисленных показателей, анализировать их и изображать графически. 1. Требования по оформлению контрольной работы и РГР Выполненная контрольная работа должна соответствовать следующим требованиям: − работа должна быть выполнена и представлена на рецензирование в срок, установленный преподавателем; − задачи следует решать в том порядке, в каком они даны в задании; − перед решением задачи должно быть полностью приведено ее условие; − решение задач следует сопровождать необходимыми формулами, подробными расчетами и краткими пояснениями, изображать графически. Произведенные расчеты нужно проверять взаимосвязью между исчисленными показателями. Необходимо четко формулировать выводы, раскрывающие экономическое содержание и значение исчисленных показателей. Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты до 0,1. Студенты, не получившие зачета по контрольной работе к зачету/экзамену не допускаются. Если выполнение контрольной работы и вызывает затруднения, следует обратиться за консультацией. 2. Указания о порядке выполнения контрольной работы и ее содержание Приступить к выполнению контрольной работы следует после проработки теоретического материала. Контрольная работа по статистике состоит из шести вариантов, в каждом варианте соответственно по 8 задач. Выбор варианта определяется последней цифрой зачетной книжки студента (таблица 1): Таблица 1
Общая теория статистики Задача 1 составлена на тему «Абсолютные и относительные величины». Существуют следующие виды относительных величин: − выполнение договорных обязательств (задания, плана) показывает отношение фактических показателей к договорным или плановым; − структуры, показывают отношение частей к целому или отношение групп ко всей совокупности; − динамики или темпы роста, показывают изменение явления во времени, характеризуют рост или снижение каких-либо показателей в сравниваемых периодах. При расчёте темпов роста различают два периода: базисный и отчётный. Относительная величина динамики (темп роста, базисный) – это отношение уровня показателя каждого периода к первоначальному уровню с постоянной базой сравнения. Относительная величина динамики (темп роста, цепной) – это отношение уровня показателя каждого периода к первоначальному уровню с переменной базой сравнения. − сравнения, сопоставляются уровни одноименных показателей относящиеся к различным объектам наблюдения, взятым за один пи тот же период времени или на один момент времени; − координации, представляют собой одну из разновидностей показателей сравнения; − интенсивности, характеризуют степень распространенности или развития того или иного влияния в определенной среде. Чаще всего они 5 выражаются в именованных величинах. Задачи 2 и 3 составлены по темам «Средние величины» и «Показатели вариации». Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средние, используемые в статистике, относятся к двум классам: степенные средние и структурные средние. Из первого класса наиболее часто применяются средняя арифметическая и средняя гармоническая. Средняя геометрическая применяется только при исчислении средних показателей рядов динамики, средняя квадратическая – при исчислении показателей вариации. Представителями второго класса средних являются мода и медиана. Если данные таковы, что в исходном соотношении средней не известен числитель, а известен знаменатель, то данное соотношение приводит к исчислению средней арифметической взвешенной: 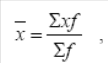 где x – варианты признака; f – частоты. Если данные таковы, что в исходном соотношении средней известен числитель, а не известен знаменатель, то данное соотношение приводит к исчислению средней гармонической взвешенной: 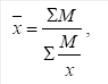 где М – суммарный объем признака в данной группе. Исследование вариации является составным элементом статистического анализа, позволяющим оценить колебания значений изучаемого признака, однородность совокупности по данному признаку, взаимосвязь его с другими признаками. Показатели вариации служат критерием типичности рассчитанных по совокупности средних величин, используются в определении ошибок выборочных характеристик. При изучении данной темы необходимо обратить особое внимание на расчет основных показателей вариации: Размах вариации (R): R= xmax – xmin, где xmax, xmin – максимальное и минимальное значение признака соответствено. Среднее линейное отклонение (d):  – для сгруппированные данных, – для сгруппированные данных,  – для несгруппированных данных, – для несгруппированных данных,где n – число вариант Дисперсия (σ2): Среднее квадратическое отклонение (σ): Коэффициент вариации: Задача 4 составлена по теме «Ряды динамики». Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для ее отражения строятся ряды динамики. Ознакомившись с литературой и рассмотрев ряды динамики, опубликованные в статистических ежегодниках и справочниках студент должен уяснить, что такое ряд динамики и как он строиться. Особое внимание следует обратить на условия сопоставимости данных, составляющих динамический ряд. При рассмотрении вопросов о видах рядов динамики надо, прежде всего, понять различие между моментными и интервальными рядами. Построение, обработка и анализ этих рядов во многом определяется их особенностями. Затем следует перейти к изучению методов расчета аналитических показателей рядов динамики. Рассчитывая аналитические показатели ряда динамики, необходимо правильно выбирать базу для сравнения. Этому вопросу следует уделить особое внимание. Необходимо также разобраться в способах получения средних величин ряда: среднего уровня, среднего абсолютного прироста, среднего темпа роста и прироста. Следует помнить, что способ расчета среднего уровня ряда динамики зависит от его вида. При расчете среднего темпа роста необходимо использовать среднюю геометрическую. Важнейшие статистические показатели: − абсолютный прирост (цепной) Δy=yi-yi-1; − абсолютный прирост (базисный) Δy=yi-y0, где yi- уровень сравниваемого периода; yi-1 – уровень предшествующего периода; y0 – уровень базисного периода; − темп роста (цепной) − темп роста (базисный) − темп прироста Тпр=Тр-100; − абсолютное значение одного процента прироста Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики при равных интервалов применяется средняя арифметическая простая:  , ,где y – абсолютные уровни ряда; n – число уровней ряда при неравных интервалах – средняя арифметическая взвешенная:  где y1, …, yn – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t; t1, …, tn – веса, длительность интервалов времени между смежными датами. Средний уровень для моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:  , ,где y1,…, yn – уровни периода, за который делается расчет; n – число уровней периода; n-1 – длительность периода времени Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной: 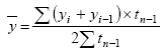 где yI, yn – уровни рядов динамики; t – интервал времени между смежными уровнями. Средний абсолютный прирост (убыль): цепным способом расчета: где n – число цепных абсолютных приростов (Δyц) в изучаемом периоде базисным способом расчета: где m – число уровней ряда динамики в изучаемом периоде, включая базисный Средний темп роста: − по цепному способу расчета где n – число цепных коэффициентов роста; Кцр1,…, Кцрn – цепные коэффициенты роста. − по базисному способу расчета где m – число уровней ряда динамики в изучаемом периоде, включая базисной. Средний темп прироста: Задачи 5 и 6 составлены по теме «Индексы». Индексы могут быть индивидуальными и сводными. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. Сводные индексы отражают изменение всех элементов сложного явления. Под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию. Сводный индекс цен может исчисляться в агрегатной, среднеарифметической или среднегармонической формах. Например, для индекса цен: агрегатный  средний арифметический 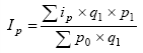 средний гармонический  , ,где р – цена; q – количество товаров; Ip – индивидуальный индекс цен. При решении задач следует ясно представлять взаимосвязь индексов в формуле: отсюда: Эта взаимосвязь сохраняется между индексами, исчисленными по любым формулам. Взаимосвязь индексов позволяет исчислить изменение стоимости за счёт изменения цены и физического объёма реализации в абсолютном выражении: в том числе:  Для проверки правильности расчётов можно использовать равенство: Особое внимание необходимо уделить индексному методу изучения динамики среднего уровня. На изменения среднего значения показателя оказывают воздействие два фактора (изменение значения индексируемого показателя у отдельных групп единиц и изменение структуры явления), возникает задача определить степень влияния каждого из факторов на общую динамику средней. Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включается три индекса: переменного состава, постоянного состава и структурных сдвигов. Индекс переменного состава: 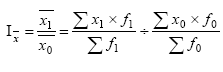 где х1 и х0 – уровни осредняемого показателя в отчетном и базисном периодах соотвественно; f1 и f0 – веса (частоты) осредняемого показателя в отчетном и базисном периодах соотвественно; Индекс постоянного (фиксированного) состава: 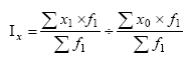 Индекс структурных сдвигов: 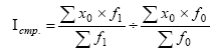 Взаимосвязь: Задача 7 составлена по теме ″Статистическое изучение взаимосвязи социально-экономических явлений″. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой). Таблица для вычисления коэффициентов ассоциации и контингенции: 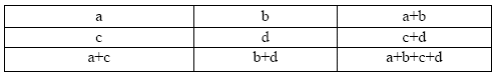 Коэффициенты определяются по формулам: ассоциации контингенции Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденный, если Ка≥0,5 или Кк≥0,3. Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона и Чупрова: 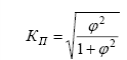  где ϕ2 – показатель взаимной сопряженности; ϕ – определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы 1, получим величину ϕ2. К1 – число значений (групп) первого признака; К2 - число значений (групп) второго признака. Чем ближе величины КЧ и КП к 1, тем связь теснее. Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Коэффициент корреляции рангов Спирмена рассчитывается по формуле: 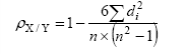 где di2 – квадрат разности рангов; n – число наблюдений (число пар рангов). Задача 8 может обноситься к любой теме социально-экономической статистике по нескольким типам. Задача тип а составлена по теме «Статистика населения». Население как объект изучения статистики представляет собой совокупность людей, проживающих на определённой территории и непрерывно возобновляющихся за счёт рождения и смертей. Абсолютные показатели естественного движения населения: число родившихся (N), число умерших (М), абсолютный естественный приростΔ Относительные показатели естественного движения населения: 1) общий коэффициент рождаемости: 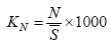 , ,где S – среднегодовая численность населения 2) общий коэффициент смертности: 3) коэффициент естественного прироста населения: 4) специальный коэффициент рождаемости:  где 5) коэффициент детской (младенческой) смертности: 6) показатель жизненности населения: Абсолютные показатели механического движения: число прибывших (П), число выбывших (В), абсолютный механический прирост Относительные показатели механического движения: 1) коэффициент прибытия: 2) коэффициент выбытия: 3) коэффициент механического прироста Для определения изменения численности населения как за счёт рождаемости и смертности, так и за счёт миграции исчисляются коэффициент общего прироста населения:  где Sн.г. и Sк.г. – численность населения соответственно на конец и на начало года Перспективная численность населения через t лет:  где SH – численность населения на начало планируемого периода; t – число лет, на которое прогнозируется расчет; Кобщ.пр. – коэффициент общего прироста населения за период, предшествующий плановому. Задача тип б составлена по теме «Статистика трудовых ресурсов». Трудовые ресурсы – население, занятое экономической деятельностью или способное трудиться, но не работающее по тем или иным причинам. В состав трудовых ресурсов включается: население в трудоспособном возрасте (мужчины 16 – 59 лет и женщины 16 – 54), кроме неработающих инвалидов 1 и 2 групп и неработающих лиц, получающих пенсию на льготных условиях; работающие подростки и работающие лица пенсионного возраста. Экономически активное население (рабочая сила) – часть населения, которая предлагает свой труд для производства товаров и услуг. Численность экономически активного населения включает занятых и безработных. К занятым в экономике относятся лица обоего пола в возрасте 16 лет и старше, а также младших возрастов, которые в рассматриваемый период выполняли работу по найму за вознаграждения, а также приносящую доход работу не по найму самостоятельно или с одним или несколькими партнерами как с привлечением, так и без привлечения наемных работников. Уровень безработицы определяется отношением общей численности безработных к численности экономически активного населения. Задача тип в по теме «Статистика основных фондов». Основные фонды – это произведённые активы, подлежащие использованию неоднократно в течение длительного периода времени для производства товаров. Различают следующие виды стоимостной оценки основных фондов: 1) полная первоначальная стоимость (ППС) – это стоимость объекта на момент ввода его в эксплуатацию 2) остаточная первоначальная стоимость – это ППС за вычётом суммы износа основных фондов за время их эксплуатации 3) полная восстановительная стоимость (ПВС) – это стоимость воспроизводства основных фондов в современных условиях 4) остаточная восстановительная стоимость – это ПВС основных фондов за вычетом суммы износа 5) балансовая стоимость – это стоимость объектов с учётом переоценки, по которой они числятся на балансе предприятия Баланс основных фондов по полной балансовой стоимости: ПС к.г. =ПС н.г. + П – В, где ПСк.г., ПСн.г. – наличие основных фондов соответственно на начало и конец года; П – стоимость основных фондов, поступивших в течение года; В – стоимость выбывших основных фондов в течение года. Баланс основных фондов по остаточной балансовой стоимости: ОС к.г.= ОС н.г.+ П – В ос+ КР – А, где ОС к.г. и ОС н.г. – наличие основных фондов на начало конец года за вычетом износа; Вос – стоимость выбывших основных фондов за вычетом износа; КР – стоимость капремонта; А – сумма амортизации. 1. Показатели состояния основных фондов: Коэффициент износа на начало и конец года: Кизноса н.г.=Ин.г./ПСн.г.=(ПСн.г.-Осн.г.)/ПСн.г.*100% где Ин.г. – сумма износа на начало года Кизноса к.г.=Ик.г./ПСк.г.=(ПСк.г.-Оск.г.)/ПСк.г.*100% Коэффициент годности: Кгод. = 1 – Кизноса Кгод. = Осн.г. или Оск.г./ПСн.г. или ПСк.г.*100% 2. Показатели движения основных фондов: Коэффициент обновления: Кобн = П/ПСк.г. * 100% Коэффициент выбытия: Квыб = В/ПСн.г. * 100% Денежное выражение физического и морального износа основных фондов называется амортизацией. Годовая норма амортизации рассчитывается как отношение годовой суммы амортизационных отчислений (А) к среднегодовой стоимости основных фондов (ОФ): 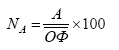 Задачи тип г по теме «Система национальных счетов» посвящены методам исчисления валового внутреннего продукта (ВВП): 1) производственный метод: ВВП= ВДС+ЧНП, где ВДС – суммарная величина валовой добавленной стоимости за вычетом косвенно измеряемых услуг финансового посредничества: ВДС = В – ПП, где В – выпуск товаров и услуг; ПП – промежуточное потребление; ЧНП – чистые налоги на продукты 2) распределительный метод: ВВП = ОТ + ЧНПИ + ВП + ВСД, где ОТ – оплата труда наёмных работников; ЧНПИ – чистые налоги на производство и импорт; ВП – валовая прибыль; ВСД – валовые смешанные доходы. 3) метод конечного использования: ВВП = КП + ВН + С, где КП – конечное потребление; ВН – валовое накопление; С – сальдо экспорта и импорта товаров и услуг. Индекс-дефлятор ВВП (Ιдеф.ВВП) рассматривается как показатель, наилучшим образом отражающий динамику общего уровня цен:  , ,где ВВП1 = Σp1 × q1 – объем ВВП текущего периода в фактических ценах; ВВП'1 = Σp0 × q1 – объем ВВП текущего периода в постоянных ценах. Задача тип д по теме «Статистика доходов населения». Показатели номинальных доходов всегда характеризуют сумму начисленных доходов. За вычетом налогов и обязательных платежей номинальные доходы населения образуют располагаемые доходы, т.е. доходы, фактически остающиеся в распоряжении населения. Поэтому их можно считать конечными доходами. Реальные доходы населения за период определяются соотношением его конечных доходов за этот период и индекса потребительских цен. Средняя номинальная заработная плата рассчитывается по начисленному фонду оплаты труда и соответствующей численности работников. Средняя реальная заработная плата определяется исходя из средней номинальной за вычетом налогов и обязательных платежей, деленной на индекс потребительских цен на товары и услуги. Индекс покупательной способности рубля: 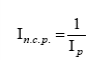 , ,где 3 Контрольная работа по общей теории статистике Вариант 4 Задача 1 Имеются условные данные о показателях деятельности промышленной фирмы:
Исчислите все возможные виды относительных величин. Задача 2 Имеются данные о продаже акций компании «А» на торгах фондовой биржи:
Исчислите средний курс реализации акций, используя формулы средней арифметической и средней гармонической. Задача 3 В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена 10%-ная механическая выборка, в результате которой получено следующее распределение изделий по массе:
Определите: 1) средний вес изделия; 2) коэффициент вариации. Объясните смысл полученного значения коэффициента вариации. Задача 4 Имеются следующие условные данные о производстве отдельных видов продукции пищевой промышленности РФ; (тыс. т):
1. Исчислить следующие показатели динамики: а) абсолютный прирост (на цепной и базисной основе); б) темп роста и прироста (на цепной и базисной основе); в) абсолютное значение 1% прироста; г) средний уровень ряда динамики; д) средний абсолютный прирост, средний темп роста и прироста. 2. Показать взаимосвязь между исчисленными базисными и цепными показателями динамики. 3. Изобразить интенсивность развития ряда динамики графически. Задача 5 Имеется следующая информация о реализации овощей и ценах на рынках города:
На основе приведенных данных определите: 1) индивидуальные индексы цен и физического объема; 2) общий индекс физического объема; 3) общий индекс цен; 4) сумму экономического эффекта от продажи данных продуктов в отчетном периоде по измененным ценам. Задача 6 Имеются следующие данные о продаже продукта В на рынках города:
На основе приведенных данных определите: 1) индекс цен постоянного состава; 2) индекс цен переменного состава; 3) индекс структурных сдвигов; 4) изменение средней цены (в абсолютных величинах) в январе по рынкам города в целом и за счет действия отдельных факторов. Сделайте выводы. Задача 7 Имеются следующие данные по 9 предприятиям об объеме реализованной продукции и балансовой прибыли:
Рассчитайте коэффициент корреляции рангов Спирмена. Объясните экономический смысл рассчитанного показателя и сделайте выводы. Задача 8. Имеются данные о результатах экономической деятельности РФ млрд. р.:
Определите валовой внутренний продукт(ВВП): а) производственным методом; б) распределительным методом; в) методом конечного использования. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
