му. МУ к КР по ТЭЦ-издано (1). Методические указания по выполнению курсовой работы по дисциплине Теория электрических цепей

• Название: Методические указания по выполнению курсовой работы по дисциплине Теория электрических цепей
• Дата: 04.02.2022
• Размер: 1.88 Mb.
• Имя файла: МУ к КР по ТЭЦ-издано (1).doc
• Тип: Методические указания; #351447
• страница: 2 из 4

Определяются искомые токи в цепи путём суммирования свободных и установившихся их составляющих.

7) Определяется переходная характеристика по напряжению заданного четырёхполюсника, считая внешним воздействием на цепь – напряжение на входных зажимах, а реакцией цепи – напряжение на выходных зажимах четырёхполюсника. Переходная характеристика по напряжению линейного четырёхполюсника, не содержащего независимых источников напряжения, численно равна выходному напряжению четырёхполюсника при его подключении в момент времени t=0 к источнику единичного напряжения.

2.2.2 Пример расчёта



Рисунок 2.2.1. Эквивалентная схема четырёхполюсника
Производим расчёт цепи до коммутации. До коммутации токи во всех ветвях электрической цепи и напряжения на всех элементах равны нулю:
(2.2.6)
Используя законы коммутации, находим независимые начальные условия, представляющие собой ток индуктивности и напряжение ёмкости в момент времени (t=0).
(2.2.7)
Составим систему дифференциальных уравнений, описывающую процесс в цепи после коммутации (t>0):



Рисунок 2.2.2. Эквивалентная схема четырёхполюсника после коммутации

Выбираем произвольно направление обхода контура
(2.2.8)
Искомые токи представим в виде суммы установившегося и свободного режима цепи:
(2.2.9)

где - установившаяся составляющая первого тока;

- установившаяся составляющая второго тока;

- установившаяся составляющая третьего тока;

- свободная составляющая первого тока;

- свободная составляющая второго тока;

- свободная составляющая третьего тока.
Определим частное решение системы неоднородных дифференциальных уравнений, то есть токи и напряжения установившегося режима. Так как на входе цепи включена ёмкость, то значения установившихся токов будут равны нулю.

(2.2.10)
Определим общее решение системы однородных дифференциальных уравнений, то есть токи и напряжения свободного режима. Запишем характеристическое уравнение цепи. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления. Запишем входное сопротивление цепи в комплексной форме.

(2.2.11)
Заменяем в выражении (2.2.11) на и приравниваем его к нулю:
(2.2.12)

Дробь равна нулю, когда числитель дроби равен нулю.
(2.2.13)
Уравнение (2.2.13) является характеристическим уравнением цепи. Характеристическое уравнение цепи можно составить другим способом. Запишем определитель исходной системы уравнений и приравниваем его к нулю:
(2.2.14)
Выполнив необходимые преобразования, получим:
(2.2.15)
Приравняв к нулю числитель выражения (2.2.15), получим:

(2.2.16)
Полученное уравнение (2.2.16) полностью совпадает с уравнением (2.2.13).

Вычислим корни характеристического уравнения: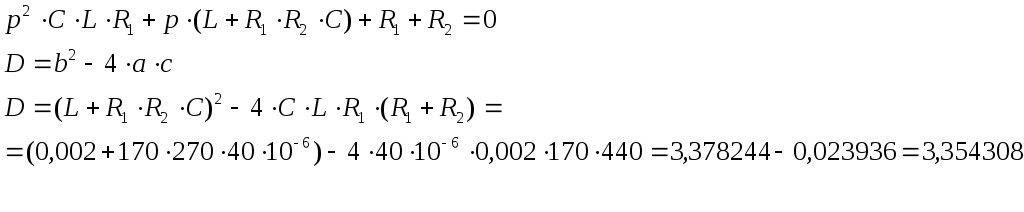
(2.2.17)

Дискриминант получился , находим корни:
(2.2.18)
(2.2.19)
(2.2.20)
Корни характеристического уравнения – вещественные числа, характер переходного процесса апериодический, свободные составляющие тока имеют вид:
(2.2.21)
где - постоянные интегрирования.
Определим зависимые начальные условия. Запишем исходную систему уравнений (2.2.8) для :
(2.2.22)
Определим значения токов :

ток - из независимых начальных условий; (2.2.23)

Так как из независимых начальных условий, то из второго уравнения находим:

(2.2.24)

Из первого уравнения:
(2.2.25)
Из третьего уравнения находим :
(2.2.26)
Для определения и продифференцируем первое и второе уравнение из системы уравнений (2.2.22) и запишем для :
(2.2.27)
Из второго уравнения системы уравнений (2.2.27) найдем :
(2.2.28)
Найдем, подставив известные числовые значения (2.2.28) и (2.2.26) в первое уравнение системы уравнений (2.2.27):
(2.2.29)
Определим постоянные интегрирования. Так как установившиеся составляющие всех токов равны нулю, то токи в цепи будут определяться только их свободными составляющими:
(2.2.30)
Продифференцируем систему уравнений для токов (2.2.30) и запишем их для :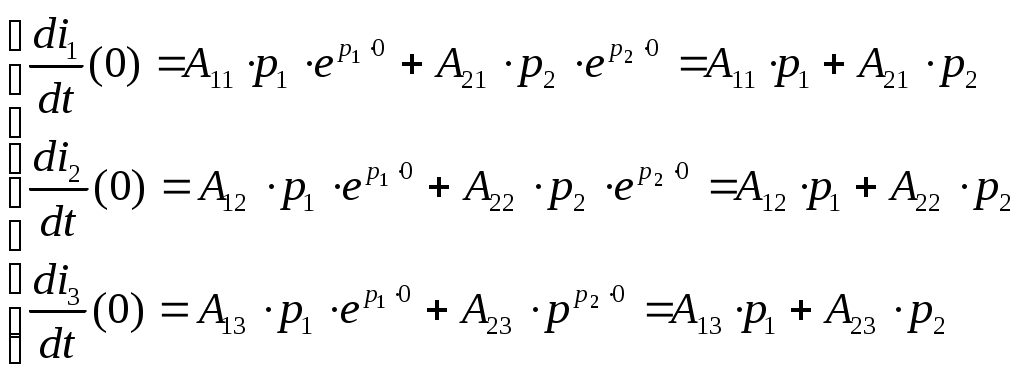
(2.2.31)

Запишем систему уравнений (2.2.30) для :
(2.2.32)

Определим постоянные интегрирования из условия:
(2.2.33)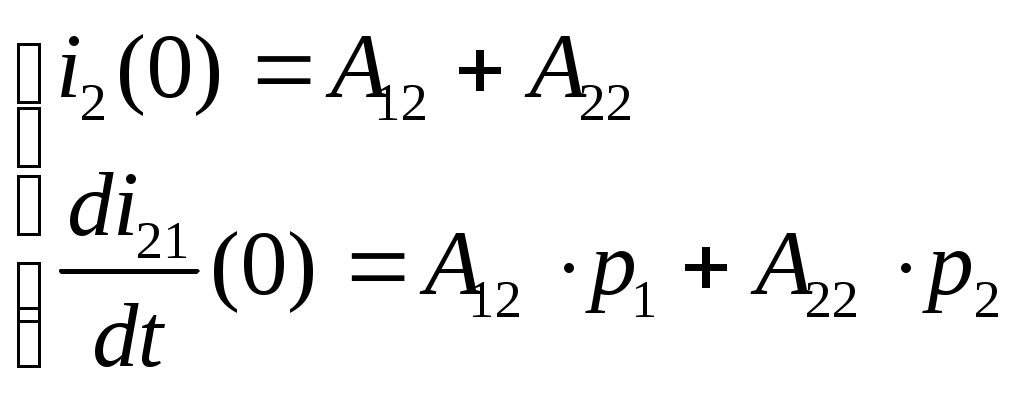

(2.2.34)
(2.2.35)
Решаем систему уравнений (2.2.33). Выражаем из первого уравнения и подставляем полученное выражение во второе уравнение той же системы уравнений:
(2.2.36)
Подставляем во второе уравнение системы уравнений (2.2.36) ранее подсчитанные значения (2.2.25), (2.2.19), (2.2.20) и (2.2.29). Преобразуем, выражение и находим значение :
(2.2.37)
Полученное значение подставляем в первое уравнение системы уравнений (2.2.36) и находим :
(2.2.38)
Решаем систему уравнений (2.2.34). Выражаем из первого уравнения и подставляем полученное выражение во второе уравнение той же системы уравнений:

(2.2.39)

Подставляем во второе уравнение системы уравнений (2.2.39) ранее подсчитанные значения (2.2.24), (2.2.19), (2.2.20) и (2.2.28). Преобразуем, выражение и находим значение :
(2.2.40)
Полученное значение подставляем в первое уравнение системы уравнений (2.2.39) и находим :
(2.2.41)
Решаем систему уравнений (2.2.35). Выражаем из первого уравнения и подставляем полученное выражение во второе уравнение той же системы уравнений:
(2.2.42)
Подставляем во второе уравнение системы уравнений (2.2.42) ранее подсчитанные значения (2.2.23), (2.2.19), (2.2.20) и (2.2.26). Преобразуем, выражение и находим значение :
(2.2.43)
Полученное значение подставляем в первое уравнение системы уравнений (2.2.42) и находим :

(2.2.44)
Полученные значения подставим в выражение (2.2.30), где (2.2.19), (2.2.20):
(2.2.45)
Для расчёта переходной характеристики в данном примере достаточно было рассчитать только третий ток. Таким образом, переходная характеристика заданного четырехполюсника имеет вид:
(2.2.46)

2.3 Определение переходной характеристики четырёхполюсника операторным методом

2.3.1 Общая схема применения операторного метода расчёта
Определим основные этапы расчёта переходной характеристики четырёхполюсника операторным методом.

1) Производится анализ цепи до коммутации и определяются независимые начальные условия. Выполняется так же, как и в классическом методе расчёта.

2) Составляется операторная эквивалентная схема цепи после коммутации. Составление операторной эквивалентной схемы производится непосредственно по эквивалентной схеме цепи для мгновенных значений путём замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений их операторными изображениями. В данной курсовой работе рассматриваются электрические цепи с нулевыми начальными условиями, поэтому операторная эквивалентная схема четырёхполюсника не содержит дополнительных независимых источников энергии, определяющих запасы энергии в цепи в момент времени, непосредственно предшествовавший коммутации.

3) Определяется операторное сопротивление четырёхполюсника Z(p) относительно его входных зажимов. Операторные сопротивления цепей записываются так же, как и сопротивления для тех цепей в комплексной форме, в которых j заменено на р.

4) Определяются операторные изображения токов в цепи, считая входным воздействием на цепь единичный скачок напряжения, описываемого единичной ступенчатой функцией (функцией Хэвисайда) 1(t), операторное изображение по Лапласу которой равно 1/р.

5) Находится выражение операторного изображения выходного напряжения четырёхполюсника.

6) Находится оригинал выходного напряжения четырёхполюсника. Поскольку изображение выходного напряжения представляет собой отношение двух полиномов р, то для выполнения обратного преобразования Лапласа целесообразно воспользоваться теоремой разложения.

7) Записывается выражение переходной характеристики по напряжению заданного четырёхполюсника. Так как внешнее воздействие на цепь в момент времени t=0 представляет собой единичный скачок напряжения, то переходная характеристика численно равна выходному напряжению четырёхполюсника.

2.3.2 Пример расчёта
Анализ цепи до коммутации и определение независимых начальных условий выполнены ранее при расчёте переходной характеристики классическим методом, из которого следует, что в начальный момент времени t=0 напряжение ёмкости и ток индуктивности равны нулю, поэтому операторные схемы замещения ёмкости и индуктивности не содержат дополнительные независимые источники энергии, характеризующие начальные запасы энергии в этих элементах.

Составим операторную схему замещения четырёхполюсника, приведённую на рисунке 2.3.1.


Рисунок 2.3.1. Операторная схема замещения четырёхполюсника
На вход цепи подадим напряжение , операторное изображение которого равно .

Запишем операторное сопротивление цепи:
(2.3.1)
Запишем операторное изображение первого тока:


(2.3.2)
Запишем операторное изображение третьего тока: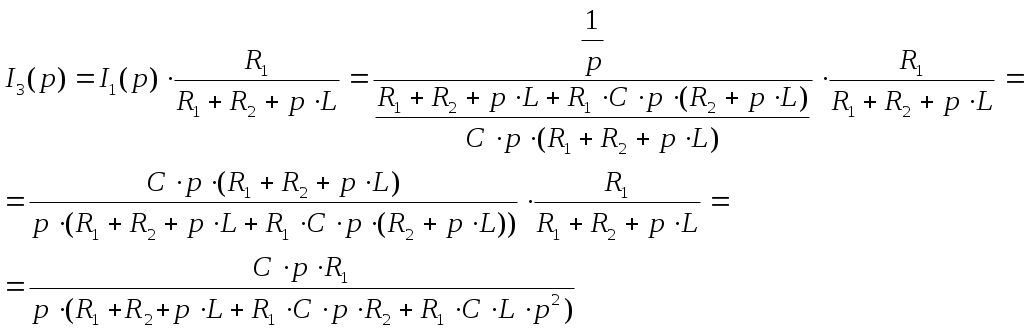

(2.3.3)
Запишем операторное изображение выходного напряжения:
(2.3.4)
Выполним обратное преобразование Лапласа, воспользовавшись теоремой разложения. Обозначим числитель и знаменатель дроби (2.3.4) соответственно и :
(2.3.5)
Приравниваем знаменатель выражения (2.3.5) к нулю - и находим корни уравнения:
(2.3.6)
Уравнение (2.3.6) абсолютно совпадает с уравнением (2.2.13), соответственно корни будут одинаковые:
(2.3.7)
(2.3.8)
Найдем производную от знаменателя дроби (2.3.5), то есть :
(2.3.9)
Применяя теорему разложения, определим оригинал выходного напряжения четырёхполюсника по формуле:

(2.3.10)
Вычислим _, подставив вместо в числитель выражения (2.3.5) первый корень характеристического уравнения (2.3.7):
(2.3.11)
В выражение (2.3.9) подставим первый корень характеристического уравнения (2.3.7) и получим:
(2.3.12)
Вычислим _, подставив вместо в числитель выражения (2.3.5) второй корень характеристического уравнения (2.3.8):
(2.3.13)
В выражение (2.3.9) подставим, второй корень характеристического уравнения (2.3.8) и получим:
(2.3.14)
Подставим найденные значения (2.3.11), (2.3.12), (2.3.13) и (2.3.14) в выражение (2.3.10), получим:
(2.3.15)
Расчеты переходной характеристики четырёхполюсника классическим методом и операторным методом практически совпадают (с учетом допустимой погрешности).

2.4 Определение импульсной характеристики четырёхполюсника операторным методом

2.4.1 Общая схема применения операторного метода расчёта
Импульсной характеристикой линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие бесконечно короткого импульса бесконечно большой высоты и конечной площади этого импульса при нулевых начальных условиях:
(2.4.1)
Импульсная характеристика цепи численно равна реакции цепи на воздействие единичного импульса .

Импульс бесконечно малой длительности, бесконечно большой высоты, площадь которого равна 1 называется единичным импульсом. Функция, определяющая единичный импульс, обозначается и называется - функцией или функцией Дирака:
(2.4.2)
При
_(2.4.3)
Для определения импульсных характеристик линейной цепи в общем случае необходимо рассмотреть переходные процессы, имеющие место в данной цепи при воздействии на неё единичного импульса напряжения. Это может быть выполнено с помощью операторного метода анализа переходных процессов.

Определим основные этапы операторного метода расчёта импульсной характеристики четырёхполюсника, считая реакцией цепи напряжение на его выходных зажимах.

1) Составляется операторная схема замещения четырёхполюсника.

2) Определяется операторное сопротивление Z(р). Можно воспользоваться произведёнными расчётами в пункте 2.3.2.

3) Определяются операторные изображения токов в цепи, считая входным воздействием на цепь единичный импульс напряжения, описываемый <sub>- функцией (функцией Дирака), операторное изображение по Лапласу которой равно 1.

4) Находится операторное изображение выходного напряжения четырёхполюсника.

5) Находится оригинал выходного напряжения четырёхполюсника, выполнив обратное преобразование Лапласа с помощью теоремы разложения.

6) Записывается выражение импульсной характеристики по напряжению заданного четырёхполюсника. Поскольку внешнее воздействие на цепь в момент времени t=0 представляет собой единичный импульс, то импульсная характеристика численно равна выходному напряжению четырёхполюсника.

2.4.2 Пример расчёта
Составим операторную схему замещения четырёхполюсника, представленную на рисунке 2.4.1.</sub>


Рисунок 2.4.1. Операторная схема замещения четырехполюсника
На вход рассчитываемой цепи подадим напряжение , операторное изображение которого равно .

Запишем операторное сопротивление цепи:
(2.4.4)
Запишем операторное изображение первого тока:
(2.4.5)

Запишем операторное изображение третьего тока:
(2.4.6)
Запишем операторное изображение выходного напряжения:
(2.4.7)
Выполним обратное преобразование Лапласа с помощью теоремы разложения. Обозначим числитель и знаменатель выражение (2.4.7) соответственно и :

(2.4.8)
Приравниваем знаменатель выражения (2.4.8) к нулю - и записываем корни уравнения:
(2.4.9)
Поскольку уравнение (2.4.9) идентично уравнению (2.2.13), то корни этого уравнения уже определены в предыдущих расчётах. Запишем числовые значения этих корней:
(2.4.10)
(2.4.11)
Найдем производную от знаменателя выражения (2.4.8), то есть :
(2.4.12)
В соответствии с теоремой разложения оригинал выходного напряжения имеет вид:
(2.4.13)
Вычислим _, подставив вместо в выражении (числитель) (2.4.8) первый корень характеристического уравнения (2.4.10):
(2.4.14)
Вычислим , подставив вместо в выражение (2.4.12) первый корень характеристического уравнения (2.4.10):
(2.4.15)
Вычислим , подставив вместо в выражении (числитель) (2.4.8) второй корень характеристического уравнения (2.4.11):
(2.4.16)
Вычислим , подставив вместо в выражение (2.4.12) второй корень характеристического уравнения (2.4.11):
(2.4.17)
Подставим найденные значения (2.4.14), (2.4.15), (2.4.16) и (2.4.17) в выражение (2.4.13):
(2.4.18)
Полученное выражение представляет собой импульсную характеристику по напряжению заданного четырехполюсника.

Графики переходной и импульсной характеристик построены в системе Mathcad 2001 Professional и приведены на рисунке 2.4.2.


Рисунок 2.4.2. Графики переходной и импульсной характеристик

2.5 Определение параметров холостого хода, короткого замыкания и - параметров четырехполюсника

2.5.1 Основные положения и соотношения
Рассмотрим линейный четырёхполюсник, не содержащий независимых источников электрической энергии. На рисунке 2.5.1 обозначим принятые положительные направления для токов и напряжений на выводах четырёхполюсника.


Рисунок 2.5.1. Положительное направление токов и напряжений четырехполюсника
Вариант с токами и называется прямой передачей, вариант с токами и называется обратной передачей.

Соотношения между напряжениями и токами на входе и выходе четырёхполюсника могут быть записаны в виде одной из шести форм основных уравнений: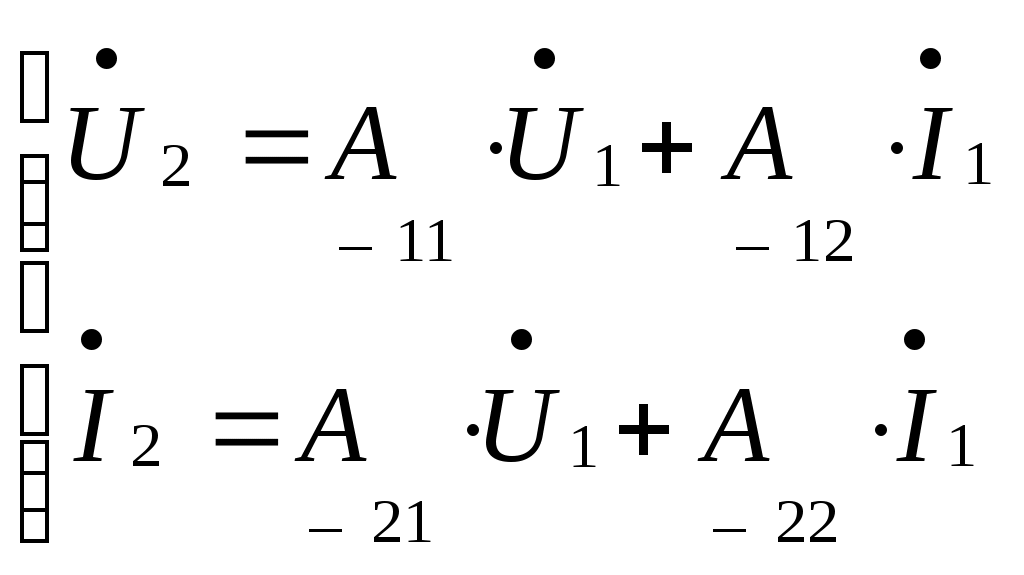
(2.5.1)
Коэффициенты при напряжениях и токах в основных уравнениях четырёхполюсника называются первичными параметрами четырёхполюсника, они определяются только схемой самого четырёхполюсника.

Коэффициенты в общем случае комплексные и зависят от частоты. Эти коэффициенты могут быть определены следующим образом:

а) по известным значениям напряжений и токов четырёхполюсника в режимах холостого хода и короткого замыкания:
- отношение напряжений при разомкнутых выходных выводах;
- отношение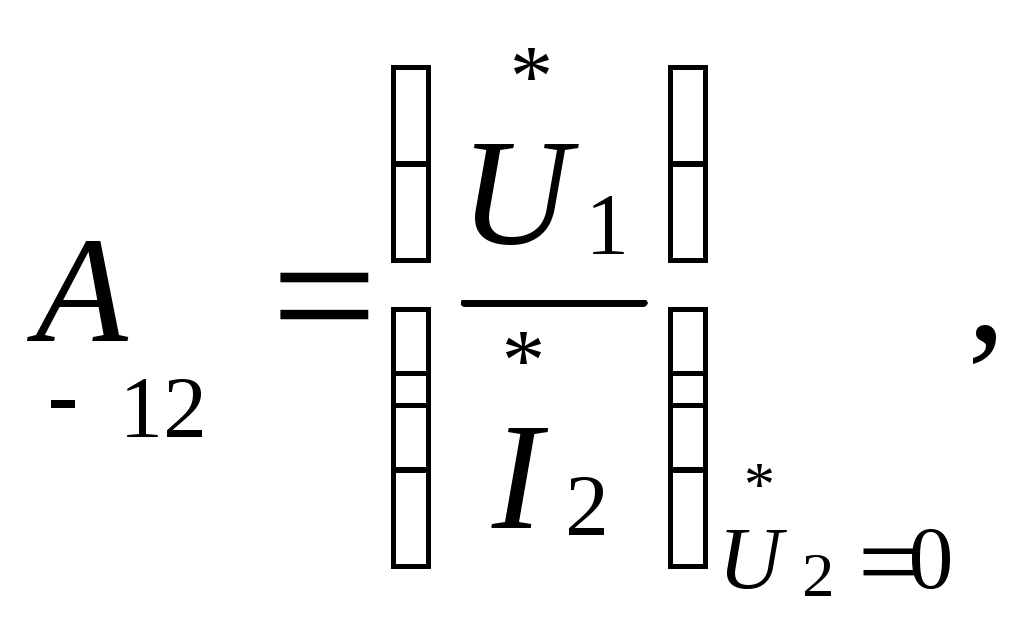 токов при закороченных выходных выводах;
- величина, обратная передаточной проводимости при закороченных выходных выводах;
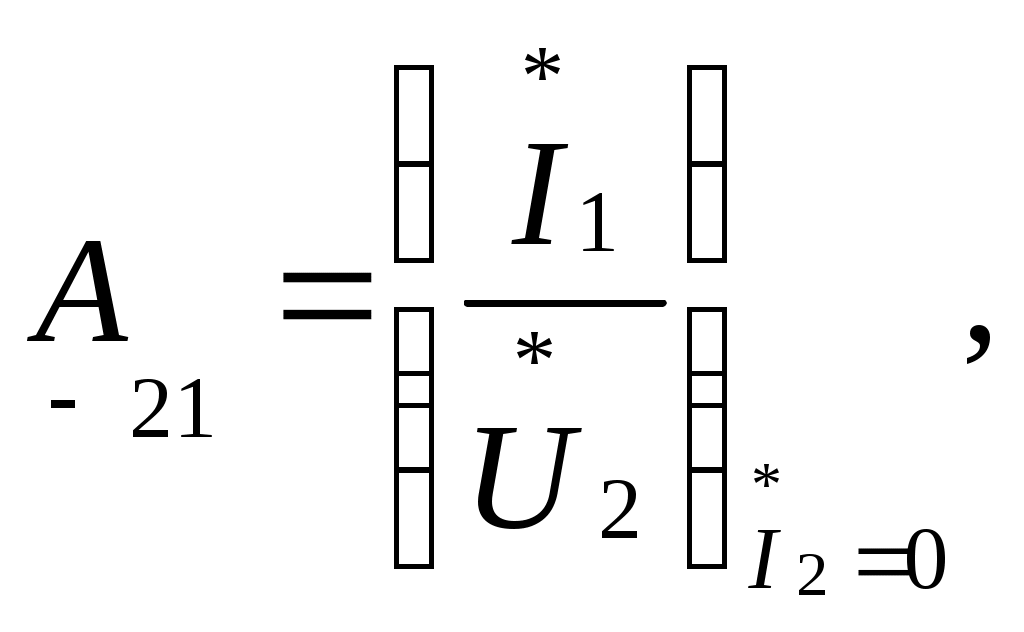- величина, обратная передаточному сопротивлению

при разомкнутых выходных выводах; (2.5.2)
б) через параметры холостого хода и короткого замыкания:


_(2.5.3)




В курсовой работе расчет - параметров следует выполнить через параметры холостого хода и короткого замыкания, то есть для заданного четырёхполюсника необходимо рассчитать следующие сопротивления:

- входное сопротивление четырёхполюсника со стороны выводов 1 -1’ при разомкнутых выводах 2 – 2’;

- входное сопротивление четырёхполюсника со стороны выводов 2 – 2’ при разомкнутых выводах 1 - 1’;

- входное сопротивление четырёхполюсника со стороны выводов 1 – 1’ при закороченных выводах 2 – 2’;

- входное сопротивление четырёхполюсника со стороны выводов 2 – 2’ при закороченных выводах 1 – 1’.

После расчёта параметров холостого хода и короткого замыкания по формулам (2.5.3) определяются коэффициенты _.

Правильность расчёта проверяется соотношением (2.5.4)


2.5.2 Пример расчёта

Комплексная схема замещения четырёхполюсника приведена на рисунке 2.5.2.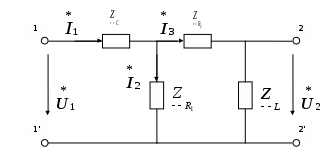



Рисунок 2.5.2. Комплексная схема замещения четырёхполюсника
Определим комплексное сопротивление :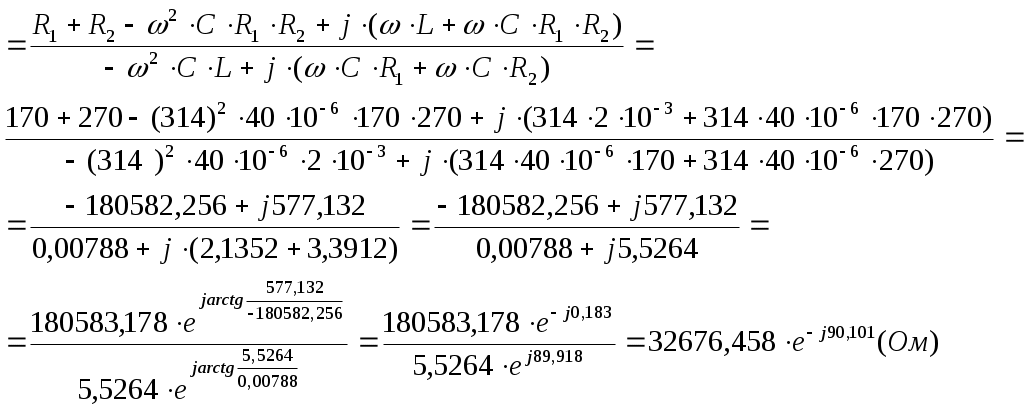



(2.5.5)

Определим комплексное сопротивление :
(2.5.6)
Определим комплексное сопротивление для цепи, приведённой на рисунке 2.5.3.



Рисунок 2.5.3. Распределение токов в режиме короткого замыкания со стороны зажимов 2 – 2’
Так как выводы 2 – 2’ соединены короткозамкнутой перемычкой, то ток третий, протекающий через резистор _, не будет проходить через катушку, а пойдет по пути наименьшего сопротивления, то есть через короткозамкнутый участок.

Комплексное сопротивление имеет вид:
(2.5.7)
Определим комплексное сопротивление для цепи, приведённой на рисунке (2.5.4).


Рисунок 2.5.4. Распределение токов в режиме короткого замыкания со стороны зажимов 1 -1’
Комплексное сопротивление имеет вид:




(2.5.8)
Используя значения , определяем - параметры по формулам (2.5.3):

(2.5.9)
(2.5.10)
(2.5.11)
(2.5.12)
Проверяем правильность расчетов - параметров, используя тождество :
(2.5.13)
Можно сделать вывод, что расчеты выполнены правильно с учетом допустимой погрешности.

2.6 Определение характеристических параметров четырехполюсника

2.6.1 Основные положения и соотношения
К характеристическим параметрам четырёхполюсника относятся: характеристические сопротивления и , характеристическая (собственная) постоянная передачи , которые полностью характеризуют четырёхполюсник.

На рисунке 2.6.1 приведена схема несимметричного четырёхполюсника при прямой и обратной передаче.



Рисунок 2.6.1 - Несимметричный четырехполюсник при прямой и обратной передаче (а и б - произвольная нагрузка; в и г - согласованная нагрузка)
Положим, что сопротивления и в схемах рисунок 2.6.1 а) и б) подобраны таким образом, что и . Иначе говоря, будем считать, что существуют два сопротивления: и , которые удовлетворяют следующему условию: входное сопротивление четырехполюсника, нагруженного сопротивлением , равно (рисунок 2.6.1, в); входное сопротивление четырехполюсника, нагруженного сопротивлением , равно (рисунок 2.6.1,г). 

Такие два сопротивления называются