МУ к выполнению курсовой работы. Методические указания Саратов введение цель работы практическое освоение методов проектирования сварных конструкций (СК)
 Скачать 0.6 Mb.
|
|
4. Определение размера сечения балки Для балки основной нагрузкой является изгибающий момент. Условие прочности  , (6)где [σ], как и в разделе. 3, равно меньшему из двух значений –  (см. формулу (3) ) или Ry ( см. формулу (4)). Обычно один из моментов существенно меньше другого, и при выборе сечения его можно не учитывать для упрощения расчета, так же как и напряжения от продольной силы (My=0; Pz=0). Основную часть нагрузки при изгибе воспринимают полки балки. Металл полок работает на изгиб в 3 раза эффективнее, чем металл стенок. Для анализа работы различных сечений (см. рис.2) представим каждое из них состоящим из одной или двух стенок, высота которых равна высоте всей балки, и двух полок, которые включают в себя всю оставшуюся часть сечения (рис. 4). К такой схеме можно свести все 3 типа сечений, предназначенных для балок в вариантах задания. Найдем вначале площадь и момент инерции сечения стенок. Для обеспечения местной устойчивости стенки (см. раздел 8) при отсутствии сжимающих ее сосредоточенных сил необходимо выполнить условие  , где  . Для ВСт3сп  .Таким образом, суммарная площадь сечения стенок  , (7)где n – число стенок в сечении (1 или 2). Суммарный момент инерции стенок 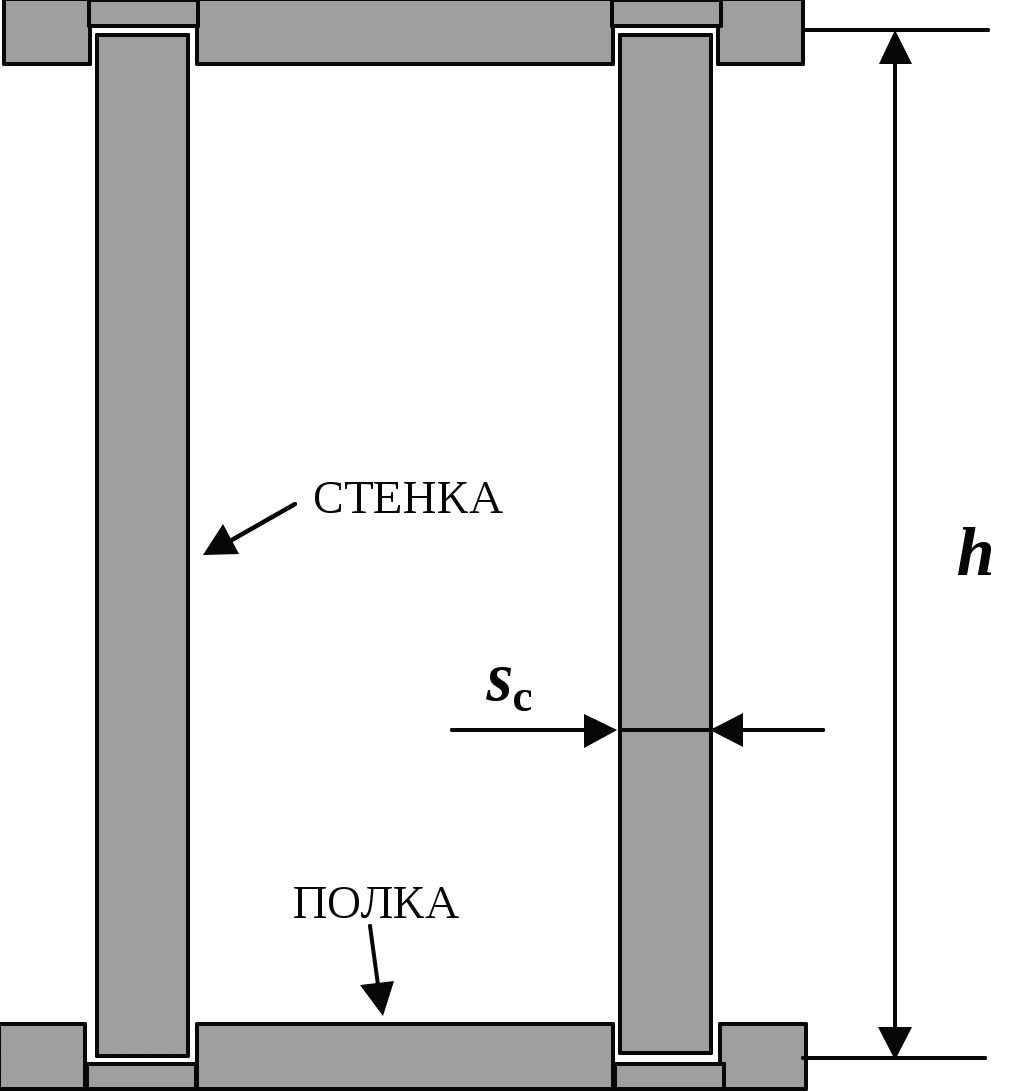 . (8) Рис.4. Схематизация сечения балки: 2 полки +1 или 2 стенки Момент инерции всего сечения  должен быть не менее требуемого из условия прочности (6)  . (9)Если высота балки  , то момент инерции стенок (без полок) меньше требуемого:  . Полки должны обеспечить недостающий момент инерции  . Из формулы  (10)(моментом инерции полки относительно ее центра можно пренебречь) найдем необходимую для этого суммарную площадь сечения двух полок  . Тогда площадь сечения всей балки, найденная из условия прочности .По мере роста h (высоты балки),  вначале снижается за счет уменьшения сечения полок, а затем вновь растет за счет роста сечения стенок. Оптимальную высоту балки hσможно найти из условия прочности при минимуме площади сечения: ;  ;  Для двутавровой балки или одиночного швеллера n = 1, и ее оптимальная высота из условия прочности (для ВСт3сп)  . (11)Для коробчатой балки или пары швеллеров n = 2,  . (12)Кроме рассмотренного условия прочности балки существует условие жесткости. Балка в конструкции обычно создает жесткую ровную опору для пола в здании, для тележки крана и т.д. Уклон не должен превышать предельного значения, которое задают в виде прогиба на единицу длины балки. Предельный прогиб (вертикальное перемещение незакрепленного конца балки), приведенный в задании, равен 20 мм. Уравнение, описывающее прогиб консольной балки, можно найти в справочнике или вывести, используя методы сопромата:  . Из этого уравнения находят требуемый момент инерции (13)Далее, используя формулы (7,8,10), получим для двутавровой балки оптимальную высоту из условия жесткости:  ;  ; ;  ;  .Для двутавровой балки или одиночного из ВСт3сп  . (14)Для коробчатой балки или пары швеллеров  . (15)Теперь необходимо совместить полученные решения с учетом одновременно и жесткости и прочности. Из сопоставлении требуемых моментов инерции, найденных из условий прочности (9) и жесткости (13) и условия следует, что при малых значениях h условие прочности требует меньшего момента инерции, чем условие жесткости, а при больших h - большего (рис.5). Из условия равенства требуемых моментов инерции  можно определить высоту балки, при которой выполняется с одинаковым коэффициентом запаса и условие прочности, и условие жесткости . (16) Из рис. 5 ясно, что при h > h* запас прочности больше, чем жесткости, а при h < h* - наоборот. Поэтому при h < h* расчет следует вести только на жесткость, а при h > h* только на прочность. То есть h* - это порог высоты балки, до которого действуют уравнения жесткости (13 - 15), а свыше - уравнения прочности (9, 11, 12). Возможны 3 сочетания hf, h* и hσ. Если hf < h*, то оптимальной является высота балки h = hf; если hσ> h*, то оптимальной является высота балки h = hσ (этот случай показан на рис.5); если hσ< h* < hf, то оптимальной является высота балки h = h*. Если полученная оптимальная высота больше габаритной hmax, то принимают h = hmax, но сечение и масса в этом случае увеличиваются. После выбора значения h остальные размеры сечения выбрать проще. Следует найти Ix по формуле (13), если h < h*, или по (9), если h > h*. Затем определить момент инерции стенки (или стенок, если балка коробчатая) по формуле (7). Остальная часть момента инерции приходится на полки - Iп. Зная Iп, по формуле (10) рассчитывают Aп. Толщину полок выбирают, как правило, больше, чем стенок, (от 10 до 30 мм). 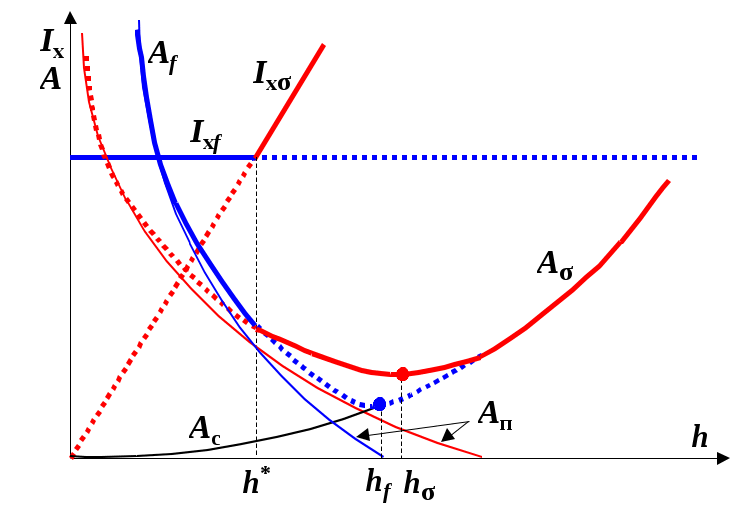 Рис. 5. Зависимость требуемых момента инерции и площади сечения от высоты балки по условиям прочности (σ) и жесткости (f).При выборе толщины стенок и полок следует учитывать, что уменьшение толщины стенки уменьшает массу балки, но может привести к местной потере устойчивости стенки. Уменьшение толщины полки и увеличение ее ширины улучшает общую устойчивость балки и ее работу на изгиб в горизонтальной плоскости, но может также привести к потере местной устойчивости в полке. По этим причинам может потребоваться корректировка выбранных размеров при проверочных расчетах (см. разделы 7 и 8). 5. Проверочный расчет на прочность При проектном расчете сечений стойки и балки был использован ряд упрощений и допущений, облегчающих расчет. В связи с этим необходимо проверить прочность подобранного сечения. Основным напряжением в стойках и балках является продольное нормальное напряжение σ, возникающее от продольной силы Pz и изгибающих моментов Mx и My. После того как все размеры сечения определены, его можно вычислить по формуле (6). В формулу необходимо подставить значения координат x и y опасных точек сечения, в которых возникают наибольшее растягивающее и наибольшее сжимающее напряжения σ. Эти напряжения не должны превосходить допускаемых напряжений, найденных по формулам (3, 4). Кроме того, в сечении действуют касательные напряжения от поперечной силы Qy.  , (17)где AQ - суммарная площадь элементов сечения, плоскость которых параллельна линии действия Qy. Условие прочности  (18)необходимо проверить в двух точках: на краю полки (σ=σmax,τ= 0) и в месте присоединения полки к стенке(σ<σmax,τ>0).Согласно СНиП, сечение спроектировано рационально, если условия прочности выполнены, причем в наиболее опасной точке превышение допускаемых напряжений над действующими в сечении не превосходит 5%. Если прочность не обеспечена, то необходимо увеличить его размеры. Если излишний запас прочности превышает5%, следует попытаться уменьшить площадь сечения и массу конструкции. 6. Проверочный расчет общей устойчивости стоек Такая проверка требуется только при действии сжимающих продольных сил. Если силы приложены к центру сечения (Mx= My= 0), то снижение статической прочности стойки за счет потери устойчивости оценивают коэффициентом φ, зависящим от гибкости стойки. Гибкость стойки относительно материальной оси (т. е. оси, пересекающей элементы сечения) определяют по формуле  (19)где ℓ - длина полуволны изогнутой оси стойки,  . Коэффициент μ зависит от условий закрепления. Чем больше промежуточных закреплений, тем меньше гибкость при той же длине стойки L. Для стойки, шарнирно закрепленной по концам (стойки Эйлера), имеющей форму изгиба, близкую к полуволне синусоиды, μ = 1. Для других схем закрепления также можно определить μ и ℓ, рассматривая любую стойку, как состоящую из стоек Эйлера или как часть стойки Эйлера. В случае консольного закрепления длина полуволны равна 2L и μ = 2. Радиус инерции является характеристикой сечения и показывает, на какое расстояние в среднем удалены точки сечения стойки от оси возможного изгиба. Изгиб происходит в направлении наибольшей гибкости стойки, т. е. вокруг оси, относительно которой момент инерции наименьший. Если сечение состоит из четырех уголков, то по значению imin близок к половине минимального габаритного размера поперечного сечения и почти не зависит отсечения уголка. Если сечение стойки составное и изгиб происходит относительно свободной оси, то за счет нежесткого соединения ветвей ее гибкость больше, чем полученная по формуле (19), поэтому используют приведенную гибкость  ,где λ - гибкость, вычисленная по формуле (19). Если сечение состоит из двух ветвей и имеет только одну свободную ось, то λ2= 0. Если ветви соединены планками, то λ1 - гибкость ветвей относительно оси 1 (см. рис. 2), параллельной оси изгиба и проходящей через центр сечения ветви (центральной оси ветви). Относительно оси 1 определяют радиус инерции ветви i1 при расчете λ1:  .Длина ℓ1 при этом равна расстоянию между серединами планок (рис. 6,а). 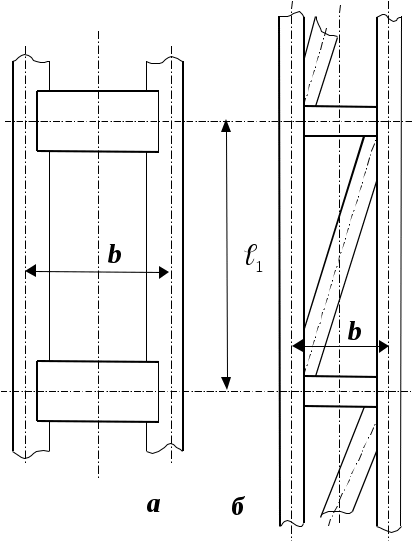 Рис.6. длины элементов стойки с составным сечением: а - с соединительными планками, б - с решеткой. Если ветви соединены решеткой (рис. 6,б), то  где A – площадь сечения всей стойки; Ad1- – площадь сечения раскоса, лежащего в плоскости, перпендикулярной оси 1; a - длина раскоса, b - расстояние между осями 1 двух ветвей. Если сечение имеет четыре ветви и две свободных оси, то λ2 определяют так же, как λ1, но относительно оси 2, проходящей через центр сечения ветви перпендикулярно оси изгиба. Расстояния между планками ℓ1 подбирают так, чтобы гибкость ветви была не более 80, т. е.  где imin - минимальный радиус инерции одной ветви. При малой гибкости стойки (λ< 10) допускаемое напряжение близко к статической прочности материала [σ] →Ry, а φ→ 1.При большой гибкости (λ> 100) допускаемое напряжение зависит только от одной характеристики материала - от модуля упругости. Так как все стали имеют примерно одинаковый модуль упругости, то допускаемое напряжение мало зависит от марки стали. Значит, применение высокопрочных сталей при большой гибкости сжатой стойки нерационально. Коэффициент φ учитывает это явление, и значения φ при большой гибкости таковы (табл. 72 приложения 6 СНиП), что произведение Ry·φ при λ> 100 практически не зависит от Ry. Для стали ВСт3сп (Ry≈238 МПа) φ можно определить по сокращенной табл. 6, как функцию только от наибольшей гибкости λmax. Таблица 6
|