МУ к выполнению курсовой работы. Методические указания Саратов введение цель работы практическое освоение методов проектирования сварных конструкций (СК)
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Саратовский государственный технический университет РАСЧЕТ И ПРОЕКТИРОВАНИЕ СТЕРЖНЕВЫХ СВАРНЫХ КОНСТРУКЦИЙ Методические указания Саратов ВВЕДЕНИЕ Цель работы - практическое освоение методов проектирования сварных конструкций (СК). Методические указания базируются на материалах СНиПа [1]. Для освоения методов проектирования предлагается разработать простейшую сварную конструкцию, представляющую собой стержень, нагруженный двумя силами: поперечной и сжимающей внецентренной продольной (рис.1). Такая конструкция широко применяется в строительстве, в машиностроении и в других отраслях производства в виде отдельного изделия и в виде элемента рамы или фермы. В курсовой работе предполагается проводить расчёт СК на выносливость, прочность сварных швов и устойчивость сжатых элементов. В зависимости от соотношения сил и создаваемых ими моментов стержень работает как стойка (на сжатие), либо как балка (на изгиб), что требует расчета СК по формулам на прочность и жесткость [1]. Задача состоит в разработке рациональной конструкции, обеспечивающей прочность и жесткость при наименьших массе и стоимости. Для ее успешного решения необходимо ясное представление о том, какие параметры конструкции подлежат выбору в процессе проектирования и как этот выбор влияет, с одной стороны, на прочность, устойчивость и жесткость, а с другой – на массу и стоимость. Как правило, проектировщик имеет возможность выбора: типа поперечного сечения (сплошного или составного из двух или четырех ветвей); - вида заготовок (листов, гнутых или прокатных профилей); - марки стали или сплава; - размеров элементов сечения и расстояний между ними; - способа соединения элементов сечения (стыковыми или угловыми швами, непосредственно или через промежуточные элементы); - конструктивного оформления сварных узлов. . 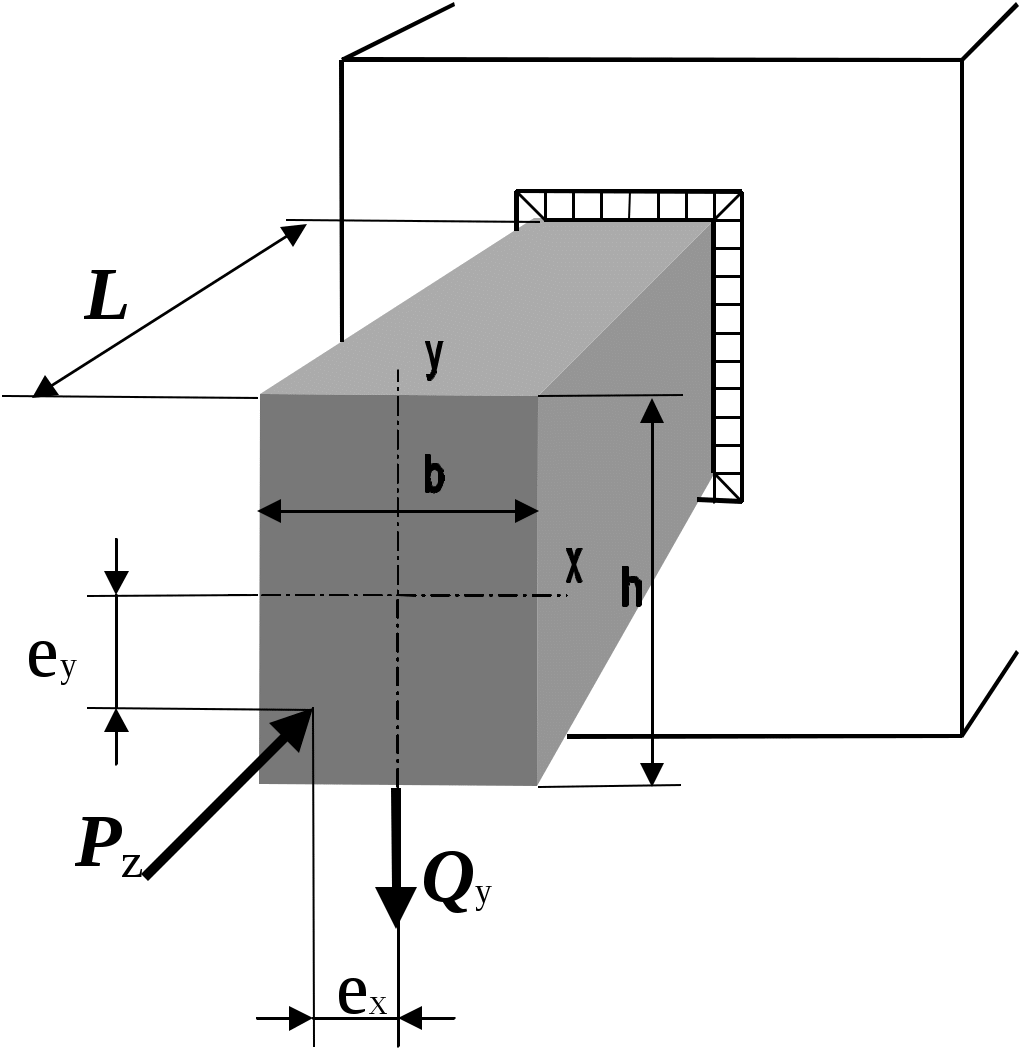 Рис. 1. Схема приложения сил к стержневой конструкции ИСХОДНЫЕ ДАННЫЕ Стержневая конструкция (см. рис.1) одним концом жестко прикреплена к стенке, нагружена продольной силой Pz и поперечной Qy (x,y - главные оси поперечного сечения, z – продольная ось). Сила Pz приложена внецентренно, с эксцентриситетами ex и ey (ey > 0 при приложении силы Pz ниже центра сечения). Значения силы Pz для разных вариантов задания приведены в табл.1, значения силы Qy и эксцентриситетов - в табл. 2. Таблица 1
Таблица 2
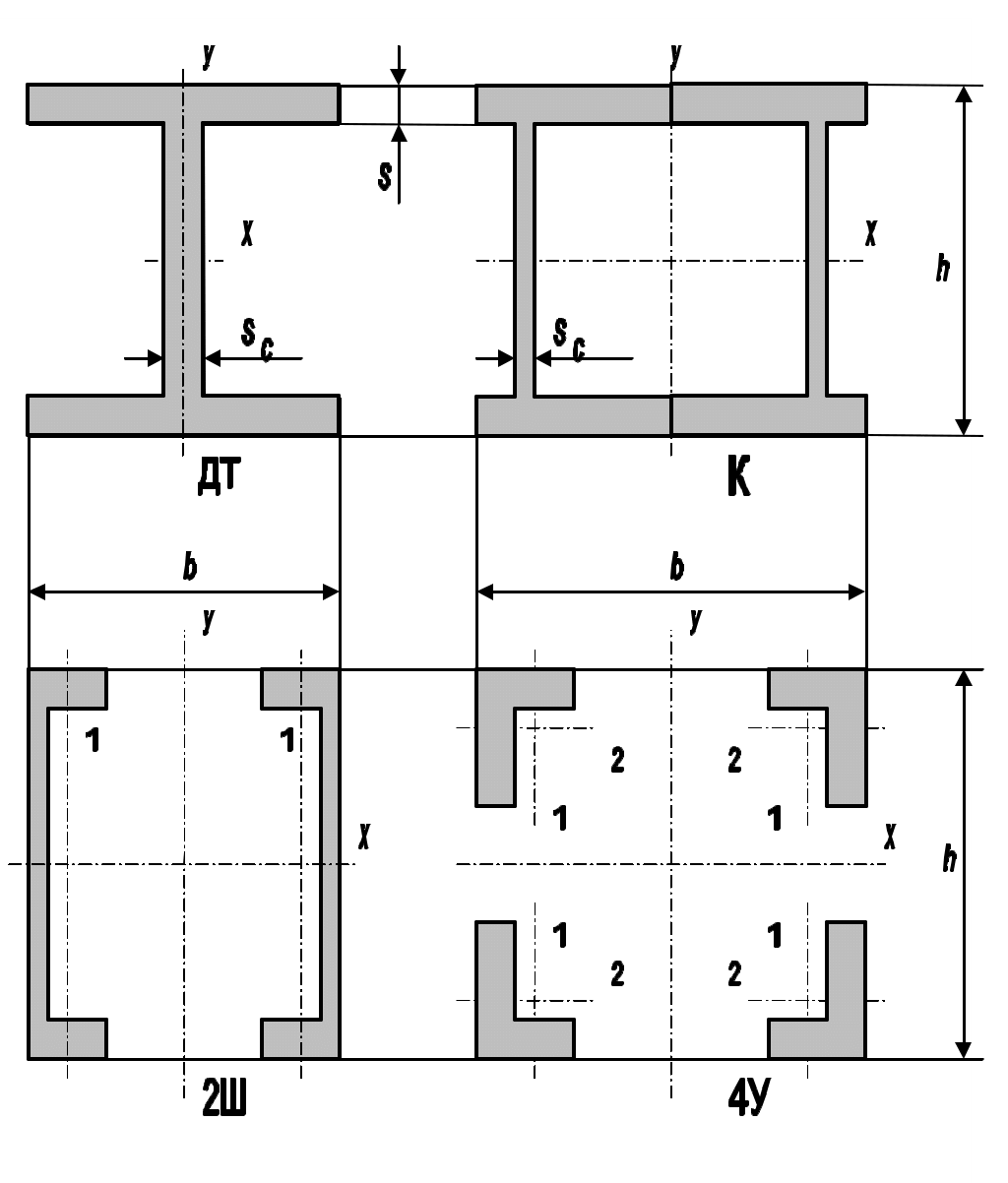
Предлагаемые типы поперечных сечений для разных вариантов задания приведены на рис.2 и в табл.3. Поперечное сечение ограничено габаритами hmax и bmax, значения которых для двух подвариантов приведены в табл.4. Длина стержня L=2 м. Материал - сталь ВСтЗсп. Нагрузка циклическая, пульсирующая (с коэффициентом асимметрии цикла ρ=0), число циклов за срок службы n=106. При работе на выносливость наибольшую концентрацию напряжений создают угловые швы, присоединяющие конструкцию к стенке (6-я группа по СНиП). Максимальное поперечное перемещение свободного конца при расчете на жесткость f=L/100=20 мм.
Таблица 3
Таблица 4
II. ЗАДАНИЯ Задание 1 а) Построить эпюры изгибающих моментов и поперечных сил. Определить относительные эксцентриситеты приложенной нагрузки согласно СНиП и по их значениям установить, работает конструкция как балка или как стойка. В зависимости от этого выбрать тип поперечного сечения по табл. 3. б) Подобрать размеры сечения, обеспечивающие прочность, устойчивость и жесткость конструкции при наименьшей массе. Определить массу конструкции, включая соединительные планки и ребра жесткости. в) Подобрать размеры сечения с габаритами hmax и bmax,для подварианта А в 1,5 раза меньшими, а для подварианта Б в1,5 раза большими, чем заданные в табл. 4. Сопоставить массу двух вариантов конструкции. Задание 2 а) Спроектировать сварной узел, обеспечивающий прикрепление стержневой конструкции. Проверить прочность всех сварных швов. б) Определить массу наплавленного металла. в) Вычертить конструкцию в масштабе, в трех проекциях, с указанием размеров, с необходимыми разрезами и сечениями. III. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ 1.Анализ расчетной схемы Выбор сечения, обеспечивающего прочность и жесткость конструкций при минимальной массе, зависит от соотношения действующих на нее продольных и поперечных сил и моментов. При действии только продольной растягивающей силы Pz (см. рис. 1), приложенной по оси симметрии сечения, форма сечения может быть любой. Площадь сечения и масса конструкции, необходимые для обеспечения прочности, от формы сечения не зависят, так как напряжения по сечению распределены равномерно и все части сечения одинаково участвуют в передаче силы. При действии поперечной силы Qy дело обстоит иначе. Рассмотрим стержень в виде уголка из листовых элементов, один из которых обращен к линии действия силы Qy ребром, а другой плоскостью (рис.3). Жесткость этих элементов при сдвиге различна. При действии одинаковых касательных напряжений τ1= τ2 в сечении элемент, обращенный плоскостью к линии действия силы, прогнется сильнее, чем более жесткий, обращенный к ней ребром (Δ2 » Δ1). 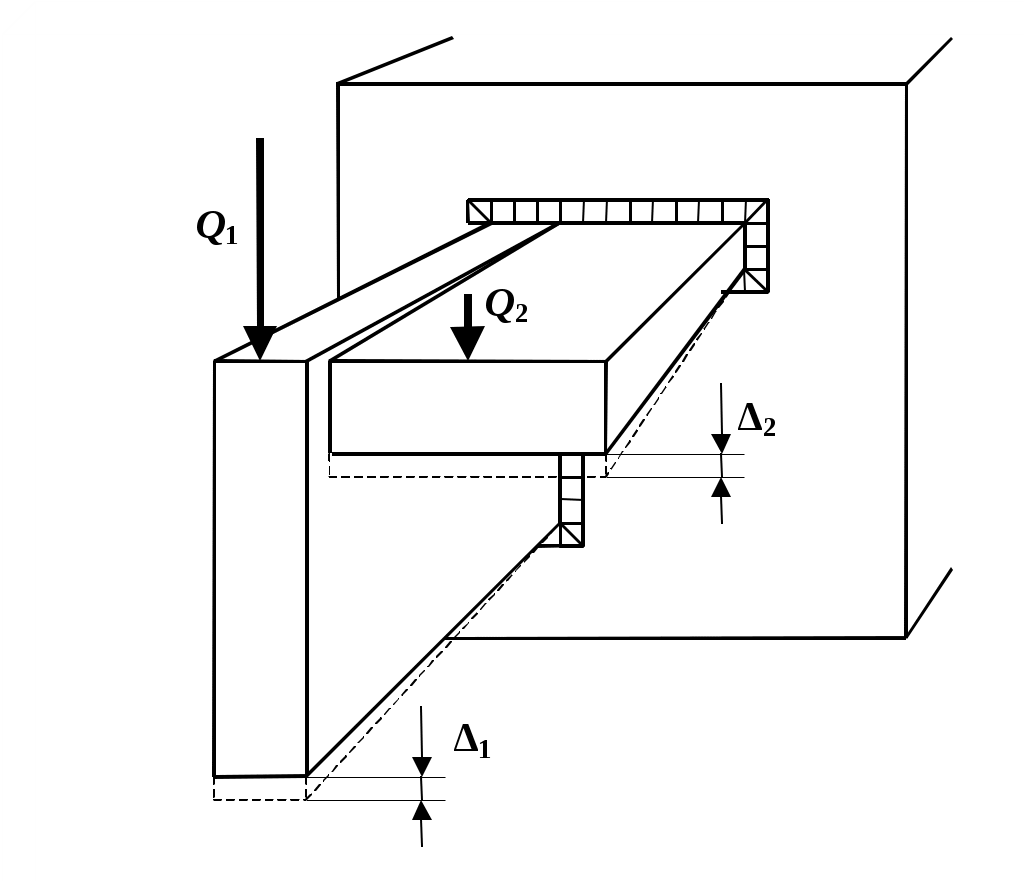 Рис. 3. Схема работы уголка на срез. Так как в действительности листовые элементы соединены между собой, образуют единое сечение и имеют одинаковый прогиб (Δ1 = Δ2), то, следовательно, напряжения распределены неравномерно (τ1 » τ2). Основную часть силы Qy воспринимает более жесткий элемент (Q1 » Q2), в нем напряжения больше, и только от его сечения зависит прочность всей конструкции при работе на срез при действии силы Qy. При действии изгибающего момента важно не только, какие напряжения возникают в отдельных частях сечения, но и на каком расстоянии эти части сечения находятся от оси изгиба. Чем больше расстояние, на котором находится некоторая часть сечения, тем больше плечо силы, передаваемой этой частью сечения и тем больше ее участие в работе конструкции на изгиб. Однако сечение должно быть единым, поэтому нужен элемент, соединяющий части сечения, передающие изгибающий момент и разнесенные как можно дальше от оси. Примером наиболее эффективного сечения при изгибе является двутавр (см. рис. 2). Изгибающий момент передают полки двутавра, одна из которых растянута, а другая сжата. Стенка двутавра при чистом изгибе слабо нагружена, поэтому ее делают более тонкой, чем полки. При поперечном изгибе от действия силы Qy (см. рис. 1) в сечениях возникают одновременно изгиб и срез. Изгиб воспринимают полки, а срез - стенка. Коробчатое сечение менее эффективно при изгибе, так как имеет две стенки, и, следовательно, его площадь больше. Однако оно эффективнее, чем двутавровое при изгибе в двух направлениях вокруг осей x и y и при работе на кручение вокруг оси z. Изгиб стержня возникает при действии поперечных сил, а также в случае внецентренного приложения продольной силы. При внецентренном растяжении деформация стержневой конструкции под нагрузкой приводит к уменьшению эксцентриситета, выпрямлению продольной оси стержня и приближению ее к линии действия силы. В случае сжатия эксцентриситет и искривление под нагрузкой увеличиваются, что может вызвать потерю устойчивости: общую (всей конструкции) или местную (сжатых частей сечения, имеющих малую жесткость и сильно искривляющихся). Поскольку причиной потери устойчивости является изгиб, то меры для обеспечения устойчивости и жесткости те же, что и для обеспечения прочности при изгибе: части сечения должны быть разнесены как можно дальше от возможной оси изгиба. Это достигается при обеспечении общей устойчивости применением коробчатых и составных сечений, а при обеспечении местной устойчивости - усилением поперечными ребрами сжатых элементов сечения. Приведенные соображения по выбору наилучшего сечения в зависимости от вида нагрузки показывают, что причины разрушения при растяжении, срезе, изгибе и сжатии различны и объясняют, почему по СНиП для расчета одной и той же стержневой конструкции в этих случаях применяют разные формулы. Растянутые стойки рассчитывают только на прочность, изогнутые балки и сжатые стойки - на прочность, жесткость и устойчивость. Как правило, на конструкцию действуют и продольная сила, и изгибающий момент. В этом случае расчетную схему (стойки или балки) уточняют по относительному эксцентриситету, равному отношению напряжений от изгиба к напряжениям от сжатия: , (1) где A - площадь сечения, а Wx – его момент сопротивления относительно оси x. Для сплошного прямоугольного сечения д ля коробчатого или двутаврового сечения с толстыми полками и тонкими стенками для произвольного сечения где Чем выше α, тем лучше работает сечение на изгиб и устойчивость. Из этих формул следует, что увеличение площади полок двутавра, швеллера или коробчатого сечения даст в 3 раза большее увеличение момента сопротивления изгибу Wx, чем такое же увеличение площади стенок. Приняв α≈0,8; h=hmax, можно по исходным данным найти mx. Для определения MXmax необходимо построить эпюру изгибающих моментов в стержне. А налогично рассчитывают относительный эксцентриситет my: Если наибольший из относительных эксцентриситетов mx и my имеет значение менее 0,1, то стойка по СНиП считается центрально сжатой (растянутой); если от 0,1 до 5 - внецентренно сжатой (растянутой); если m>20 ,то стержневой элемент является изгибаемой балкой,растяжением и сжатием которой можно пренебречь; если m от 5 до 20, то растяжение или сжатие балки необходимо учитывать в расчете. 2. Выбор типа поперечного сечения Для балок выбирают, как правило, сечение в виде двутавра (ДТ), двух швеллеров (2Ш) или коробчатое (К) (см. рис. 2), причем сечение располагают так, чтобы наибольший изгибающий момент действовал относительно оси, обозначенной на рис.2 как ось x. Как отмечено в п. 1, двутавровое сечение имеет большую жесткость только относительно оси x, поэтому его следует применять, когда изгибающий момент My во много раз меньше, чем Mx. Такие же сечения применяют и для стоек, причем если сжатие стойки внецентренное (с изгибом), то сечение располагают так, чтобы изгиб происходил вокруг оси x (см. рис. 2). Но в большинстве случаев для стоек наиболее экономичными оказываются составные сечения из двух (2Ш) или четырех (4У) ветвей, соединенных планками или решеткой из вспомогательных элементов. Увеличивая расстояния между ветвями, можно повысить жесткость сечения на изгиб без роста площади сечения. Однако при этом растут длина, сечение и масса вспомогательных элементов, соединяющих ветви, причем их суммарная масса может превысить массу ветвей сечения, особенно при значительной поперечной силе Qy. Балки всегда имеют в сечении стенку, соединяющую полки, т. е. ось x у балки является материальной, а свободной может быть только ось y (ДТ, 2Ш, К на рис.2). Это связано с тем, что балки применяют при действии существенной поперечной силы Qy и сосредоточенных поперечных сил (например, от тележки крана, перемещающейся по полке балки). В исходных данных работы выбор типа сечения ограничен. Для каждого варианта предложен один тип сечения, если конструкция является стойкой, и другой - если она работает как балка (см. п. 1). Сечение следует расположить так, чтобы ось, обозначенная x на рис.2, совпадала с осью наибольшего изгибающего момента Mmax, определяемого по эпюре. Расчет размеров сечения является весьма сложной операцией и в некоторых случаях осуществляется методом подбора: задают произвольные размеры сечения и проводят проверку конструкции на прочность и жесткость. Если прочность и жесткость не обеспечены, то увеличивают размеры сечения, а если обеспечены с большим запасом - уменьшают. Для сокращения числа попыток желательно подобрать сразу сечение, близкое к необходимому. Для этого при проектировании балок и стоек используют различные приемы. 3. Определение размера сечения стойки Основной нагрузкой для стойки является продольная сила. Поэтому для выбора сечения используют расчет на прочность при растяжении (сжатии): (2) Из этого уравнения находят требуемую площадь поперечного сечения . (3) Допускаемое напряжение [σ] при работе на выносливость зависит от марки стали, концентрации напряжений в сечении, числа циклов нагружения и асимметрии цикла. В СНиП допускаемое напряжение при работе на выносливость определяют по формуле Расчетное сопротивление Rv зависит от концентрации напряжения и от предела текучести материала. Концентрация напряжений в сварных соединениях чаще всего обусловлена сварными швами. Значение коэффициента концентрации зависит от формы, размеров и расположения швов. Чем выше концентрация напряжений, тем ниже допускаемое напряжение. В СНиП концентрация напряжений учитывается приближенно. Все типы сварных соединений разбиты на восемь групп. Независимо от формы и размеров швов и свариваемых элементов, сварное соединение относят к одной из этих групп. В пределах группы концентрация напряжений принимается постоянной. Наименьшую концентрацию напряжений имеют соединения из 1-й группы, наибольшую из 8-й. Чтобы определить номер группы для конкретного узла, необходимо воспользоваться табл. 83 приложения 8 СНиП. Выдержки из этой таблицы для стали ВСт3сп приведены в табл.5. Таблица.5
При резком изменении ширины полосы 1-я группа сохраняется, если радиусы галтелей не менее 200 мм. При уменьшении радиуса до 10 мм номер группы повышается до четвертого. Концентрация напряжений у конца косынки, приваренной встык или втавр, зависит от угла при вершине косынки. Если он менее 45º, то группа 4-я, а при увеличении угла до 90º номер группы увеличивается до седьмого. При наличии в сечении нескольких концентраторов, в расчете используют самый большой номер группы. В пределах одной группы Rv зависит от марки стали. Чем выше ее предел прочности, тем выше Rv. Однако у более высокопрочных сталей допускаемое напряжение сильнее уменьшается сростом концентрации напряжений. Это приводит к выравниванию Rv у всех сталей при высокой концентрации напряжений. Поэтому приведенные в табл. 5 значения Rv для групп с 3-й до 8-й одинаковы для всех марок стали. Для 1-й и 2-й групп значения Rv у высокопрочных сталей выше, чем приведенные в табл. 5 для стали ВСтЗсп. Отсюда следует, что применение высокопрочных сталей при работе на выносливость целесообразно только при устранении в конструкции острых концентраторов. Наиболее нагруженное сечение проектируемой в работе стержневой конструкции расположено вблизи места ее прикрепления к стенке. Прикрепление лобовыми угловыми швами соответствует 6 группе (см.табл.5), следовательно Rv=45 МПа. Коэффициент α в формуле (3) зависит от числа циклов n и рассчитывается по формулам: при n≥3,9·106 α = 0,77 для всех групп; при n<3,9·106 для 1-й и 2-й групп α = 0,064(n/106)2 - 0,5(n/106) + 1,75; для групп c 3-й по 8-ю α = 0,07(n/106)2 - 0,64(n/106) + 2,2. Например, для 6-й группы, при n=106, α = 1,63. Коэффициент γv отражает зависимость допускаемых напряжений от показателя асимметрии цикла ρ, равного отношению минимального напряжения за цикл к максимальному, т. е. а также от знака напряжений. Растяжение способствует, а сжатие препятствует возникновению трещин, поэтому значение γv при одинаковых ρ зависит от знака σmax. Влияние ρ на допускаемое напряжение связано главным образом с тем, что число циклов до появления усталостной трещины зависит от размаха напряжений (σmax - σmin). Поэтому при одинаковых значениях действующего в сечении максимального напряжения σmax число циклов до разрушения различно в зависимости от σmin. Соответствующую поправку в расчет вносит коэффициент γv: при сжатии ( σmax < 0) γv = 2 / (1 - ρ); при растяжении, чередующимся со сжатием (σmax > 0,σmin < 0; 1≤ρ≤0), γv = 2,5 / (1,5 - ρ); при знакопостоянном растяжении ( σmax > σmin > 0, 0≤ ρ ≤0.8) γv = 2/(1,2 - ρ); при малом изменении растягивающей нагрузки (σmin→σmax>0; 0,8≤ρ≤1) γv = 1/(1 - ρ). В случае пульсирующего нагружения, когда σmin = 0, ρ = 0, при сжатии γv = 2, при растяжении γv = 1,67. При ρ→1 γv → [σ] =Ry . (4) Значение расчетного сопротивления Ry по пределу текучести определяют по формуле Ry =σТ/γm , где γm - коэффициент надежности по материалу. Для ВСтЗсп σТ= 250 МПа, γm = 1,05 , Ry = 238 МПа. При статическом сжатии допускаемое напряжение снижают в связи с опасностью потери устойчивости: [σ] =Ry·φ . (5) где 0<φ≤1. Коэффициент φ зависит от гибкости и относительного эксцентриситета. Его точное значение может быть найдено только после определения размеров сечения. Для ориентировочного выбора Aтр по формуле следует задаться значением φ. При небольшом эксцентриситете приложения нагрузки можно принять φ=0,6. Такой коэффициент означает, что прочность стержня при сжатии из-за потери устойчивости снижается до 60% от прочности при растяжении. Если при центральном сжатии φ<0,5 , то сечение выбрано неудачно. Значения φ>0,9 редко удается получить в связи с ограничениями на габаритные размеры сечения. В случае переменной сжимающей нагрузки [σ] следует выбирать равным меньшему из двух значений, получаемых из условия усталостной прочности (3) и из условия устойчивости (5), а при переменной растягивающей нагрузке из условий (3) и (4). Вычисленную по формуле (2) площадь требуемого сечения необходимо разделить на число ветвей и подобрать по справочнику ближайший по площади сечения стандартный профиль. Далее необходимо провести проверку на прочность (см. раздел 5), поскольку при выборе сечения была учтена только продольная сила, а изгибающий момент не был учтен. Нужна также проверка на устойчивость (см. раздел 6), поскольку точное значение коэффициента φ можно определить только после выбора всех размеров сечения. В результате этих проверок приходится корректировать выбор размеров сечения, чтобы обеспечить прочность и устойчивость с минимальным запасом, то есть получить рациональное конструктивное решение. Число попыток зависит от правильности выбора Aтр. При изгибе можно получить более удачное значение Aтр, если при расчете внести поправку с учетом эксцентриситетов. Поскольку напряжения от растяжения и изгиба складываются, то суммарное напряжение σ=σp+σMx+σMy=σ(1+mx+my), где mx и my - относительные эксцентриситеты (см. п. 1), в связи с чем значение позволит сделать более удачный выбор площади сечения стойки. Для снижения массы конструкции следует увеличивать габаритные размеры сечения (но не выше максимальных, приведенных в задании hmax и bmax). При этом растут момент сопротивления изгибу и коэффициент φ. Особенно выгодно раздвигать ветви составного сечения, так как при этом W и φ повышаются, а масса конструкции растет только за счет соединительных элементов между ветвями. Если сечение сплошное (например, коробчатое) то наилучшим при работе на устойчивость и изгиб будет сечение с минимальной толщиной стенок и максимальными габаритами. Однако толщина стенок не должна быть слишком малой, так как возможны проблемы с местной устойчивостью тонких листов (см. раздел 8). Выбор стали с более высоким пределом текучести дает заметное снижение массы только при малой гибкости конструкции (при φ>0,6), так как при большей гибкости коэффициент φ снижается по мере ростаRy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||